用表存储代替递归算法

我们知道递归算法非常低效，低效的原因在于递归的过程会产生冗余计算。

拿我们熟悉的斐波那契数列为例，计算公式为：F(n) = F(n - 1) + F(n - 2)，其中F(0) = F(1) = 1。

例如计算F(5)的执行过程：

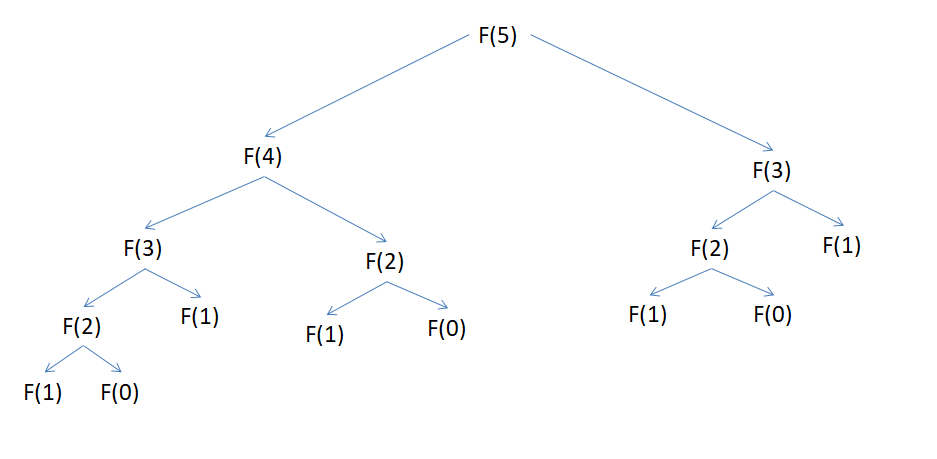
在此过程中，F(4) 执行了1次；F(3)执行了2次；F(2)执行了3次；F(1)执行了5次；F(0)执行了3次;由此可见，递归算法低效的原因。

为了提高执行效率，通常可以用一个表来代替递归，例如 C++ 中的vector。

这里举两个例子，分别以递归和非递归两种方式实现：

问题一：菲波那切数列

第一种方法：递归实现

int fib(int n)
{
    if(n <= 1)
        return 1;

    return fib(n - 1) + fib(n - 2);
}

第二种方法：非递归实现——用表代替递归

int fibona(int n)
{
    if(n <= 1)
        return 1;

    vector<int> aNumber(n + 1,0);
    aNumber[0] = 1;
    aNumber[1] = 1;
    for (int i = 2;i <= n;i++)
    {
        aNumber[i] =  aNumber[i - 1] + aNumber[i - 2];
    }

    return aNumber[n];
}

问题二：计算数学公式

算法实现此公式：

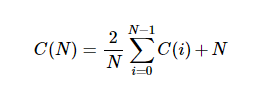
第一种方法：递归实现

float eval1(int n)
{
    if(n == 0)
        return 1;

    float sum = 0;
    for (int i = 0; i < n;i++)
        sum += eval1(i);
    return 2 * sum / n + n;
}

 

第二种方法：非递归实现——用表代替递归

1. 复杂度是O(N * N)

float eval2(int n)
{
    vector<float> aNumber(n + 1,0);
    aNumber[0] = 1;

    for (int i = 1; i <= n;i++)
    {
        float fSum = 0;
        for (int j = 0; j < i;j++)
        {
            fSum += aNumber[j];
        }
        aNumber[i] = 2 * fSum/i + i;
    }

    return aNumber[n];
}

2. 最完美的方案， 复杂度是O(N)

float eval3(int n)
{
    vector<int> aNumber(n + 1,0);
    aNumber[0] = 1;

    float fSum = 0;
    for (int i = 1;i <= n;i++)
    {
        fSum += aNumber[i - 1];
        aNumber[i] = 2 * fSum/i + i;
    }

    return aNumber[n];
}