数据结构之栈

一、栈的特点

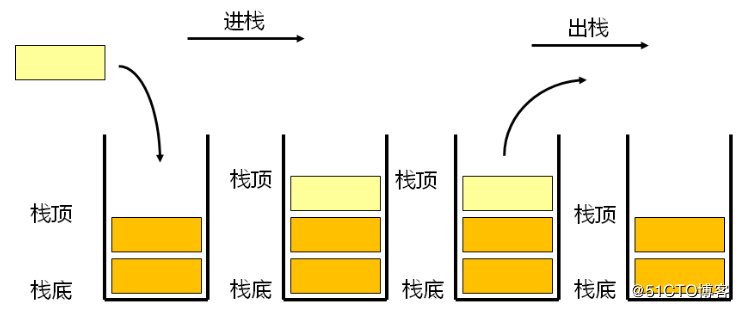
（1）栈是一种线性结构，栈中的元素遵循先入后出的原则，最先进入的元素所在位置叫做栈底，最后放入的元素所在位置叫做栈顶。

这种结构类似于盛放羽毛球的圆筒，一端封闭，另一端开口，先放入的羽毛球位于筒的底部（即栈底），后放入的羽毛球位于筒的入口（即栈顶）。

（2）栈也是一种抽象的逻辑结构，依赖于物理结构（如数组、链表）而存在。既可以使用数组实现，也可以使用链表实现。

（3）出栈、入栈的时间复杂都是O(1)。

 

 

二、 栈的基本操作

栈的基本操作主要是出栈、入栈、获取栈顶元素等。

（1）入栈

栈的入栈操作只允许从栈顶一侧放入新元素，放入的新元素成为新的栈顶。

（2） 出栈

栈的出栈操作只允许从栈顶弹出，出栈元素的前一个元素变成了新的栈顶。

 

三、基于数组实现栈

 

#include <iostream>
#include <assert.h>

// 基于数组实现的栈(模板类)
template <class T>
class ArrayStack
{
public :
    ArrayStack(int nCapcity = 8);
    ~ArrayStack();

    bool Push(const T& ele);
    T    Pop();
    T&   GetPop();
    int  GetNum();

private:
    void Resize();
private:
    T*   m_pElement;
    int  m_nCapicity;
    int  m_nNum;
};

template<class T>
ArrayStack<T>::ArrayStack(int nCapcity)
    :m_nCapicity(nCapcity)
    ,m_pElement(new T[nCapcity])
    ,m_nNum(0)
{

}

template<class T>
ArrayStack<T>::~ArrayStack()
{
    delete[] m_pElement;
}

template<class T>
bool ArrayStack<T>::Push(const T& ele)
{
    if(m_pElement == NULL)
    {
        printf(" m_pElement == NUL \n");
        assert(false && "m_pElement == NUL");
        return false;
    }
    if(m_nNum >= m_nCapicity)
    {
        Resize();
    }

    m_pElement[m_nNum] = ele;
    m_nNum++;
    return true;
}

template<class T>
T ArrayStack<T>::Pop()
{
    if(m_nNum <= 0)
    {
        return NULL;
    }

    m_nNum--;
    return m_pElement[m_nNum];
}

template<class T>
T& ArrayStack<T>::GetPop()
{
    if(m_nNum <= 0)
    {
        return NULL;
    }

    return m_pElement[m_nNum - 1];
}

template<class T>
int ArrayStack<T>::GetNum()
{
    return m_nNum;
}

template<class T>
void ArrayStack<T>::Resize()
{
    if(NULL == m_pElement)
    {
        if(m_nCapicity == 0)
        {
            m_nCapicity = 8;
        }
        m_pElement = new T[m_nCapicity];
        return;
    }

    T* pNewEle = new T[m_nCapicity * 2];
    for(int i = 0;i < m_nNum;i++)
    {
        pNewEle[i] = m_pElement[i];
    }

    delete[] m_pElement;
    m_pElement = pNewEle;
    m_nCapicity = m_nCapicity * 2;
}

int main()
{
    printf("Welcome to stack! \n");

    ArrayStack<int> stackVal1(4);
    stackVal1.Push(1);
    stackVal1.Push(10);
    stackVal1.Push(20);
    stackVal1.Push(40);
    stackVal1.Push(60);

    int nNum = stackVal1.GetNum();
    printf("------num:%d \n",nNum);
   
    for(int i = 0;i < nNum;i++)
    {
        int val1 = stackVal1.Pop();
        printf("%d  ",val1);
    }
    printf("\n");

    nNum = stackVal1.GetNum();
    printf("------num:%d \n",nNum);
    return 0;
}

 

四、基于链表实现栈

#include <iostream>
#include <assert.h>

template<class T>
class Node
{
public:
    Node():m_pNext(NULL){}
    Node(T& data):m_Data(data),m_pNext(NULL){}
    Node(T& data,Node<T>* pNext):m_Data(data),m_pNext(pNext){}
public:
    T        m_Data;
    Node<T>* m_pNext;
};

//单链表
template<class T>
class SingleList
{
public:
    SingleList():m_pHead(NULL),m_pCurrent(NULL),m_nSize(0){}
    ~SingleList()
    {
        Clear();
    }

    //获取链表元素个数
    int GetNum()
    {
        return m_nSize;
    }

    //尾部插入新节点
    bool InsertNode(const T& data)
    {
        Node<T>* pNew = new Node<T>();
        pNew->m_Data = data;
        pNew->m_pNext = NULL;
        if(m_pHead == NULL)
        {
            m_pHead = pNew;
            m_pCurrent = pNew;
        }
        else
        {
            m_pCurrent->m_pNext = pNew;
            m_pCurrent = pNew;
        }
        m_nSize++;
        return true;
    }

    //删除节点
    int DeleteNode()
    {
        if(m_nSize == 0 || m_pHead == NULL|| NULL == m_pCurrent)
        {
            return -1;
        }

        if(m_pHead == m_pCurrent)
        {
            m_pHead = m_pCurrent->m_pNext;
            delete m_pCurrent;
            m_pCurrent = m_pHead;
        }
        else
        {
            Node<T>* pCurrent = m_pHead;
            while(pCurrent)
            {
                if(pCurrent->m_pNext == m_pCurrent)
                {
                    pCurrent->m_pNext = m_pCurrent->m_pNext;
                    delete m_pCurrent;
                    m_pCurrent = pCurrent;
                    break;
                }
                else
                {
                    pCurrent = pCurrent->m_pNext;
                }
            }
        }
       
        m_nSize--;
        return m_nSize;
    }

    //获取当前节点数据
    void GetCurrentNodeData(T& data)
    {
        if(m_pCurrent)
        {
           data = m_pCurrent->m_Data ;
        }
    }

    //设置当前节点数据
    void SetCurrentNodeData(T& data)
    {
        if(m_pCurrent)
        {
            m_pCurrent->m_Data = data;
        }
    }

    //清空列表
    void Clear()
    {
        if(m_nSize == 0 || m_pHead == NULL)
        {
            return;
        }

        Node<T>* tepCurrent = m_pHead;
        Node<T>* tepNext = m_pHead->m_pNext;
        
        while(tepCurrent)
        {
            delete tepCurrent;
            tepCurrent = tepNext;
            if(tepNext)
            {
                tepNext = tepNext->m_pNext;
            }
        }
        m_pHead = NULL;
        m_pCurrent = NULL;
        m_nSize = 0;
    }
private:
    Node<T>*        m_pHead;
    Node<T>*        m_pCurrent;
    int             m_nSize;
};

template<class T>
class LinkStack
{
public:
    LinkStack(){}
    ~LinkStack(){}
    //获取元素个数
    int  GetNum()
    {
        return m_SingleList.GetNum();
    }

    //添加新元素
    bool Push(const T& data)
    {
        return m_SingleList.InsertNode(data);
    }

    //移除栈顶元素
    T    Pop()
    {
        T temp;
        if(GetNum() <= 0)
        {
            return -1;
        }
        m_SingleList.GetCurrentNodeData(temp);
        m_SingleList.DeleteNode();
        return temp;
    }
private:
    SingleList<T> m_SingleList;
};

int main()
{
    printf("Welcome to link stack.\n");
    LinkStack<int> stackVal2;
    stackVal2.Push(100);
    stackVal2.Push(200);
    stackVal2.Push(300);
    stackVal2.Push(500);

    int nNum = stackVal2.GetNum();
    for(int i = 0;i < nNum;i++)
    {
        int val = stackVal2.Pop();
        printf("Pop:%d  =================\n",val);
    }
    

    return 0;
}