leedcode 84. 柱状图中最大的矩形(单调栈)
题目描述
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:
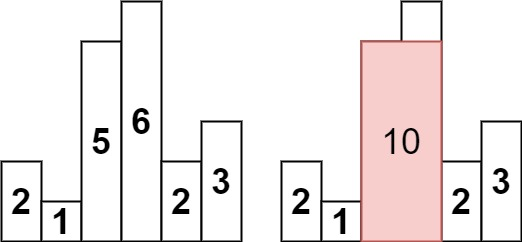
输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10
示例 2:
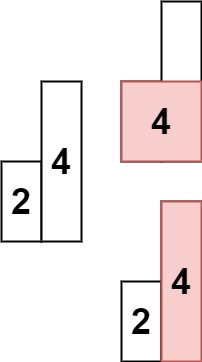
输入: heights = [2,4]
输出: 4
提示:
1 <= heights.length <=105
0 <= heights[i] <= 104
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/largest-rectangle-in-histogram
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题解
- 暴力解法就是一列列矩阵遍历,看看以 当前矩阵的高度 作为高度,向左最远能到哪里,最右能到哪里。再对此解法进行优化,只是一道 单调栈 应用的典型例题。利用单调栈可以很快捷地找到 以 当前矩阵的高度 作为高度,向左最远能到哪里,最右能到哪里,就不用每次都重复一遍遍找了。
class Solution {
public:
int largestRectangleArea(vector& heights) {
int n=heights.size();
int ans=0;
int i=0;
stacks;//单调栈中 自底向上 高度依次递增
while(iheights[i]){//如果当前高度比栈顶对应的高度高
int x=s.top();//栈顶值
s.pop();
if(!s.empty()){
ans=max(ans,heights[x]*(i-s.top()-1));//向左最远能到s.top() 最左是到i
}else{
ans=max(ans,heights[x]*i);//如果栈中没有别的值了 那么向左最远到0
}
}
s.push(i);
i++;
}
while(!s.empty()){//遍历完毕 依次弹出栈中所剩的值
int x=s.top();
s.pop();
if(!s.empty()){//处理操作同上
ans=max(ans,heights[x]*(i-s.top()-1));
}else{
ans=max(ans,heights[x]*i);
}
}
return ans;
}
};代码有点冗余,因为遍历完毕后,栈中还有剩下的值。如何才能没有值剩下呢?那就是一开始就在末尾放入一个高度为0的矩阵。
class Solution {
public:
int largestRectangleArea(vector& heights) {
heights.push_back(0);//一开始就在末尾放入一个高度为0的矩阵
int n=heights.size();
int ans=0;
int i=0;
stacks;//单调栈中 自底向上 高度依次递增
while(iheights[i]){//如果当前高度比栈顶对应的高度高
int x=s.top();//栈顶值
s.pop();
if(!s.empty()){
ans=max(ans,heights[x]*(i-s.top()-1));//向左最远能到s.top() 最左是到i
}else{
ans=max(ans,heights[x]*i);//如果栈中没有别的值了 那么向左最远到0
}
}
s.push(i);
i++;
}
return ans;
}
};但是这种方法代码写的还是不够简洁,还有更简单的思想,简洁地代码见例题:

