卡特兰数
一分钟数学——卡特兰数(上)
long long n,f[maxn]; int main() { cin>>n; f[1]=1; for(int i=2;i<=n;i++) f[i]=f[i-1]*(4*i-2)/(i+1); cout<<f[n]; return 0; }
卡特兰数
生活中有很多有关卡特兰(Catalan,人名,1814~1894)数的问题,有一本书就讲了将近200个“卡特兰数”问题。我们来看几道题,请大家先试试看,并找找相似之处。
一、切割三角形
把一个凸五边形分割成若干个的三角形(必须全都是三角形),一共有几种方法?如果是凸N边形呢?
二、小卖部买水
春游啦,中午时分,烈日当空,同学们都很口渴,于是大家拿着钱来到小卖部买水。店主看了一下,一共有8名同学,其中4个人只有1元,另外4个人只有2元(不可以分成2个1元的)。已知一瓶水1元,店主又没有准备零钱,请问:为了能够让所有人都买到水,且店主只用手中已有的钱找零,有多少种排队买水的方法?(假设所有人都是一样的,只能依靠手里有的钱的多少来区分)
三、算式添括号
每个左括号‘(’必须有一个右括号‘)’匹配,且整个算式能够正常计算。例如一个算式是:2+1×4-3÷5,问括号有多少种不同的添法?(不考虑算式的计算结果以及过程)
四、最短路线问题
一个5×5的网格,走最短路线,不得超过对角线,问有多少种不同的走法?(从左下角至右上角)
这四个问题的本身都是和卡特兰数有关的,它们有什么共同点?卡特兰数究竟是什么呢?还能举出哪些类似的例子呢?我们下期再讲。
一分钟数学——卡特兰数(中)
卡特兰数
这次我们主要讲上期的解答(点击此处→→卡特兰数←←查看上期图文内容)。
把一个凸六边形分割成若干个的三角形(必须全都是三角形),一共有几种方法?如果是凸N边形呢?
下图是将正六边形切割成若干个三角形的全部方法
卡特兰数是有递归(←←点此查看 一分钟算法——递归 的内容)的思想的,将凸六边形的六个点都标上编号V1到V6,随后我们要以V1和V6为三角形的底边找出另外一个顶点Vk,来组成一个三角形。这个k是从2到5的,每一种对应的就是左半部分和右半部分分别的情况数,这同样都是凸多边形,所以可以是递归。把左右两边的情况数相乘,因为是乘法原理,就可以得到k的一个结果,将所有k的结果相加即可。设F(N)为凸N边形分割成三角形的情况数,列出的递归关系式就是:F(N)=F(0)*F(N-1)+F(1)*F(N-2)+……+F(N-1)*F(0)。
卡特兰数是组合数学中常见也是重要的特殊计数公式。
首先给出一个现实问题的模型:
给出凸多边形的边数n,求解该凸多边形内部不相交的对角线把这个区域分成三角形区域的方法数。

首先我们进行初步的分析,当n=2,h2=1,也就是说对于三角形,划分的情况数是1.这似乎有些不好理解,由于三角形内部无法添加对角线,所以符合情况的就是三角形本身,情况数为1.
下面我们讨论n取任意值的情况。
看下面的图。
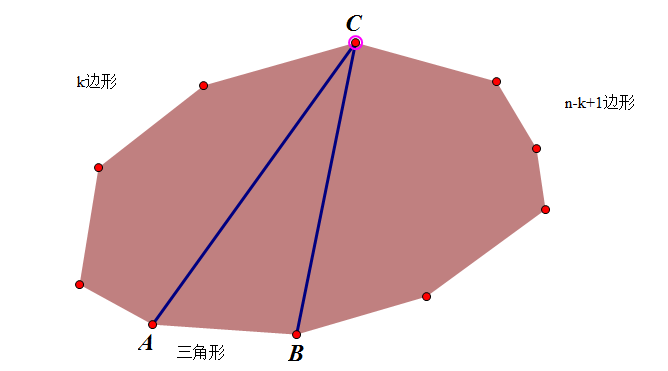
考虑将n+1凸边形的子问题,即我们将AB视为基边,枚举C的位置,有n-1个可枚举位置,然后结合基本的计数原理,我们能够看到下面的递推式能够不重不漏的表示出h[n].
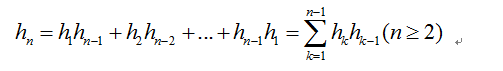
那么对于其它三道题来说,都是同一种类型的,就是走网格(也就是第四题)。买水的可以看作在每个时刻,有一元钱的必须不少于有两元钱的。添括号的同样,就是左括号和右括号而已。
下图是5×5的网格的最短路径(不超过对角线)的所有情况
在x-y坐标平面上,考虑两种一格一格的移动,每一次平移我们可以上移一格,也可以下移一格,左移或者右移也是一样。姑且这样定义:
右移U: (X,Y)——。(x+1,y) 上移U: (X,Y)——>(x,y+1)
现在问通过这两种移动每次移动一次,有多少种方法可以从点(0,0)移动到点(5,5),这显然是5个R和5个U的组合排列,共十次移动,10选5就可以了,C(10,5)
比如: RRUURRURUU 是符合要求的
我们再加点限制,在这个过程中不可越过直线y=x,但可接触。于是你该知道,这样的限制意味着,移动到每一点时,所经过的R的个数一定大于或等于U的个数,如果小于则不合要求。
比如: RRUURRURUU 符合限制条件
比如: RUUURRRUUR 就是不和限制条件
对于不符合限制条件的情形来说,我们先把它在第一次越过y=x点处断开,分为两个部分
RUU URRRUUR
然后第一部分因为符合要求不变,第二部分做翻转操作,即R变U,U变R,于是得
RUR RUUURRU
其实这样的分法,我们可以想到,在第一次越过直线时分开,即会导致前面部分得U比R多一个,而后面部分的R会比U多一个,一翻转就是U比R多一个,如此,总共翻转序列后U就比R多出两个,比如此处R只有4个U却有5个。同样的道理,可知所有不满足条件的情形一一对应着4个R和6个U的排列情形,这些情况的个数就是10选4么,C(10,4),现在你知道了,加上限制条件后方法数就是
N=C(10,5)-C(10,4)=45
于是,可以这样总结,对于任意正整数n,如果你想从点(0,0)移动到点(n,n)且不越过直线y=x的方法数为:
Kn=C(2n,n)-C(2n,n-1)
这个Kn就是传说中的卡特兰数,简单吧~~ K0=1,K1=1,K2=2,K3=5,K4=14,K5=42,K6=132
那如何计算总方案数呢?如上图,把它看作是在一个坐标系上的,从(0,0)点到(N,N)点。画出对角线(直线y=x,表示x轴上的坐标和y轴上的坐标相等),思路就是用总的方案数(无限制条件)减去超过对角线的。总方案数就是一共走2N条边,其中N条向上,N条向右,就是从2N中选N个。如果超过对角线,设为到达点P,然后观察一下每一个过对角线一格(同点P一样)的点,发现它们都在直线y=x+1上。这样就可以把超出对角线的路径沿直线y=x+1进行映射,得到一条新的路径,是从A'(-1,1)到B(N,N)。而我们发现,任何一条从A'(-1,1)到B(N,N)的路径必然都会经过直线y=x+1,也就可以得到一条映射回去的过直线y=x的路径。来求从A'(-1,1)到B(N,N)的路径数,也是2N条边,不过是N-1条向上的,N+1条向右的,因此是从2N里选N-1,或是2N里选N+1。总数就是C(2N,N)-C(2N,N-1)。这种问题也称为Dyck Path,其实这个最短路径的最终结果和之前的递归结果是相同的,只是推导过程很复杂,这里就不细说了。
再说说二叉树(←←点击查看 一分钟算法——二叉树 的内容)吧,有N个点,分布在二叉树上,问有多少种不同的放法?(不规定是完全二叉树)也是和卡特兰数有关的哦,想想上述几个例子到底为什么和卡特兰数有关呢?这是一个怎样的序列呢?敬请期待下期!
一分钟数学——卡特兰数(下)
卡特兰数
根据我们之前推出的卡特兰数的递归关系式F(N)=F(0)*F(N-1)+F(1)*F(N-2)+……+F(N-1)*F(0),或是组合算式 C(2N,N)-C(2N,N-1),就可以很容易地得到前几个卡特兰数。不过,这里要注意的是,我们并不一定通过这两种形式得到的是第N个卡特兰数,有可能需要进行细微的改动,或许是N -1,这里就不细说了。那么前几项就是:1、1、2、5、14、42、132、429、1430、4862、16796、58786、208012、742900、2674440、9694845、35357670、129644790、477638700、1767263190、6564120420、24466267020、91482563640……
由此可见,卡特兰数,又称卡特兰数列,和斐波那契数列一样,数增长得很快,一开始的几项还很小,但是不一会儿就大了很多。而由之前的组合算式 C(2N,N)-C(2N,N-1),我们可以推出一个卡特兰数列的通项公式:
现在来介绍一下卡特兰数的发展过程。1751年,欧拉在于与哥德巴赫的通信中提到了众所周知(不过是现在)的切割三角形问题。可是,欧拉并没有提到有关卡特兰数的信息,而是给出了这道题的一个非常非常复杂的解,尽管它还是能够转化成卡特兰数。
1758年,Johann Segner 给出了欧拉问题的递归关系式,也就是我们之前说的。1838年,越来越多的数学爱好者开始关注这个热门话题,掀起了一股热潮。Gabriel Lame 给出了完整证明和简洁表达式,Eugene Charles Catalan 在研究汉诺塔时探讨了相关问题,解决了括号表达式的问题(之前也讲过)……直到1900年,Eugen Netto 在著作中将该数列归功于Catalan。不过,1988年以及1999年的文献研究表明实际上最早发现Catalan数的并不是欧拉,而是1730年中国清朝时期的明安图(蒙古人),《割圆密率捷法》被他的学生在1774年完成发表。
卡特兰数是我们数学领域中较晚的一个发现,像什么幻方、海伦公式,还有斐波那契数列,都是一两千年前的事情。卡特兰数却是在18世纪至20世纪的,可是计算机领域就更不同了,被称为计算机之父的图灵在20世纪40年代提出了许多计算机的理论,第一台计算机是冯诺依曼——发明了归并排序的人——在20世纪中期发明的。
三、卡特兰数的应用
1.给乘积X1X,X3......Xn加括号的方法数
将问题转化一下,就是爬坐标,左括号数一定要大于或者等于右括号数
2.排列三个1和三个-1,使得从左到右部分和总是非负的方法数
将问题转化一下,就是加括号的方法数,排1的个数一定要大于或者等于排的-1个数
3.给定四个1和四个0,进行排列组合,使得从左往右读0的个数不超过1的个数
将问题转化为读括号,从左往右读,左括号一定要大于或等于右括号个数。
4.来个看起来复杂点的:将1 2 3 4 5 6排成两行,使得每行3个数,并且每行从左往右读值增加,每一列小数在上
我们可以想象, 1 2 3代表左括号, 4 5 6代表右括号,为了从左往右读值增加,方法会有很多,但加上小数在上大数在下,就相当于左括号数总是大于或者等于右括号数么。假设这里的“左括号”少一个,那么下面一行对应会多一个左括号,而且因为值要求从小到大排列,即每行左括号总是在前,那么在上下对齐时,由于下面左括号要多,所以下行最后一个左括号肯定对齐着上行的右括号,是不符合要求的,但上面行的左括号要多这是没问题的。
5【阿里巴巴笔试题】:说16个人按顺序去买烧饼,其中8个人每人身上只有一张5块钱,另外8个人每人身上只有一张10块钱。烧饼5块一个,开始时烧饼店老板身上没有钱。16个顾客互相不通气,每人只买一个。问这16个人共有多少种排列方法能避免找不开钱的情况出现。
将问题转化为:带5块钱的排前面的个数总是要大于带10块钱的人的个数,即C(16,8)-C(16,7)
6.【腾讯笔试题】在图书馆一共6个人在排队,3个还《面试宝典》一书,3个在借《面试宝典》一书,图书馆此时没有了面试宝典了,求他们排队的总数?
将问题转化为:还书的人总是要大于或等于借书的人,即C(6,3)-C(6,2)
7.出栈次序问题
一个栈(无穷大)的进栈序列为1,2,3,..n,有多少个不同的出栈序列?
将问题转化为:入栈的数的个数总是要大于或者等于出栈数的个数。C(2n,n)-C(2n,n-1)
8【阿里巴巴笔试题】12个高矮不同的人,排成两排,每排必须是从矮到高排列,而且第二排比对应的第一排的人高,问排列方式有多少种?
C(12,6)-C(12,5)


