求数组的所有子数组的和的最大值

题目描述：

输入一个整形数组，数组里有正数也有负数。 数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。 求所有子数组的和的最大值。要求时间复杂度为O(n)。

例如输入的数组为8,-4,6,-1,3,7,2,-3，和最大的子数组为8,-4,6,-1,3,7,2， 因此输出为该子数组的和21。

思路分析：

求一个数组的最大子数组和，如输入的数组为8,-4,6,-1,3,7,2,-3。由于要考虑到时间复杂度，即要尽量减少for的循环遍历次数，我和丹丹讨论了一下，想到了时间复杂度

为O(n)的算法如下：

#include<iostream.h>
int maxsum(int*a,int n)
{
	int sum=0;
	int c=0;
	for(int i=0;i<n;i++)
	{
		if(c<0)
			c=a[i];
		else
			c+=a[i];
		if(sum<c)
			sum=c;
	}
	return sum;
}
int main()
{
	int a[8]={8,-4,6,-1,3,7,2,-3};
	cout<<maxsum(a,8)<<endl;
	return 0;
}

　　

运行结果如下：

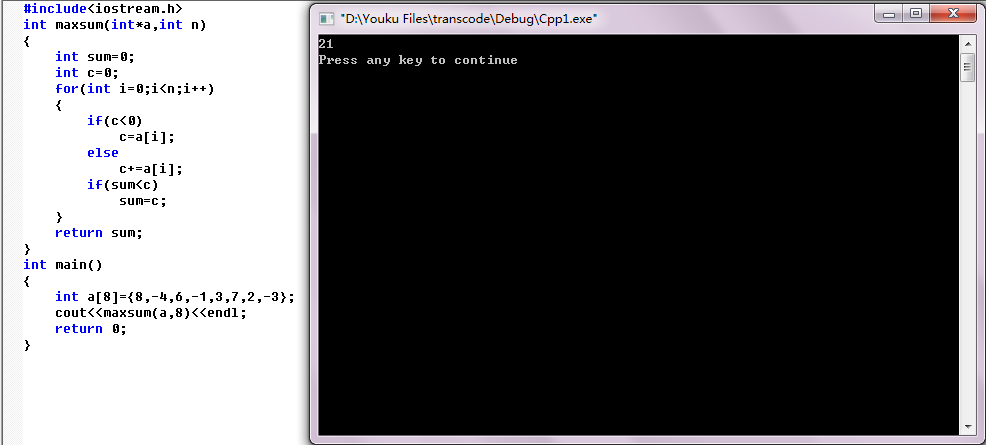
考虑到数组全是负数的情况，我和丹丹又对程序做了一些改变：

#include <iostream.h>     
#define n 8 
int maxsum(int a[n])      
{    
int max=a[0];       //如果是全负情况，返回最大数     
int sum=0;    
for(int i=0;i<n;i++)    
{    
    if(sum>=0)     //如果加上某个元素，sum>=0的话，就加     
       sum+=a[i];    
   else       
      sum=a[i];  //如果加上某个元素，sum<0了，就不加     
    if(sum>max)    
         max=sum;    
  }    
   return max;    
}       
int main()    
{    
   int a[]={-8,-4,-6,-1,-5,-7,-2,-3};    
   cout<<maxsum(a)<<endl;    
   return 0;    
}    

运行结果：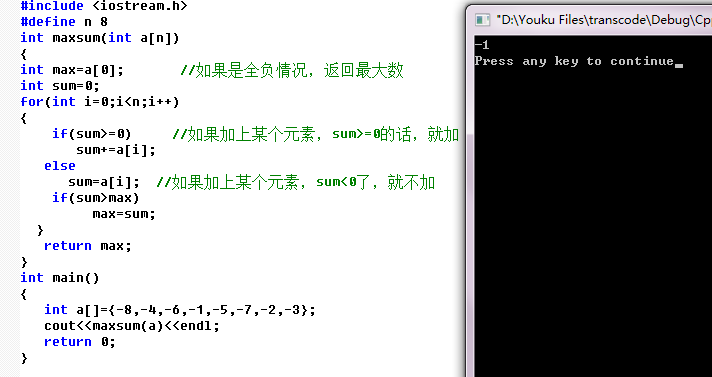

以上是我们对求数组的所有子数组的和的最大值程序设计的探讨。