GNSS学习笔记-坐标转换

GNSS 坐标转换

GNSS计算主要涉及三个坐标系，地心地固坐标系，地理坐标系和站心坐标系。这里主要介绍一下三个坐标的含义和转换公式。

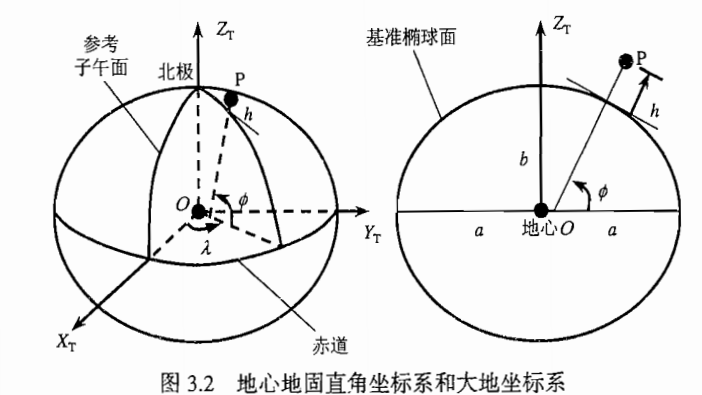
• 地心地固坐标系如图X,Y,Z表示 (ECEF坐标系)，以地心O为坐标原点，Z轴指向协议地球北极，X轴指向参考子午面与地球赤道的交点，也叫地球坐标系。一般GNSS坐标计算都在地心地固坐标系下进行的。由于地球是椭圆形，有WGS-84和CGC2000等多种标准

• 地理坐标系则通过经度(longitude)，纬度(latitude)和高度(altitude)来表示地球的位置，也叫经纬高坐标系(LLA坐标系)。

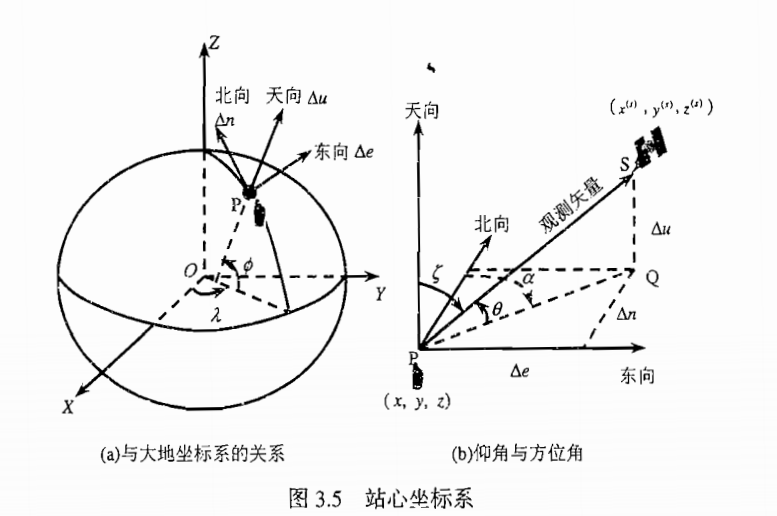
• 站心坐标系以用户所在位置P为坐标原点，三个轴分别指向东向，北向和天向，也叫东北天坐标系(enu坐标系)。站心坐标系的天向方向和地理坐标系的高度方向是一致的。站心坐标系用在惯性导航和卫星俯仰角计算中较多。

参数	WGS-84	CGC200
基准椭球体的长半径a	6378137.0 m	6378137.0 m
基准椭球体的极扁率f	1/298.257223565	1/298.257223563
地球自转角速度We	7.2921151467*1e-5	7.2921151467*1e-5
地球引力和地球质量的乘积GM	3986004.418*1e8	3986004.418*1e8
光速	2.99792458*1e8 m/s	2.99792458*1e8 m/s

LLA坐标系转ECEF坐标系

LLA坐标系下的(lon,lat,alt)转换为ECEF坐标系下点(X,Y,Z)

$$\begin{cases} X=(N+alt)cos(lat)cos(lon)\\ Y=(N+alt)cos(lat)sin(lon)\\ Z=(N(1-e^2)+alt)sin(lat) \end{cases}$$

其中e为椭球偏心率，N为基准椭球体的曲率半径

$$\begin{cases} e^2=\frac{a^2-b^2}{a^2}\\ N=\frac{a}{\sqrt{1-e^2sin^2lat}} \end{cases}$$

由于WGS-84下极扁率$f=\frac{a-b}{a}$,偏心率e和极扁率f之间的关系：

$$e^2=f(2-f)$$

坐标转换公式也可以为

$$\begin{cases} X=(N+alt)cos(lat)cos(lon)\\ Y=(N+alt)cos(lat)sin(lon)\\ Z=(N(1-f)^2+alt)sin(lat) \end{cases}$$

$$N=\frac{a}{\sqrt{1-f(2-f)sin^2lat}}$$

python实现

def lla2ecef(lat,lon,alt):
    WGS84_A = 6378137.0
    WGS84_f = 1/298.257223565
    WGS84_E2 = WGS84_f*(2-WGS84_f)
    deg2rad = math.pi/180.0
    rad2deg = 180.0/math.pi
    lat *= deg2rad
    lon *= deg2rad
    N = WGS84_A/(math.sqrt(1-WGS84_E2*math.sin(lat)*math.sin(lat)))
    x = (N+alt)*math.cos(lat)*math.cos(lon)
    y = (N+alt)*math.cos(lat)*math.sin(lon)
    z = (N*(1-WGS84_f)*(1-WGS84_f)+alt)*math.sin(lat)
    return [x,y,z]

ECEF坐标系转LLA坐标系

ECEF坐标系下点(X,Y,Z)转换为LLA坐标系下的(lon,lat,alt)

$$lon=arctan(\frac{y}{x})$$

$$alt=\frac{p}{cos(lat)-N}$$

$$lat=arctan\bigg[\frac{z}{p}\bigg(1-e^2\frac{N}{N+alt}\bigg)^{-1}\bigg]$$

$$p=\sqrt{x^2+y^2}$$

一开始lon是未知的，可以假设为0，经过几次迭代之后就能收敛

ECEF坐标系转enu坐标系

用户所在坐标点$P_0=(x_0,y_0,z_0)$,，计算点$P=(x,y,z)$在以点$P_{0}$为坐标原点的enu坐标系位置$(e,n,u)$这里需要用到LLA坐标系的数据，$P_0$的LLA坐标点为$LLA_0=(lon_0,lat_0,alt_0)$

$$\begin{gathered} \left[ \begin{array}{ccc} \Delta{x}\\\Delta{y}\\\Delta{z} \end{array} \right]= \left[ \begin{array}{ccc} x\\y\\z\end{array}\right]- \left[ \begin{array}{ccc} x_0\\y_0\\z_0\end{array}\right] \end{gathered}$$

$$\begin{gathered} \left[ \begin{array}{ccc} e\\n\\u \end{array} \right]=S\cdot \left[ \begin{array}{ccc} \Delta{x}\\\Delta{y}\\\Delta{z} \end{array} \right] \end{gathered}= \left[ \begin{array}{ccc} -sin(lon_0) & cos(lon_0) & 0 \\ -sin(lat_0)cos(lon_0) & -sin(lat_0)sin(lon_0) & cos(lat_0) \\ cos(lat_0)cos(lon_0) & cos(lat_0)sin(lon_0) & sin(lat_0) \end{array} \right]\cdot \left[ \begin{array}{ccc} \Delta{x}\\\Delta{y}\\\Delta{z} \end{array} \right]$$

即坐标变换矩阵$S=\left[ \begin{array}{ccc} -sin(lon_0) & cos(lon_0) & 0 \\ -sin(lat_0)cos(lon_0) & -sin(lat_0)sin(lon_0) & cos(lat_0) \\ cos(lat_0)cos(lon_0) & cos(lat_0)sin(lon_0) & sin(lat_0) \end{array} \right]$

enu坐标系转ECEF坐标系

$S$为单位正交矩阵

$$\mathbf{S}^{-1}=\mathbf{S}^\mathrm{T}$$

反之

$$\begin{gathered} \left[ \begin{array}{ccc} \Delta{x}\\\Delta{y}\\\Delta{z}\end{array} \right]=S^{-1}\cdot\left[ \begin{array}{ccc} e\\n\\u\end{array} \right]= \mathbf{S}^\mathrm{T}\cdot\left[ \begin{array}{ccc} e\\n\\u\end{array} \right] \end{gathered}$$

LLA坐标系转enu坐标系

上述可以看到，从LLA坐标系转换到enu坐标系有较多计算量，在考虑地球偏心率$e$很小的前提下，可以做一定的近似公式计算

$$\left[ \begin{array}{ccc} \Delta e\\ \Delta n \\ \Delta u \end{array} \right]= \left[\begin{array}{ccc} a\cdot cos(lat)\cdot \Delta lon & 0 & 0 \\ 0 & a \cdot \Delta lat & 0 \\ 0 & 0 & \Delta alt \end{array} \right]$$