游记 CSP2021-J1/S1

posted on 2021-09-19 22:34:52 | under 题解 | source

人在佛山，考场在南外。

学校信息队太强了，不仅租车还包午饭，点赞。

来写一下我做题经历吧：

S 组

官方答案：

ABACCCCBDACCCB
TFFTDC
TFFBCB
FTFBDD
DADCADADDC

阅卷的时候看到有个神秘分治（对我来说）和四毛子 RMQ，吓死了。然而这丝毫没有影响我看其他题，稍微看了一下，还是比较友好的。

8:30 准时开考。

选择题

  1. 没用过 Linux 爬了 显然（？）这个 ls 是 list 的缩写，A。
  2. 不就一加法，B。
  3. 调用函数是把一些信息压入栈里，递归就是把一大堆东西压进栈里再弹出来，所以 A。
  4. 堆排不稳定，因为遇到相等的元素时堆可能会让它们成为父子关系或者兄弟关系，这是你很难调整的（？），C。
  5. 首先记 \(maxk=a_1,mink=a_2\)，如果 \(maxk<mink\) 就交换。接着循环 \(i\in[2,n]\)，比较 \(a_i\) 和 \(a_{i+n}\)，较大者去和 \(maxk\) 比，较小者去和 \(mink\) 比。一共 \(1+3(n-1)=3n-2\) 次比较，C。
  6. 模拟一下，C。
  7. \(36=\frac{8\times 9}{2}\)，\(9\) 个点的完全图有 \(36\) 条边，但注意到是非联通图，多加一个点，C。
  8. 高度最小，完全二叉树，答案是 \(\left\lceil\log_2{2021}\right\rceil=11\)，B。
  9. 前序是根左右，中序是左根右，显然去掉左它们就一样了，C。
  10. 题意就是求逆序对，\(O(n^2)\) 数一下，A。
  11. 不难发现 \(\operatorname{solve}(t,n)\equiv 5^{t-1}\pmod{n}\)（记得 \(t-1\)，因为 if t=1 return 1），口算一下快速幂即可，累乘 \(base\) 的时候可以边模边乘，最后算出来 A。
  12. 可能很多人都知道是 \(O(F_n)\)，但选项没有。其实可以这样，把递推公式看成 \(F_n=2F_{n-1}\)，显然这个 \(F_n=2^{n-2}\)，是指数级，选 C。dsy 说还可以画树，这棵树像一颗满二叉树，所以 C。
  13. dp（？）设 \(f_{i,0/1}\) 表示第 \(i\) 个位置放/不放，那就有 \(f_{i,1}=f_{i-1,0}+1\)（还有一种前面全空的要加上），\(f_{i,0}=f_{i-1,0}+f_{i-1,1}\)，最后算出来 \(f_{8,0}+f_{8,1}=54\)，C。
  14. 算错了，不讲 补一下题解。
  15. 口算 SPFA，不断松弛即可，B。

时间过去了约 45 min。

然后是阅读程序。

阅读 T1

这个代码真的没看懂，尤其是这个 \(\arccos 0.5\)，是什么啊。
但不用慌，看到这个 \(t\) ，猜测输入的 \(a_1,b_1,c_1,a_2,b_2,c_2\) 是两个三维坐标点，\(t\) 就是它们的距离的平方。
那 \(d_1,d_2\) 是什么呢？观察到有个 t>=sp(d2+d1)，很像以前做 P3958 奶酪 时写的东西（所以要多刷题啊），猜测，\(d_1,d_2\) 是两个球的半径。

开题。

  1. 显然送分，欧几里得距离的平方显然是整数啊，T。
  2. 观察到 \(d_1^2-d_2^2+t\) 可能是奇数。如果先 \(\div \sqrt{t}\)，那么这个数就变成 double 类型了，再 \(\div 2\) 不会出事。但如果先 \(\div 2\)，那这个数就可能会被向下取整，就会算错，所以 F。
  3. 显然 F，sq 的参数类型是 int，传个 double 进去会出事。
  4. 可以手……

等一下，这个 \(\arccos 0.5\) 到底是什么，我们再来看一次代码。

if(t<=sq(d2-d1)) cout<<cu(min(d1,d2))*r*4;

如果两个球重叠，就输出 \(4\min(d_1,d_2)^3\arccos0.5\)，感觉似曾相识。
球的体积公式是 \(V_{\text{球}}=\frac{4}{3}r^3\pi\)，\(\min(d_1,d_2)^3\) 对应 \(r^3\)，\(4\) 对应 \(\frac{4}{3}\) 上面的 \(4\)，那 \(\arccos0.5\)……

就是 \(\frac{1}{3}\pi\)！

原来是两个球的体积啊，如果重叠输出较小的球的体积，如果不重叠输出 \(0\)，对，是球的体积并。

继续开题。

  1. 手算可得 T。
  2. 手算可得 D。
  3. 刚说了是 C。

这个阅读程序就做完了。

阅读 T2

并没有看懂在干什么，只会 23,25,26，还是说一下吧。

  1. \(n>0\) 时不可能执行，\(n\leq 0\) 时只会执行一次，F。
  2. 主定理一，\(O(n)\)。
  3. 主定理二，\(O(n\log n)\)，或者也可以理解成归并排序复杂度。

其他题全是蒙的。

update：stO dsy，原来是求最大子段和啊，wssb。

阅读 T3

一股 base 64 的味道，呕。

原理看这张图：

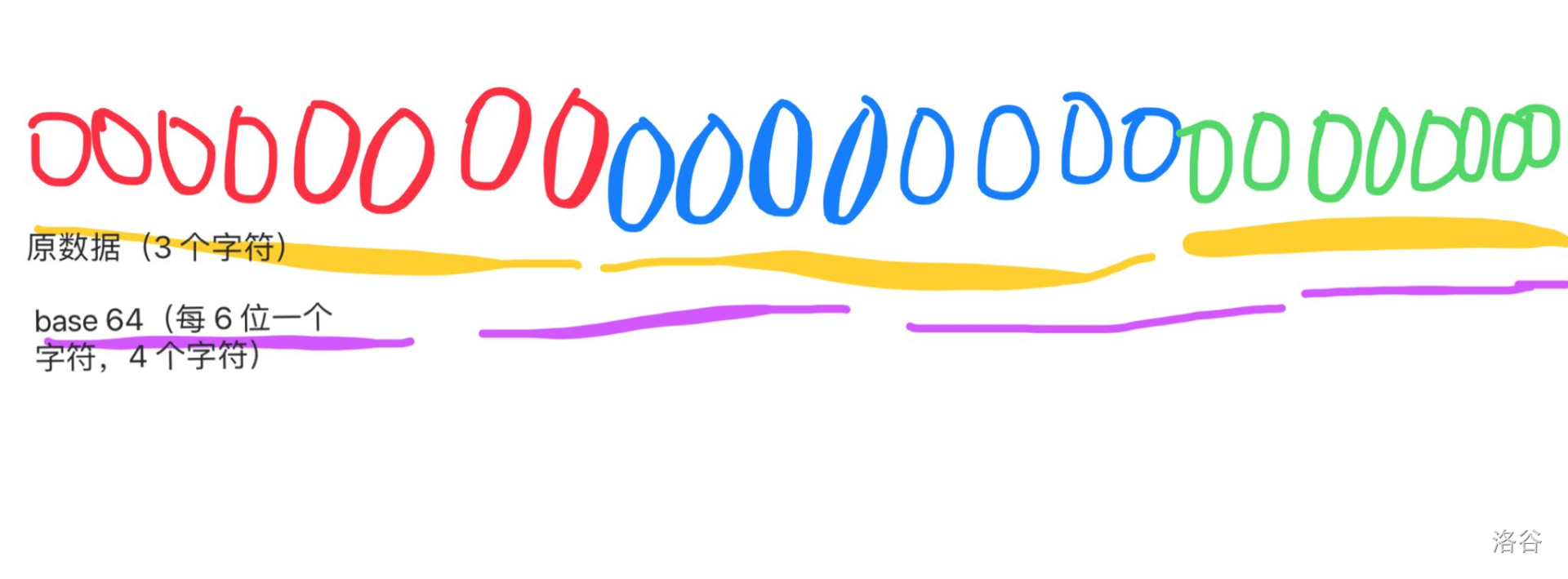
  1. 考场写的 T，考后发现解密后的内容可能有 \n 所以 F。
  2. T，base 64 不会出错的。
  3. 考场看见前面都是 T 就写了 F，stO lzj 他手算 base 64 发现应该是 Helloworld，所以 F。
  4. 肯定是线性的啊（？），B。
  5. 考场没发现是 char，选了 B。考后才知道：

char - 能在目标系统上最有效地处理的字符表示的类型（拥有与 signed char 或 unsigned char 之一相同的表示和对齐，但始终是独立的类型）。多字节字符串用此类型表示编码单元。char 的符号性取决于编译器和目标平台： ARM 和 PowerPC 的默认设置常为无符号，而 x86 与 x64 的默认设置常为有符号。

人话：不同平台输出不同，是实现定义行为，可以是 255 也可以是 -1。不知道有 int(char(0xff)) 个母亲的 CCF 会怎么改了，哈哈哈。

  1. 谁 tm 去算这玩意，没算，但注意到 A/C 少一个等号，所以 B/D 里面选就行了，蒙的 B。

做到这里，人已经写傻了。

完善 T1

怎么一股 bfs 套 dp 的味道（？）考后发现是 Dijkstra。

34 题，这不很明显的初始化，D。
35 题，考的时候以为第一次更新最优，选了 D，考后发现这是 Dijkstra 啊……第一次更新不一定最优，应该是 A……
36 题，显然是没有被访问过的最优的点（这里看得出是 Dijkstra 了其实），D。
37 题，显然要另一个访问过的点一起来更新，C。

完善 T2

传说中的四毛子算法……其实这玩意我之前看到过，但没看懂……

前三空貌似是单调栈，然而我没学过，这三个空还是比较好蒙的，反正我全蒙对了。

后三空，不会，爆零。

中午

把答案记在了准考证上，啸着爬出考场。本来想找 lzj 对答案的，结果他没记下来。

总结一下，这个 S 组好多不会，和去年考 J 组体验完全一致（去年 J 我没过初赛）。

中午膜拜了校内一群大佬，顺便对了一下民间答案，好像还挺高的（？）

J 组

官方答案：

DBACDDCABBBACBB
FFFTFB
FTTBBC
TFFACC
DCCDBBDCBD

走进 J 组考场，怎么是同一个考场同一个老师啊。

发试卷了，随便看了一下，就这？就这？就这？怎么还和上午重题呢？

2:30 开考。

选择题

  1. C 语言是面向过程的，D。
  2. 显然图灵奖啊，B。
  3. 显然 A 啊。
  4. 第一个数不用比，C。
  5. 手动模拟，D。
  6. \(m\) 条边要变成 \(n-1\)，\(m-(n-1)=m-n+1\)，D。
  7. \(2^2+2^0+2^{-1}+2^{-2}=5.75\)，C。
  8. 注意是完全二叉树，第五层最多有 \(2^{5-1}=16\) 个结点，形态数就是这 \(16\) 个结点中去掉 \(0\) 个、\(1\) 个……\(15\) 个，一共 \(16\) 种，A。
  9. 把 ABCD 全按后缀表达式的规则算一遍，B。为什么不是 C 呢？难道你的乘法是右结合的吗？
  10. \(\frac{C_6^2 C_4^2 C_2^2}{A_3^3}=15\)，除以 \(A_3^3\) 是因为不区分队伍的编号，B。
  11. 哈夫曼树是贪心，B。就这么说吧，P1090 合并果子 是贪心吧，它本质上是建一棵哈夫曼树。
  12. 枚举，没有重复数字的有 \(A_3^3=6\) 个，有 11 的有 \(2\times 3=6\)（剩下两个挑一个，插入位置有三种），22 同理，一共 \(18\) 种，A。
  13. 列表法，C。
  14. B/E 可能是最后一个遍历到的点，B。
  15. 小学数学，我竟然不会，不讲了 补题解。

果然是 J 组，和 S 组不是一个等级的，讲解字数差距真大……

阅读 T1

\(f(x)=\texttt{popcount}(x),g(x)=\texttt{lowbit}(|x|)\)。

  1. 会越界的，数组只有 \(10^3\)，F。
  2. 这种题不会没关系，你看下面不就输入了个 -65536 吗，F。
  3. \(f(10)=2,g(10)=2\)，然而它输出 \(5\)，F。
  4. 使用短除法对 \(511998\) 进行 拆分 进制转换，发现 \(511998=(111\ 1100\ 1111\ 1111\ 1110)_2\)，那么 \(f(511998)=16,g(511998)=2\)，T。
  5. 这还用说，F。
  6. 众所周知 \(2147483647=2^{31}-1\)，那口算可得 \(f(2^{31}-1)=31\)（退位退成 \(31\) 个 \(1\)），\(g(2^{31}-1)=1\)，相加得 \(32\)，直接选 B，\(-65536\) 不用看了。

阅读 T2

看到题狂笑了起来，哈哈哈这不就是上午考过的吗，太好了。

就是 base 64 解码。

  1. 反了，编码才是这个，F。话说我考时看错题了选了 T，耻辱啊（
  2. 解密后的东西可能有换行，T。没想到这一点，耻辱 * 2（
  3. 上午选择下午判断？果断 T。
  4. 简单的一重循环，为什么不是线性的？B。
  5. 这需要口算了，过程，B。
  6. 和上面一样，你需要毅力，，，C。

阅读 T3

线性筛嘿嘿嘿，，，

设 \(n=10\)，模拟一下程序运行，得到这样的表：

\(i\) \(1\) \(2\) \(3\) \(4\) \(5\) \(6\) \(7\) \(8\) \(9\) \(10\)
\(c_i\) \(0\) \(1\) \(1\) \(2\) \(1\) \(1\) \(1\) \(3\) \(2\) \(1\)
\(f_i\) \(1\) \(2\) \(2\) \(3\) \(2\) \(4\) \(2\) \(4\) \(3\) \(4\)
\(d_i\) \(0\) \(1\) \(1\) \(1\) \(1\) \(4\) \(1\) \(1\) \(1\) \(6\)
\(g_i\) \(1\) \(3\) \(4\) \(7\) \(6\) \(12\) \(8\) \(15\) \(13\) \(18\)
表格 也太 挤了 吧， 不够 位置 吗？ 很难 看诶 ！差 评！

重点关注 \(f_i,g_i\)，发现 \(f_i\) 是 \(i\) 的约数个数，\(g_i\) 是 \(i\) 的约数和。这道题差不多做完了，为什么是差不多呢，因为还有个 29 题啊。

  1. 整个程序除了 13 行之外没有用到 \(f_1,g_1\) 的地方，T。
  2. 这个不会证，没构造出数据，选了 F。
  3. 约数和不单调递增，上面那个表就不是，F。
  4. 既名为线性筛那就是线性的，A。或者也可以这样，每个合数只被标记一次，是线性的。
  5. 就是问 \([1,100]\) 有多少个数是质数，这玩意我小学时（我现在初一了）算过，\(25\) 个，C。
  6. 根据约数个数定理，\(f_{10^3}=16\)，又我觉得 \(10^3\) 的约数里有个 \(10^3\)，不可能只有 \(1340\) 这么小（？）所以 C。

完善 T1

直接暴力模拟可还行，还好不是链表（？）

显然，\(f_i=0/1\) 表示 \(i\) 在/不在圈里。

  1. 只有 \(n-1\) 人需要出圈，D。
  2. 下面是出圈，那就是要满足「报到 \(1\)」这个条件，C。
  3. 有人出圈啦，c++，C。
  4. 交替报数，D。这里科普一下 p=!p、p=1-p、p^=1 其实都是同一种意思。
  5. \(i\) 自增，由于是围成圈，B。

这题选项真有趣。

完善 T2

评测地址：AtCoder ABC218 D。

输入一堆点，排序，去重，\(O(n^2)\) 枚举左上和右下，二分找有没有左下和右上，如果有就统计答案，最后输出。

  1. 考场选的 D，考后想了一下，不是只有排序用 cmp 啊，后面还有个二分啊，应该 B。
  2. 去重，如果去重后的数组没有元素/与最近放的元素不同，就放进去，那些相同的不会被放进去，D。
  3. 如果 \(+1\)，那我们有一个反例，\(a+1=b\) 且 \(b\) 是要找的，会死循环。所以 C。实测 \(+1\) 全部 TLE。stO lsy，她说因为 ABD 都 \(+1\)，所以选 C。
  4. 如果 \(p\) 在 \(a_{mid}\) 的右边，\(a\) 就右移，B。
  5. 需要避免算了 \((i,j)\) 又算 \((j,i)\) 或者 \((i,j)\) 在一条线上两种情况，D。

下午

又记了答案，这次是笑着跑出考场，自我感觉很好。

可惜拍合照的时候我跟丢了没拍到

感觉这波 3 级绿勾稳了。

估分

https://www.luogu.com.cn/blog/yukimianyan/chu-sai-zi-ce

我的估分：放剪贴板了。

初赛稳了，爬去复习 J 组+学习 S 组了，复赛见！

posted @ 2022-11-06 19:37  caijianhong  阅读(35)  评论(0)  编辑  收藏  举报