【模板】虚树 Virtual Tree

problem

一棵树，在树上拿几个点出来说它们是关键点，让你在这些关键点上做和关键点有关的树上 DP。同时多次询问限制 \(\sum k\) 的大小，\(n,m\) 都很大。不能每次都重新跑树上 DP。

这时候，对着关键点建虚树，在虚树上 DP，即可做到 \(O(k(\log n+\log k))\) 的复杂度建立，\(O(k)\) 的点数，如果 DP 复杂度与 \(k\) 有关，加起来就爆不了了。

solution

感性理解

这里给一下虚树的定义：有关键点点集 \(S\)，那么虚树的点集为 \(S\cup\{k|i,j\in S,lca(i,j)=k\}\)，就是所有 LCA 的并。

构造方法是增量构造：首先将所有点按照 dfn 序排序，然后动态的维护一条右链，大概长这样：

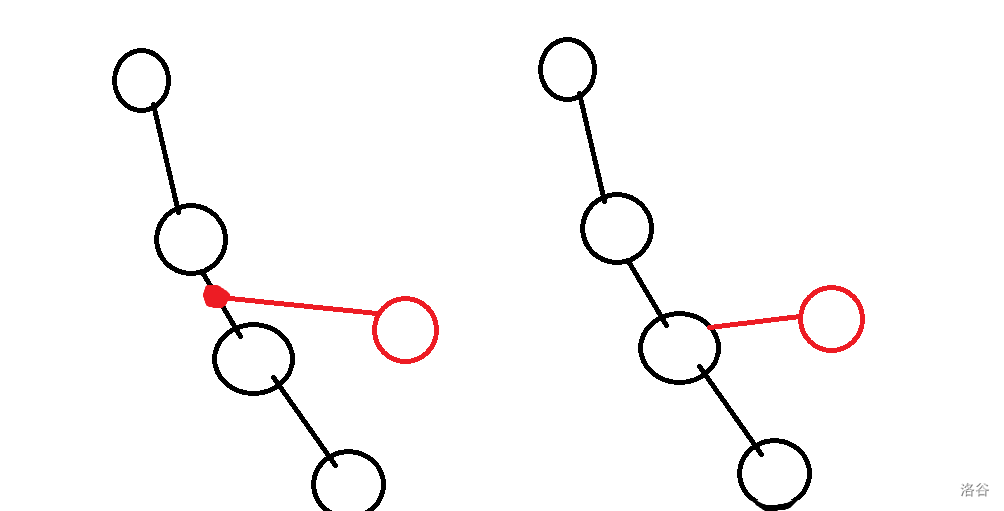
然后每次拿链底元素和当前加入的红点求个 lca 记为 \(k\)，分讨：

• \(k\) 已经在链中：将这条链截到 \(k\)，然后红点接上去。
• \(k\) 不在链中：将这条链截到 \(k\)（这条链的 dfn 序应该是单调的），然后依次接上 \(k\) 和红点。

听起来非常简单。建完虚树以后就是 DP 的事情了，虚树只是个套路。注意虚树有 \(2|S|\) 个点。

具体过程

将所有点按 dfn 序排序，维护一个单调栈 \(stk\)，记栈顶为 \(s\)，栈顶下那个点叫 \(s'\)，每次加入一个节点 \(u\)，首先求出 \(k=lca(u,s)\)，然后：

• 若 \(k=s\) 结束。
• 若 \(dfn_k<dfn_{s'}\)：连边 \(s\to s'\)，弹栈 \(s'\)，继续。
• 若 \(k=s'\)：连边 \(s\to s'\)，弹栈，结束。
• 若 \(dfn_{s'}<dfn_k\)：连边 \(s\to k\)，篡改栈顶为 \(k\)，结束。

然后将 \(u\) 入栈。最后处理完所有点后，将这条右链全部连起来

正确性

• 虚树上两个点的祖先关系仍然不变。显然了。
• 如果一个点 \(k\) 最终作为 LCA 被加入，说明在原树上它的两棵不同的子树中有关键点，将这些子树中的关键点按 dfn 序排序，相邻两个跨过两棵子树的关键点就会贡献到这个 \(k\)。
• 而观察到两个 dfn 相邻的点，只有 \(m\) 个，于是一共只有 \(m\) 个 lca，所以一共有 \(2m\) 的点加入虚树。

code

实现细节：

• 要求 LCA。树上倍增应该好写一点，因为是静态的，有的题需要查询虚树边的信息。
• 你需要一个能即时清空的图，这里给出实现方法：记录时间戳，如果这个点和当前时间不一样，清空它的 head，vector 就 clear() 一下（这里的空间显然很对，一共就 \(2m\) 条边可能加入）
• 将根节点放进去一起建虚树。

example：[SDOI2011] 消耗战

建立虚树。然后想怎么 DP 就怎么 DP。

令 \(f_u\) 表示搞定 \(u\) 子树不含 \(u\) 的最小代价。

\[f_u=\sum_v\begin{cases} w_{u\to v},&(v\text{ 是关键点}),\\ \min(w_{u\to v},f_v),&(v\text{ 不是关键点}). \end{cases}\]

[SDOI2011] 消耗战 代码实现

#include <algorithm>
#include <cstdio>
#include <cstring>
#include <utility>
#include <vector>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define debug(...) void(0)
#endif
typedef long long LL;
template <int N, int M, class T = int>
struct graph {
  int head[N + 10], nxt[M * 2 + 10], cnt;
  int vis[N + 10], tag;
  struct edge {
    int u, v;
    T w;
    edge(int u = 0, int v = 0, T w = 0) : u(u), v(v), w(w) {}
  } e[M * 2 + 10];
  graph() {
    memset(head, cnt = 0, sizeof head);
    memset(vis, tag = 0, sizeof vis);
  }
  edge& operator[](int i) { return e[i]; }
  void add(int u, int v, T w = 0) {
    if (vis[u] != tag) vis[u] = tag, head[u] = 0;
    e[++cnt] = edge(u, v, w), nxt[cnt] = head[u], head[u] = cnt;
  }
  void link(int u, int v, T w = 0) { add(u, v, w), add(v, u, w); }
};
int n, fa[19][1 << 18], mink[19][1 << 18], dep[1 << 18], dfn[1 << 18], cnt;
graph<1 << 18, 1 << 18, int> g, t;
void dfs(int u, int f = 0) {
  dep[u] = dep[fa[0][u] = f] + 1, dfn[u] = ++cnt;
  for (int i = g.head[u]; i; i = g.nxt[i])
    if (g[i].v != f) dfs(g[i].v, u), mink[0][g[i].v] = g[i].w;
}
int jump(int u, int k) {
  for (int j = 18; j >= 0; j--)
    if (k >> j & 1) u = fa[j][u];
  return u;
}
int query(int u, int k) {
  int r = 1e9;
  for (int j = 18; j >= 0; j--)
    if (k >> j & 1) r = min(r, mink[j][u]), u = fa[j][u];
  return r;
}
int lca(int u, int v) {
  if (dep[u] < dep[v]) swap(u, v);
  if (u = jump(u, dep[u] - dep[v]), u == v) return u;
  for (int j = 18; j >= 0; j--)
    if (fa[j][u] != fa[j][v]) u = fa[j][u], v = fa[j][v];
  return fa[0][u];
}
int h[1 << 18], stk[1 << 18], vis[1 << 18];
void build(int h[], int m) {
  t.tag++, t.cnt = 0, h[++m] = 1;
  //	memset(t.head,0,sizeof t.head);
  sort(h + 1, h + m + 1, [&](int i, int j) { return dfn[i] < dfn[j]; });
  int top = 1;
  stk[1] = 1;
  auto link = [&](int u, int v) {
    debug("link(%d->%d)(%d)\n", u, v, query(u, dep[u] - dep[v]));
    t.link(u, v, query(u, dep[u] - dep[v]));
  };
  for (int i = 2; i <= m; i++) {
    int k = lca(h[i], stk[top]);
    vis[h[i]] = t.tag;
    if (k != stk[top]) {
      while (top >= 2 && dfn[stk[top - 1]] > dfn[k])
        link(stk[top], stk[top - 1]), top--;
      if (stk[top - 1] == k)
        link(stk[top], k), top--;
      else
        link(stk[top], k), stk[top] = k;
    }
    stk[++top] = h[i];
  }
  while (top >= 2) link(stk[top], stk[top - 1]), top--;
}
LL solve(int u, int f = 0) {
  LL ans = 0;
  for (int i = t.head[u]; i; i = t.nxt[i]) {
    int v = t[i].v;
    if (v == f) continue;
    LL res = solve(v, u);
    if (vis[v] == t.tag)
      ans += t[i].w;
    else
      ans += min(res, (LL)t[i].w);
  }
  debug("solve(%d)=%lld\n", u, ans);
  return ans;
}
int main() {
  //	#ifdef LOCAL
  //	 	freopen("input.in","r",stdin);
  //	#endif
  scanf("%d", &n);
  for (int i = 1, u, v, w; i < n; i++)
    scanf("%d%d%d", &u, &v, &w), g.link(u, v, w);
  mink[0][1] = 1e9, dfs(1);
  for (int j = 1; j <= 18; j++) {
    for (int i = 1; i <= n; i++) fa[j][i] = fa[j - 1][fa[j - 1][i]];
    for (int i = 1; i <= n; i++)
      mink[j][i] = min(mink[j - 1][i], mink[j - 1][fa[j - 1][i]]);
  }
  scanf("%*d");
  for (int cnt; ~scanf("%d", &cnt);) {
    for (int i = 1; i <= cnt; i++) scanf("%d", &h[i]);
    build(h, cnt);
    printf("%lld\n", solve(1));
  }
  return 0;
}

另外一个模板

void buildVTree(vector<int> h) {
  static int vis[1 << 18], tim = 0, stk[1 << 18];
  if (h.empty()) return;
  ++tim;
  sort(h.begin(), h.end(), [&](int u, int v) { return dfn[u] < dfn[v]; });
  bool flag = 0;
  if (h[0] != 1)
    h.insert(h.begin(), 1);
  else
    flag = 1;
  h.erase(unique(h.begin(), h.end()), h.end());
  auto link = [&](int u, int v) {
    if (vis[u] < tim) vis[u] = tim, t[u].clear();
    if (vis[v] < tim) vis[v] = tim, t[v].clear();
    t[u].emplace_back(v, getDist(u, v));
    t[v].emplace_back(u, getDist(u, v));
  };
  int top = 0;
  stk[++top] = h[0];
  for (int i = 1; i < h.size(); i++) {
    int k = getLca(stk[top], h[i]);
    if (k != stk[top]) {
      while (top >= 2 && dfn[stk[top - 1]] > dfn[k])
        link(stk[top - 1], stk[top]), --top;
      if (stk[top - 1] == k)
        link(stk[top], k), --top;
      else
        link(stk[top], k), stk[top] = k;
    }
    stk[++top] = h[i];
  }
  while (top >= 3) link(stk[top - 1], stk[top]), --top;
  if (top >= 2 && (flag || vis[1] == tim)) link(stk[top - 1], stk[top]);
}