【模板】图论:图的连通性相关(tarjan 全家桶)
【模板】图论:图的连通性相关(tarjan 全家桶)
posted on 2022-07-07 20:52:49 | under 模板 | source
有向图缩点 / 强连通分量(SCC)
strongly connected component
现有一有向图 \(G=(V,E)\),称一个点集 \(E'\in E\) 为强连通分量,当且仅当 \(E'\) 的任意两点可以互相到达(围成一个环),求出所有极大强连通分量即 \(\tt SCC\)。
使用 Tarjan,我们将这个有向图看成一棵树,dfs 遍历,用 \(dfn_u\) 记录访问点 \(u\) 的时间戳。由于它是一个图,所以会有一些边返回到其它访问过的点(一定是祖先,这是 dfs 生成树的性质),称作返祖边。
记录 \(low_u\),它表示点 \(u\) 通过 dfs 树和最多一次返祖边能到达的最小的 \(dfn\)。如果 \(low_u=dfn_u\),我们断言点 \(u\) 的整一棵子树是一个 \(SCC\),因为从点 \(u\) 出发能回到点 \(u\),就是一个环。但是,\(low_u\) 不能经过已经缩完点的点,这样两个 \(SCC\) 就套在一起了,可以合成一个大的 \(SCC\) 了。
点击查看代码
int dfn[1010],low[1010],stk[1010],col[1010],cnt,top,tot;
void reset(){
cnt=0;
tot=0;
memset(dfn,0,sizeof dfn);
memset(col,0,sizeof col);
}
void tarjan(int u){
low[stk[++top]=u]=dfn[u]=++cnt;
for(int i=g.head[u];i;i=g.nxt[i]){
int v=g[i].v;
if(!dfn[v]) tarjan(v),low[u]=min(low[u],low[v]);
else if(!col[v]) low[u]=min(low[u],dfn[v]);
}
if(low[u]==dfn[u]){
col[u]=++tot;
while(stk[top]!=u) col[stk[top--]]=tot;
top--;
//do col[stk[top]]=css; while(stk[top--]!=u);
}
}
边双连通分量(ECC)
2-edge-connected component
边双的定义:两个点 \(u, v\) 在无向图上连通,若删去图中的任意一条边,都不能使他们不连通,则说 \(u, v\) 边双连通。边双联通具有传递性。
在缩点的基础上,强制不让它走到父亲边即可。
\(dfn_u=low_u\)。
我不知道为什么正经的做法都说是 \(low_v>dfn_u\)。但是这个代码真的能过。
点击查看代码
graph<500010,2000010> g;
int dfn[500010],low[500010],stk[500010],cnt,top,col[500010],dcc,siz[500010];
bool vis[2000010<<1];
void tarjan(int u){
dfn[u]=low[stk[++top]=u]=++cnt;
for(int i=g.head[u];i;i=g.nxt[i]){
if(vis[i]||vis[i^1]) continue;
int v=g[i].v;
if(!dfn[v]) vis[i]=vis[i^1]=1,tarjan(v),low[u]=min(low[u],low[v]);
else low[u]=min(low[u],dfn[v]);
}
if(dfn[u]==low[u]){
col[u]=++dcc;
do col[stk[top]]=dcc; while(stk[top--]!=u);
}
}
点双连通分量(BCC)
biconnected component
点双的定义:两个点 \(u, v\) 在无向图上连通,若删去图中的任意一个不是 \(u, v\) 的点,都不能使他们不连通,则说 \(u, v\) 点双连通。点双联通不一定有传递性。
无向图割点的条件为:\(low_v\geq dfn_u\),这样 \(v\) 这个儿子就走不到 \(u\),割掉 \(u\),\(v\) 就过不来了。
点双和割点一样的。但是为了求出点双连通分量需要开一个栈,还要注意一个点可能在多个点双内。
\(low_v\geq dfn_u\)。
点击查看代码
graph<500010,2000010> g,t;
int dfn[500010],low[500010],stk[500010],cnt,top;
int dcc,cut[500010],siz[500010];
void tarjan(int u){
dfn[u]=low[stk[++top]=u]=++cnt,cut[u]=1;
for(int i=g.head[u];i;i=g.nxt[i]){
int v=g[i].v;
if(!dfn[v]){
tarjan(v),low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]){
cut[u]++,dcc++;
do t.add(dcc,stk[top]); while(stk[top--]!=v);
t.add(dcc,u);
}
}else low[u]=min(low[u],dfn[v]);
}
if(!g.head[u]) t.add(++dcc,u);
}
补充:无向图割点
与点双联通分量没有区别。
点击查看代码
int dfn[500010],low[500010],stk[500010],cnt,top,cut[500010];
void tarjan(int u){
dfn[u]=low[stk[++top]=u]=++cnt,cut[u]=1;
for(int i=g.head[u];i;i=g.nxt[i]){
int v=g[i].v;
if(!dfn[v]){
tarjan(v),low[u]=min(low[u],low[v]);
if(low[v]>=dfn[u]) cut[u]++;
}else low[u]=min(low[u],dfn[v]);
}
}
for(int i=1;i<=n;i++) if(!dfn[i]) tarjan(i),cut[i]--;
int ans=0;
for(int i=1;i<=n;i++) ans+=cut[i]>=2;
//cut[i] 表示割掉 i 点会剩下多少个连通块,割点就是 cut[i]>=2
补充:instack 问题
scc 中访问到 dfs 过的点时必须需要判断是否在栈内,在栈中时才更新 low。点双、边双好像没有这个要求,不过判了更好。
补充:无向图 dfs 树上没有横叉边
你想象一下就知道了。
仙人掌与圆方树
定义
我们遇到了一类毒瘤:仙人掌。仙人掌的每条边 / 点只会在一个环上,这就是边 / 点仙人掌。值得注意的是 \(m\leq 2n\)。
我们还是去找环,或者叫点双连通分量。在每个环中间建一个方点,连向环上其他的点(原图的点称作圆点),然后将这个环删了。这就是圆方树。
解释为什么是点双。这里是一个定义问题,两个边双可以合成一个大边双。如果是边仙人掌则一定是说点双,如果是点仙人掌(点仙人掌都是边仙人掌)则说是点双边双都可以。
注意:为了方便处理,一般一条边也算作一个点双,要在中间插一个方点。
结论:只有圆方边的圆方树上,非叶子节点一定是原图的割点。
来自洛谷题解区的图:source
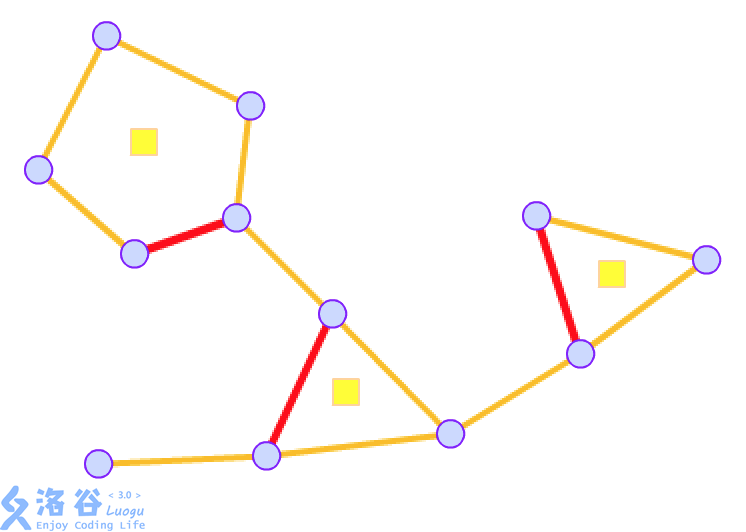
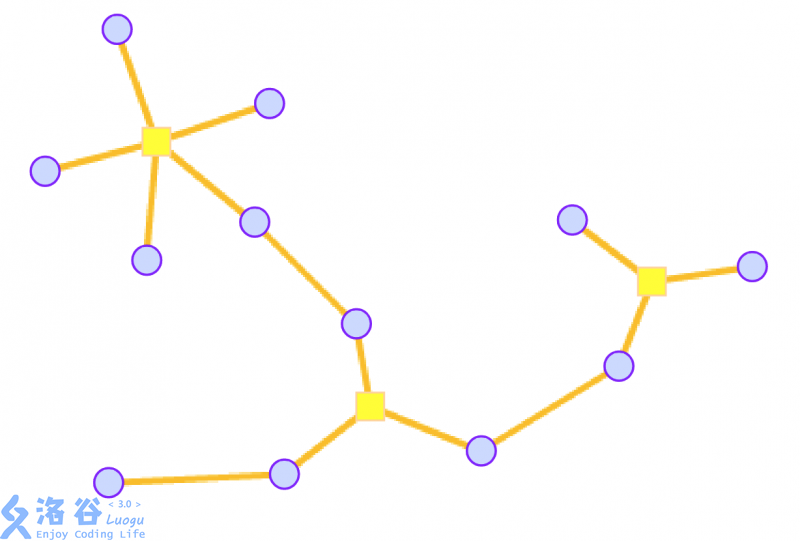
过程
找环
你还是 tarjan,求出 \(dfn,low\),最后遍历 \(u\) 的所有儿子 \(v\),如果满足:\(v\) 的上一个节点不是 \(u\),\(dfn_v>dfn_u\),就说明这是一个从 \(u\) 出发的环的末尾。我们从这里开始,跳这些点(在搜索树上的)前驱,直到 \(u\),就能把环找出来。
边权
假设是仙人掌上最短路。对于圆圆边,保留原边权(但其实我们并不推荐写圆圆边)。对于方方边,好像没有这样的边。是的。
对于圆方边,假如这个环离根最近的节点(或者说进入环的节点)是 \(u\),方点是 \(k\),那么 \((k,u)\) 的边权是 \(0\)(或者叫加法单位元?),\((k,v)\) 的边权,就是 \(v\to u\) 在环上的距离。这样的正确性在于,跳到方点相当于跳到 \(u\) 上。
如何求环上两点间最短距离?做出前缀和 \(sum_i\),那么两点之间最短路是
自己 swap 一下 \(u, v\) 的顺序。
答案
圆方树是树,可以求 LCA,记 \(u,v\) 的 LCA 为 \(k\)。
- 若 \(k\) 是圆点,直接树上前缀和。
- 若 \(k\) 是方点,假设它们跳的前一步(在环上的)的点是 \(u',v'\),答案是 \(u\to u'\) 加上 \(v\to v'\) 加上 \(u'\to v'\) 的最短路。
代码
洛谷 P5236 【模板】静态仙人掌
(注意这个写的是有圆圆边的广义圆方树)
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define debug(...) void(0)
#endif
typedef long long LL;
template <int N, int M, class T = int>
struct graph {
int head[N + 10], nxt[M * 2 + 10], cnt, tot;
struct edge {
int u, v;
T w;
edge(int u = 0, int v = 0, T w = 0) : u(u), v(v), w(w) {}
} e[M * 2 + 10];
edge& operator[](int i) { return e[i]; }
graph() { memset(head, cnt = 0, sizeof head); }
void add(int u, int v, T w = 0) {
e[++cnt] = edge(u, v, w), nxt[cnt] = head[u], head[u] = cnt;
}
void link(int u, int v, T w = 0) { add(u, v, w), add(v, u, w); }
};
int n, m, sum[100010], fa[18][100010], up[100010], dep[100010];
graph<100010, 200010> g, t;
int getdist_cycle(int u, int v, int k) {
if (sum[u] < sum[v]) swap(u, v);
return min(sum[u] - sum[v], sum[k] - sum[u] + sum[v]);
}
void make_cycle(int u, int v, int val) {
sum[v] = val;
for (int i = v; i != u; i = fa[0][i]) sum[fa[0][i]] = sum[i] + up[i];
sum[++t.tot] = sum[u], sum[u] = 0;
t.link(t.tot, u, 0);
for (int i = v; i != u; i = fa[0][i])
t.link(t.tot, i, getdist_cycle(i, u, t.tot));
}
int dfn[100010], low[100010], cnt;
void tarjan(int u, int f = 0) {
dfn[u] = low[u] = ++cnt, fa[0][u] = f;
for (int i = g.head[u]; i; i = g.nxt[i]) {
int v = g[i].v;
if (!dfn[v])
up[v] = g[i].w, tarjan(v, u), low[u] = min(low[u], low[v]);
else if (v != f)
low[u] = min(low[u], dfn[v]);
if (low[v] > dfn[u]) t.link(u, v, g[i].w);
}
for (int i = g.head[u]; i; i = g.nxt[i]) {
int v = g[i].v;
if (fa[0][v] != u && dfn[v] > dfn[u]) make_cycle(u, v, g[i].w);
}
}
void dfs(int u, int f = 0) {
dep[u] = dep[fa[0][u] = f] + 1;
for (int i = t.head[u]; i; i = t.nxt[i])
if (t[i].v != f) up[t[i].v] = up[u] + t[i].w, dfs(t[i].v, u);
}
int jump(int u, int k) {
for (int j = 17; j >= 0; j--)
if (k >> j & 1) u = fa[j][u];
return u;
}
int lca(int u, int v) {
dep[u] < dep[v] ? v = jump(v, dep[v] - dep[u]) : u = jump(u, dep[u] - dep[v]);
for (int j = 17; j >= 0; j--)
if (fa[j][u] != fa[j][v]) u = fa[j][u], v = fa[j][v];
return u == v ? u : fa[0][u];
}
int main() {
scanf("%d%d%*d", &n, &m);
for (int i = 1, u, v, w; i <= m; i++)
scanf("%d%d%d", &u, &v, &w), g.link(u, v, w);
t.tot = n, tarjan(1), dfs(1);
debug("graph t:\n");
for (int i = 1; i <= t.cnt; i += 2)
debug("(%d, %d) = %d\n", t[i].u, t[i].v, t[i].w);
for (int i = 1; i <= t.tot; i++) debug("sum[%d] = %d\n", i, sum[i]);
for (int i = 1; i <= t.tot; i++) debug("up[%d] = %d\n", i, up[i]);
for (int j = 1; j <= 17; j++)
for (int i = 1; i <= t.tot; i++) fa[j][i] = fa[j - 1][fa[j - 1][i]];
for (int u, v; ~scanf("%d%d", &u, &v);) {
int k = lca(u, v);
if (k <= n)
printf("%d\n", up[u] + up[v] - 2 * up[k]);
else {
int ub = jump(u, dep[u] - dep[k] - 1), vb = jump(v, dep[v] - dep[k] - 1);
printf("%d\n",
up[u] - up[ub] + up[v] - up[vb] + getdist_cycle(ub, vb, k));
}
}
return 0;
}
洛谷 P10203 [湖北省选模拟 2024] 玩具销售员 / tartaglia
(这个是圆方树 dp,更具有代表性)
#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define endl "\n"
#define debug(...) void(0)
#endif
typedef long long LL;
template <class T>
using must_int = enable_if_t<is_integral<T>::value>*;
template <unsigned umod>
struct modint {
static constexpr int mod = umod;
unsigned v;
modint() : v(0) {}
template <class T, must_int<T> = nullptr>
modint(T x) {
x %= mod, v = x < 0 ? x + mod : x;
}
friend int raw(modint self) { return self.v; }
friend ostream& operator<<(ostream& os, modint self) {
return os << raw(self);
}
modint& operator+=(const modint& rhs) {
v += rhs.v;
if (v >= umod) v -= umod;
return *this;
}
modint& operator-=(const modint& rhs) {
v -= rhs.v;
if (v >= umod) v += umod;
return *this;
}
modint& operator*=(const modint& rhs) {
v = 1ull * v * rhs.v % umod;
return *this;
}
modint& operator/=(const modint& rhs) {
assert(rhs.v);
return *this *= qpow(rhs, mod - 2);
}
template <class T, must_int<T> = nullptr>
friend modint qpow(modint a, T b) {
modint r = 1;
for (; b; b >>= 1, a *= a)
if (b & 1) r *= a;
return r;
}
friend modint operator+(modint lhs, const modint& rhs) { return lhs += rhs; }
friend modint operator-(modint lhs, const modint& rhs) { return lhs -= rhs; }
friend modint operator*(modint lhs, const modint& rhs) { return lhs *= rhs; }
friend modint operator/(modint lhs, const modint& rhs) { return lhs /= rhs; }
};
typedef modint<998244353> mint;
template <int N, int M, class T>
struct graph {
int head[N + 10], nxt[M << 1], cnt;
struct edge {
int u, v;
T w;
};
edge e[M << 1];
edge& operator[](int i) { return e[i]; }
graph() { memset(head, 0, sizeof head), cnt = 1; }
void add(int u, int v, T w) {
e[++cnt] = {u, v, w}, nxt[cnt] = head[u], head[u] = cnt;
}
void link(int u, int v, T w) { add(u, v, w), add(v, u, w); }
};
int n, m, Q;
graph<300010, 300010, mint> g;
namespace subtaskA {
mint f[300010];
void dfs(int u, int fa) {
f[u] = 1;
for (int i = g.head[u]; i; i = g.nxt[i]) {
int v = g[i].v;
if (v == fa) continue;
dfs(v, u);
f[u] += f[v] * g[i].w;
}
}
void dp(int u, int fa) {
for (int i = g.head[u]; i; i = g.nxt[i]) {
int v = g[i].v;
if (v == fa) continue;
mint ofv = f[v];
f[v] += (f[u] - f[v] * g[i].w) * g[i].w;
dp(v, u);
}
}
mint* solve() { return dfs(1, 0), dp(1, 0), f; }
}; // namespace subtaskA
namespace subtaskC { // "C" stands for "cactus"!
int cid[300010];
struct cycle {
int len;
vector<int> dts;
vector<mint> pre, pri;
cycle() : pre({1}) {}
void add(int u, mint w) {
cid[u] = dts.size();
dts.push_back(u);
pre.push_back(w);
}
void build() {
len = pre.size() - 1;
pri.resize(len + 1);
pri[len] = 1;
for (int i = 1; i <= len; i++) pri[len] *= pre[i];
pri[len] = 1 / pri[len];
for (int i = len; i >= 1; i--) pri[i - 1] = pri[i] * pre[i];
for (int i = 1; i <= len; i++) pre[i] *= pre[i - 1];
}
mint query(int u, int v) {
u = cid[u], v = cid[v];
if (u > v) swap(u, v);
mint w1 = pre[v] * pri[u];
mint w2 = pre[len] * pri[v] * pre[u];
return w1 + w2 - w1 * w2;
}
};
graph<600010, 600010, mint> t;
int dfn[300010], tot;
cycle cyc[600010];
void tarjan(int u) {
static int low[300010], stk[300010], cnt, top;
static bool vie[300010 << 1];
static mint tmp[300010], pre[300010];
dfn[u] = low[u] = ++cnt;
stk[++top] = u;
for (int i = g.head[u]; i; i = g.nxt[i]) {
if (vie[i] || vie[i xor 1]) continue;
vie[i] = vie[i xor 1] = true;
int v = g[i].v;
if (!dfn[v]) {
pre[v] = g[i].w;
tarjan(v);
low[u] = min(low[u], low[v]);
if (low[v] > dfn[u]) {
t.link(u, v, g[i].w);
assert(stk[top] == v);
--top;
} else if (low[v] == dfn[u]) {
int p = ++tot;
debug("new cycle: %d, ", u);
t.link(p, u, 0);
cyc[p].add(u, tmp[u]);
do {
t.link(p, stk[top], 0);
cyc[p].add(stk[top], pre[stk[top]]);
debug("%d, ", stk[top]);
} while (stk[top--] != v);
debug("\n");
cyc[p].build();
}
} else {
if (dfn[v] < low[u]) tmp[v] = g[i].w;
low[u] = min(low[u], dfn[v]);
}
}
}
mint h[300010], f[300010];
void dfs(int u, int fa) {
f[u] = 1;
for (int i = t.head[u]; i; i = t.nxt[i]) {
int v = t[i].v;
if (v == fa) continue;
if (v <= n) {
dfs(v, u);
f[u] += f[v] * t[i].w;
} else {
for (int z : cyc[v].dts) {
if (z == u) continue;
dfs(z, v);
f[u] += f[z] * cyc[v].query(u, z);
}
}
}
debug("f[%d] = %d\n", u, f[u]);
}
void dp(int u, int fa) {
h[u] = f[u];
for (int i = t.head[u]; i; i = t.nxt[i]) {
int v = t[i].v;
if (v == fa) continue;
if (v <= n) {
f[v] += (f[u] - f[v] * t[i].w) * t[i].w;
dp(v, u);
} else {
for (int z : cyc[v].dts) {
if (z == u) continue;
f[u] -= f[z] * cyc[v].query(u, z);
}
assert(cyc[v].dts.front() == u);
int sz = cyc[v].dts.size();
mint prd = cyc[v].pre[cyc[v].len];
vector<mint> w1s(sz + 1, 0), w2s(sz + 1, 0), w3s(sz + 1, 0);
for (int i = sz - 1; i >= 1; i--) {
int z = cyc[v].dts[i];
w1s[i] = w1s[i + 1] + f[z] * cyc[v].pre[i];
w2s[i] = w2s[i + 1] + f[z] * cyc[v].pri[i] * prd;
w3s[i] = w3s[i + 1] + f[z];
}
mint w1p = f[u] * cyc[v].pri[0], w2p = f[u] * cyc[v].pre[0] * prd,
w3p = f[u];
for (int i = 1; i < sz; i++) {
int z = cyc[v].dts[i];
mint ofz = f[z];
f[z] += (w1p + w2s[i + 1]) * cyc[v].pre[i];
f[z] += (w2p + w1s[i + 1]) * cyc[v].pri[i];
f[z] -= (w3p + w3s[i + 1]) * prd;
dp(z, v);
w1p += ofz * cyc[v].pri[i];
w2p += ofz * cyc[v].pre[i] * prd;
w3p += ofz;
}
}
}
}
mint* solve() {
tot = n;
tarjan(1);
for (int i = 1; i <= n; i++) assert(dfn[i]);
dfs(1, 0);
dp(1, 0);
return h;
}
}; // namespace subtaskC
int main() {
#ifndef LOCAL
cin.tie(nullptr)->sync_with_stdio(false);
#endif
cin >> n >> m >> Q;
for (int i = 1; i <= m; i++) {
int u, v, p, q;
cin >> u >> v >> p >> q;
g.link(u, v, mint(p) / q);
}
mint* fans;
if (n == m + 1)
fans = subtaskA::solve();
else
fans = subtaskC::solve();
while (Q--) {
int x;
cin >> x;
cout << fans[x] << endl;
}
return 0;
}
crxis 缩点
由 crxis 提出的缩点算法。我认为没有比 tarjan 好到哪里去,应该忽略之。
https://www.cnblogs.com/caijianhong/p/16863460.html
2-sat 问题
一句话概括,将 bool 变量的两种取值拆成两个点,然后对于一个限制:\(f_u=a\) 和 \(f_v=b\) 至少有一个成立(可以两个都成立),就是说若 \(f_u\neq a\) 那么必然 \(f_v=b\),若 \(f_v\neq b\) 那么必然 \(f_u=a\)。其他的限制都可以用这个推出了。例如钦定某命题为假,就是这个命题为假和这个命题为假至少有一个成立。
点击查看代码
template <int N>
struct two_sat {
vector<int> g[N << 1];
int cnt, top, col;
int dfn[N << 1], stk[N << 1], scc[N << 1], low[N << 1];
two_sat() {
for (int i = 0; i < N << 1; i++) g[i].clear();
}
void add_clause(int u, bool f, int v, bool h) {
//debug("add_clause(%d, %d, %d, %d)\n", u, f, v, h);
//至少有一个成立
g[u + !f * N].push_back(v + h * N);
g[v + !h * N].push_back(u + f * N);
}
void tarjan(int u) {
stk[++top] = u;
dfn[u] = low[u] = ++cnt;
for (int v: g[u]) {
if (!dfn[v]) tarjan(v), low[u] = min(low[u], low[v]);
else if (!scc[v]) low[u] = min(low[u], dfn[v]);
}
if (dfn[u] == low[u]) {
scc[u] = ++col;
do scc[stk[top]] = col;
while (stk[top--] != u);
}
}
bool satisfiable() {
memset(dfn, 0, sizeof dfn);
memset(scc, 0, sizeof scc);
cnt = top = col = 0;
for (int i = 0; i < N << 1; i++)
if (!dfn[i]) tarjan(i);
for (int i = 0; i < N; i++)
if (scc[i] == scc[i + N]) return 0;
return 1;
}
};
本文来自博客园,作者:caijianhong,转载请注明原文链接:https://www.cnblogs.com/caijianhong/p/template-tarjan.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号