【模板】后缀自动机 SAM、后缀树、广义后缀自动机

posted on 2022-08-07 20:50:14 | under 模板 | source
updated on 20230727：增补更多细节，合并广义 SAM 相关。

点击查看闲话

广义后缀自动机，建议看这篇理解会更深（口语化警告） <- 已经加入后缀自动机豪华套餐

保存：基本子串结构 https://www.cnblogs.com/crashed/p/17382894.html 2023 xtq

炫酷后缀树魔术 https://www.luogu.com.cn/blog/EternalAlexander/xuan-ku-hou-zhui-shu-mo-shu

众所周知，后缀自动机有 $114514$ 种理解方式，我也无法理解，~~但是明天模拟赛要考~~，所以要学习一下。

感谢 @sshwy 的课件。/bx

UPD：考了，不会。

后缀自动机

后缀自动机（Suffix Automaton，SAM）是一种有限状态自动机，接受字符串 $S$ 的所有后缀。若认为字符集大小为常数，则它有着 $O (n)$ 的时间复杂度和 $O (n)$ 的空间复杂度（两倍）。

概念

在后缀自动机中，每一个状态对应着 $S$ 的一类子串，它们有着相同的出现位置（右边），长度互不相同，若按长度排序，则前一个是后一个的后缀。定义 $δ (p, r)$ 为状态 $p$ 末尾加上字符 $r$ 后转移到的状态，容易发现 SAM 是一个 DAG。

Endpos 集合： $S$ 的子串 $s$ 的 Endpos 集合定义为它在 $S$ 中出现的位置的右端点。以下记为 $e n d p o s (s)$ 。显然 $| e n d p o s (s) |$ 是 $s$ 在 $S$ 中的出现次数。
等价类：一个等价类中的所有子串都有着完全一致的 $e n d p o s$ ，且它们的长度是连续的。一个状态（点）表示的正是一个等价类，并且 $S$ 的任意子串都唯一归属一个等价类。显然，两个等价类要么包含要么不交（反证法）。我们可以用 $(s, l e n)$ 表示一个最长子串是 $s$ ，最长子串长度为 $l e n$ 的一个等价类，显然它是唯一的。如果 $e n d p o s = {r}$ ，可以简单认为这个等价类的所有子串以 $r$ 为右端点，左端点在左边连续，最左的左端点对应的长度为 $l e n$ ，最右的是 $l e n_{l i n k} + 1$ （等会交 $l i n k$ 的定义）
包含类：若两个等价类 $s, s^{'}$ 满足 $e n d p o s (s) \subset e n d p o s (s^{'})$ ，则称 $s^{'}$ 是 $s$ 的包含类。（注意这里是反过来的包含）若 $s^{'}$ 是 $s$ 的包含类，那么 $s^{'}$ 的最长子串比 $s$ 的最长子串短， $e n d p o s$ 更多，出现次数更多，或者更加迫真， $s^{'}$ 全是 $s$ 的后缀。
Link 指针 / 后缀链接：所有状态都有 Link 指针（根状态没有），它们构成一棵 Link 树，在 Link 树上状态 $u$ 的所有祖先都是它的包含类， $u$ 的 Link 指针指向了 $u$ 的所有包含类中最长子串长度最大的，记为 $l i n k (u)$ 。或者更加迫真， $l i n k (u)$ 是 $u$ 砍掉一段前缀的结果。
转移指针 $δ (u, r)$ 是将 $u$ 这个等价类后面加一个字符 $r$ 形成的新的等价类。可以确定的是 $u + r \subseteq δ (u, r)$ 。（ $u + r$ 这里表示等价类所有子串全部加上 $r$ ）

构造（理解一）

现在开始构造后缀自动机，我们使用增量构造法，现在我们有了 $S$ 的 SAM，我们试图构造 $S + r$ 的 SAM。（ $r$ 是一个字符）

首先新建状态节点 $u$ 表示一个等价类 $(S + r, | S | + 1)$ 。考虑两件事情：

$l i n k (u)$ 是什么？
哪些状态会转移到 $u$ ？/ 哪些 $δ (q, r)$ 会被更新？

令 $p = (S, | S |)$ 。将 $p$ 不断地在 Link 树上跳，遇到的第一个 $δ (p^{'}, r) \neq \emptyset$ 的点记为 $p^{'}$ 。那么 $q = δ (p^{'}, r)$ 是 $u$ 的等价类。

重新看一遍 $δ$ ，可以发现 $δ (p, r)$ 还包含除了 $p + r$ 外的其他串。即 $δ (p, r)$ 是包含 $p + r$ 的串。那么我们往 SAM 里放了一个 $r$ ，对应的 $q$ 中属于 $p^{'} + r$ 的字符串的出现次数都增加一，其它的不能加。遂分类讨论：

$p^{'} + r = q$ ，整个 $q$ 都可以留着，出现次数一起加一， $l i n k (u) = q$ 。
$p^{'} + r ⊊ q$ ，那么 $q$ 中有些字符串要加一，有些不用，我们把它们 split 开，原本 $q = (s, l e n)$ 会被划分成 $q_{1} = (s, | p^{'} | + 2)$ 和 $q_{2} = (s [| s | - | p^{'} |, | s |], l e n)$ ，其中 $q_{2}$ 是 $q_{1}$ 的包含类， $l i n k (u) = q_{2}$ 。代码实现中我们可以令 $q = q_{1}$ ，新开节点 $q_{2}$ 。

那么怎么更新 $δ$ ？只跟 $q, u$ 有关的需要更新，具体地，

更新 $p$ 到 $p^{'}$ Link 树上的点 $p^{″}$ ， $δ (p^{″}, r) = u$ 。
若 $q$ 分裂了，若 $p^{″} \in [p^{'}, r o o t]$ 满足 $δ (p^{″}, r) = q$ ，则更新成 $q_{2}$ 。

~~上面的我看不懂，照抄了黄队课件，Orz~~

构造（理解二）

现在开始增量构造。假如我们有一个 $t a i l$ 表示上一次加入的那个整串。加入字符 $r$ ，新开一个 $u$ 表示新的整串。时刻记住，我们要维护出边和后缀链接。显然 $c h_{t a i l, r} = u$ ，从 $t a i l$ 往上跳 $l i n k$ 到 $p$ ，这是在砍掉前缀，如果 $c h_{p, r} = \emptyset$ 那么接上 $c h_{p, r} = u$ 。如果 $c h_{p, r} \neq \emptyset$ ，因为我们在砍前缀，再砍它的出边也存在，所以我们在这里停下来更新。令 $q = c h_{p, r}$ 。我们很天真地想要 $l i n k_{u} = q$ ，这不好。

对于一个出现位置，有颜色的部分，是可能的子串左端点。显然 $p$ 在这里面。如果 $p + r$ 刚好是 $q$ （绿色图），那么直接 $l i n k_{u} = q$ 是正确的。否则（红色图）我们就会发现，对于黑线右边的这一部分子串，它们的 $e n d p o s$ 的集合加上 $n$ ，但是左边这一部分子串不是，这两部分已经不一样了。所以我们要分裂，假设我们分裂出 $c q$ ，那么使 $c q$ 成为黑线右边这一部分， $q$ 成为黑线左边的，根据定义，此时 $l i n k_{c q}$ 为原来的 $l i n k_{q}$ ， $l i n k_{q}$ 改成 $c q$ （因为要保证 $e n d p o s$ 的大小，越往上跳越多； $q$ 的后缀确实是 $c q$ ）； $l i n k_{u} = c q$ ，就是说 $u$ 贡献的这个 $e n d p o s$ 不会给到 $q$ ，这是正确的。对于 $c q$ 的出边，和 $q$ 是一模一样的。对于 $p$ 剩下的 $l i n k$ ，如果有 $c h_{p^{'}, r} = q$ 那么改成 $c h_{p^{'}, r} = c q$ 。完成。

广义 SAM 相关

这里不对什么东西进行证明，只说正确的。广义 SAM 其实就是插入新的字符串时令 $t a i l = 1$ 重新插入即可。但这样会有问题： $c h_{t a i l, r}$ 一开始就存在怎么办？我们对此进行特判即可，直接分裂 $c h_{t a i l, r}$ ，和刚才讲的一样。然后代码中有点细节要改改，分裂的时候不一定要使得 $l i n k_{u} = c q$ （你连 $u$ 都没有）。参考的实现将 expand 和 split 分成两个函数，可参考。

code

注意双倍空间！

SAM

template<int N,int M=26> struct suffixam{
    int tot,ch[N*2+10][M],link[N*2+10],len[N*2+10],siz[N*2+10],last;
    suffixam():tot(1),last(1){memset(ch,0,sizeof ch),memset(siz,0,sizeof siz),len[1]=link[1]=0;}
    void expand(int r){
        int u=++tot,p=last;last=u;
        len[u]=len[p]+1,siz[u]=1;
        while(p&&!ch[p][r]) ch[p][r]=u,p=link[p];
        if(!p) return void(link[u]=1);
        int q=ch[p][r];
        if(len[q]==len[p]+1) return void(link[u]=q);
        int cq=++tot;memcpy(ch[cq],ch[q],sizeof ch[cq]);
        len[cq]=len[p]+1,link[cq]=link[q];
        link[u]=link[q]=cq;
        while(p&&ch[p][r]==q) ch[p][r]=cq,p=link[p];//不要写错！
    }
};

广义 SAM

template <int N, int M>
struct suffixam {
  int ch[N << 1][M], tot, link[N << 1], len[N << 1];
  suffixam() : tot(1) {
    len[1] = link[1] = 0;
    memset(ch[1], 0, sizeof ch[0]);
  }
  int split(int p, int q, int r) {
    if (len[q] == len[p] + 1) return q;
    int u = ++tot;
    len[u] = len[p] + 1;
    memcpy(ch[u], ch[q], sizeof ch[0]);
    link[u] = link[q];
    link[q] = u;
    for (; p && ch[p][r] == q; p = link[p]) ch[p][r] = u;
    return u;
  }
  int expand(int p, int r) {
    if (ch[p][r]) return split(p, ch[p][r], r);
    int u = ++tot;
    len[u] = len[p] + 1;
    memset(ch[u], 0, sizeof ch[0]);
    for (; p; p = link[p]) {
      if (ch[p][r]) {
        link[u] = split(p, ch[p][r], r);
        return u;
      } else {
        ch[p][r] = u;
      }
    }
    link[u] = 1;
    return u;
  }
};

广义 SAM 使用 `unordered_map` 存转移边（这个代码很慢，除非字符集大小不可接受否则不应选用，若字符串总长过大考虑换用 map）

template <int N>
struct suffixam {
  unordered_map<int, int> ch[N << 1];
  int tot, link[N << 1], len[N << 1];
  suffixam() : tot(1) {
    ch[1].clear();
    len[1] = link[1] = 0;
  }
  int split(int p, int q, int r) {
    if (len[q] == len[p] + 1) return q;
    int u = ++tot;
    len[u] = len[p] + 1;
    ch[u] = ch[q];
    link[u] = link[q];
    link[q] = u;
    for (; p && ch[p][r] == q; p = link[p]) ch[p][r] = u;
    return u;
  }
  int expand(int p, int r) {
    if (ch[p][r]) return split(p, ch[p][r], r);
    int u = ++tot;
    len[u] = len[p] + 1;
    ch[u].clear();
    for (; p; p = link[p]) {
      if (ch[p][r]) {
        link[u] = split(p, ch[p][r], r);
        return u;
      } else {
        ch[p][r] = u;
      }
    }
    link[u] = 1;
    return u;
  }
  template <bool rev>
  vector<int> bucketsort() {
    vector<int> per(tot), buc(tot + 1);
    for (int i = 1; i <= tot; i++) buc[len[i]] += 1;
    for (int i = 1; i <= tot; i++) buc[i] += buc[i - 1];
    for (int i = 1; i <= tot; i++) per[--buc[len[i]]] = i;
    if (rev) reverse(per.begin(), per.end());
    return per;
  }
};

最后可能需要用到得到 $e n d p o s$ 集合的大小：需要建图预处理，具体的见下一节：

点击查看代码

//method 1：暴力建图 dfs
LL dfs(int u,int fa=0){
    LL ans=0;
    for(int i=g.head[u];i;i=g.nxt[i]){
        int v=g[i].v; if(v==fa) continue;
        ans=max(ans,dfs(v,u)),t.siz[u]+=t.siz[v];
    }
    if(t.siz[u]>1) ans=max(ans,1ll*t.siz[u]*t.len[u]);
    return ans;
}
for(int i=2;i<=t.tot;i++) g.add(t.link[i],i);
//method 2：拓扑排序
int q[N*2+10],inn[N*2+10];
LL toposort(){
    int L=1,R=0;LL ans=0;
    for(int i=1;i<=tot;i++) inn[link[i]]++;
    for(int i=1;i<=tot;i++) if(!inn[i]) q[++R]=i;
    while(L<=R){
        int u=q[L++];
        siz[link[u]]+=siz[u];
        if(siz[u]>1) ans=max(ans,1ll*siz[u]*len[u]);
        if(--inn[link[u]]==0) q[++R]=link[u];
    }
    return ans;
}
//method 3：桶排序求拓扑序
int per[N*2+10],buc[N*2+10];
LL toposort(){
    memset(buc,0,sizeof buc);
    for(int i=1;i<=tot;i++) buc[len[i]]++;
    for(int i=1;i<=tot;i++) buc[i]+=buc[i-1];
    for(int i=tot;i>=1;i--) per[buc[len[i]]--]=i;
    LL ans=0;
    for(int i=tot;i>=1;i--){
        int u=per[i];
        if(siz[u]>1) ans=max(ans,1ll*siz[u]*len[u]);
        siz[link[u]]+=siz[u];
    }
    return ans;
}

要求得 $e n d p o s (u)$ 的大小或者具体值，我们需要在每次插入后在返回的 $l a s t$ 节点中打上一个标记（用一个数组或者线段树）表示这个 $l a s t$ 的 $e n d p o s (u)$ 里面有一个 [插入的第几次] 位置，且 $l a s t$ 的所有后缀链接上，由于是包含类，所以都有这个 $e n d p o s$ 。插入完了之后，每个点真实的 $e n d p o s$ 是它在 Link 树上的子树的 $e n d p o s$ 的并。（如果代码没有写错，则每个点都有不为空的 $e n d p o s$ ）在求这个真实 $e n d p o s$ 时可以考虑将所有点按照 $l e n$ 倒序排序，那么这就是 Link 根向树的拓扑序。

后缀树

我们考虑一个无脑的东西：后缀树。它把 $S$ 的的所有后缀插入到 Trie 里，并拿出结束点（下文称关键点）建虚树，空间是 $O (n)$ 的。

SAM 与后缀树的联系

我们有定理：

反串 SAM 的 Link 树是其正串的后缀树。
简单推论：反串 SAM 向下跳 $l i n k$ 等价于正串上跳 $δ$ 。

那么所有概念都清晰了：

等价类：后缀树上一个关键点和上方的非关键点。（不建虚树）
包含类：后缀树上的祖先。
$q$ 分裂的分类讨论：本质上是判断 $q$ 是否为关键点，不是就分裂。
增量构造：例如原串 bbaba，插入字符 b，实际上就是反串前面插入这个字符，即在后缀树上插入 bababb。

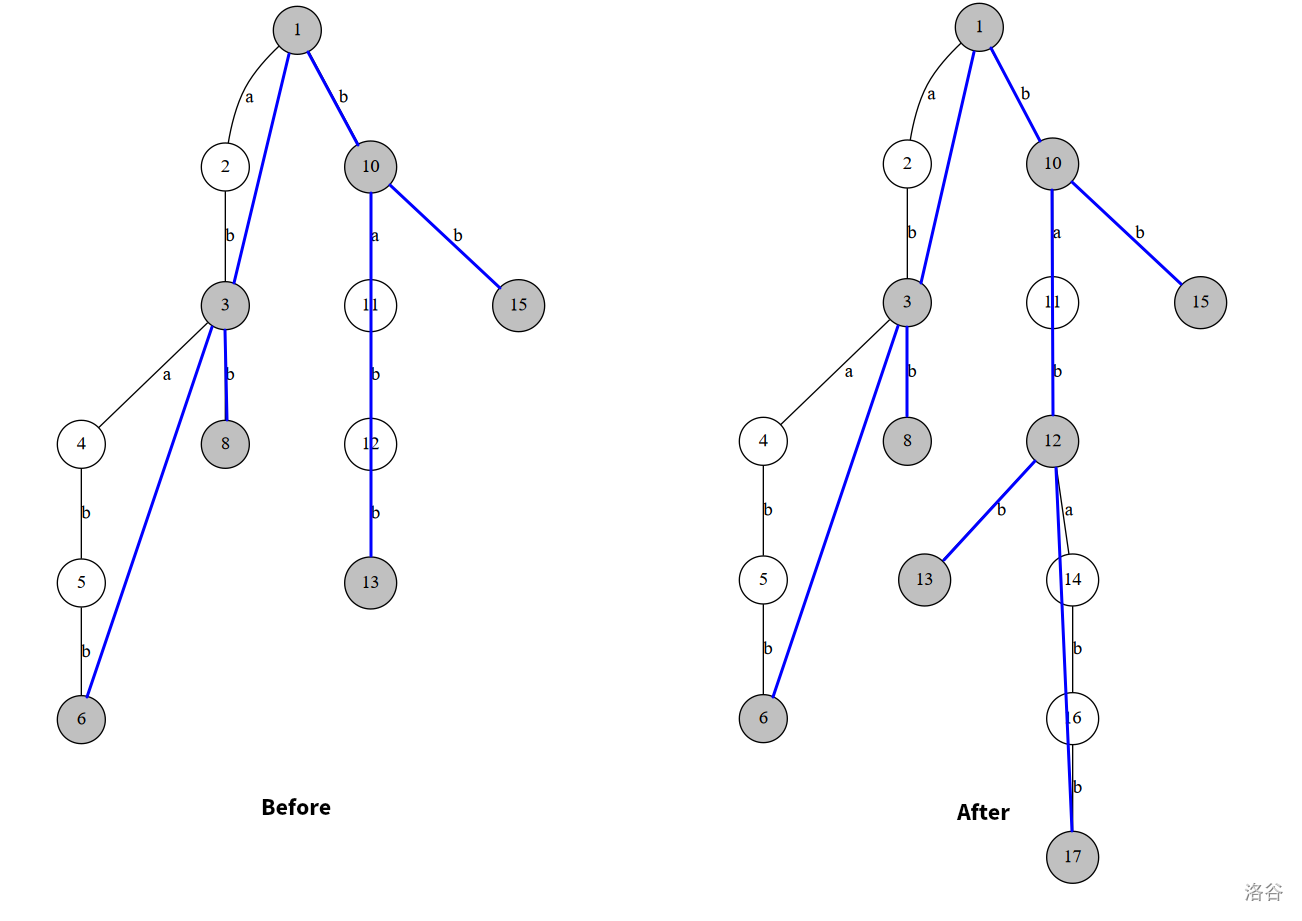
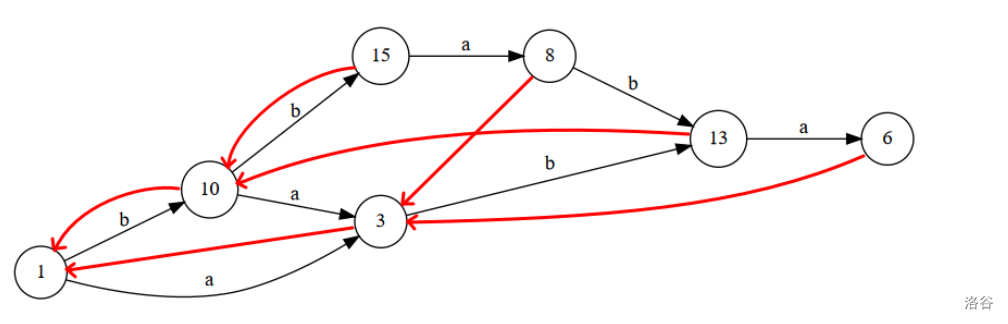
一模一样。

那么它们有什么区别？其实没有（如果不涉及什么匹配），正串 SAM 是在 Link 树上搞事情，反串 SAM 是在 Trie 树上搞事情。

SAM 建立后缀树

在 SAM 的代码中，我们用到了几个数组，它们有对应的后缀树的含义：

数组	SAM	后缀树
$l e n_{u}$	$r o o t \to u$ 的最长路长度	原后缀树上 $u$ 的深度
$s i z_{u}$	$\| e n d p o s (u) \|$	$s u b t r e e (u)$ 中关键点个数
$l i n k_{u}$	$u$ 最长的包含类	$u$ 的父亲
$c h_{u, r}$	$δ (u, r)$	$r + u$ 在这棵 Trie 的位置

~~（注： $s i z_{u}$ 需要 dfs 预处理才有这个实际含义，其实它是 $u$ 的出现次数。）~~

如果想求得后缀树上 $u$ 下面那些儿子的边的第一个字母（或者叫后缀排序），请按以下方法执行：

建反串 SAM，记录 $p o s_{u}$ 表示 $u$ 这个等价类是在插入第 $i$ 个字符（先插入第 $n$ 个最后插第 $1$ 个）时建立的，split 的时候新的等价类的 $p o s$ 等于分裂那个。
连边： $l i n k_{u} \to^{S [p o s [u] + l e n [l i n k [u]]]} u$ ，连出来是棵树，证明很简单，你这个 $p o s [u]$ 相当于等价类 $u$ 的 $l e f t p o s$ 中的一个， $u$ 的最长串是 $S [p o s [u] + l e n [u] - 1]$ ，对应 $u$ 头上的；最短串是 $S [p o s [u] + l e n [l i n k [u]]]$ ，对应 $l i n k_{u}$ 底下的。

SAM 与后缀树的互换

其实可以这样说：正串 SAM 维护的是 $e n d p o s$ 或者 $r i g h t p o s$ ，反串 SAM 维护的是 $l e f t p o s$ ；正串 SAM 的 Link 树，往上跳的时候 $e n d p o s$ 变多，长度变短，砍掉了前缀，所以它可以认为是将所有前缀从右到左插入的 Trie（意思是对于一个前缀 $[1, i]$ ，从 $S [i]$ 开始向下插到 $S [1]$ ）；反串 SAM 的 Link 树，自然就是后缀树了。

各种自动机的比较

除了子序列自动机，我们现在见过的自动机有 ACAM（字符串匹配）、SAM（后缀自动机）、PAM（回文自动机）。它们的相同点是：状态转移集都形成一个 DAG。

自动机	状态集合	Link 树（若 $l i n k_{y} = x$ ）
SAM	原串的所有子串	则等价类 $x$ 是等价类 $y$ 的后缀
ACAM	所有字符串的前缀	则前缀 $x$ 是前缀 $y$ 的后缀
PAM	所有回文串	则回文子串 $x$ 是回文子串 $y$ 的后缀

简单应用

全都离不开 DAG 和 Link 树，二选一进行 DP 或匹配，甚至两个一起。基本子串结构将这些东西有机联合，见 https://www.cnblogs.com/crashed/p/17382894.html 对它的基本介绍。（据说原文是 2023 年许庭强论文）

两个后缀的 LCP

反串 SAM：后缀树上这两个后缀的 LCA 的深度。停停，怎么找这两个后缀？

for(int i=n;i>=1;i--) ap[i]=s.expand(a[i]-'a',ap[i+1]);

这样 $a p_{i}$ 就是 $[i, n]$ 这个后缀对应后缀树位置。

同理我们可以找到前缀的最长公共后缀：正着做一遍就是了。

求 $S [l, r]$ 子串在原串的出现次数

正串 SAM 上等价类的 $| e n d p o s |$ ，可以倍增。

具体说一下这个等价类怎么找： $S [l, r]$ ，首先取 $u$ 为插入 $S_{r}$ 时返回的那个等价类，在后缀链接上，我们要找到一个点 $p$ 使得 $l e n_{p} \geq r - l + 1$ （就是砍前缀，砍到它应该在的等价类）。然后取它的 $e n d p o s$ 大小就是答案了。

如果是反串 SAM 呢？反过来就行了。

int locate(int l,int r){
    int len=r-l+1,u=pos[r];
    for(int j=20;j>=0;j--) if(s.len[fa[j][u]]>=len) u=fa[j][u];
    return u;
}

本质不同的子串个数

这里注意到这个串是正串还是反串答案都不变。

SAM， $\sum_{u} l e n_{u} - l e n_{l i n k_{u}}$ 。

反串 SAM，原后缀树的每一个点对应一个子串，那么两个关键点之间的所有点加起来就是子串个数。
正串 SAM，每个等价类中最长长度为 $l e n_{u}$ ，最短长度为 $l e n_{l i n k_{u}} + 1$ （再短它的 $e n d p o s$ 增加，跳到上面），一共 $l e n_{u} - l e n_{l i n k_{u}}$ 个。对每个等价类分别计算。

SAM，DAG 上 DP，倒推， $f_{u} = 1 + \sum_{δ (u, v)} f_{v}$ 。

最小表示法

倍长并使用正串 SAM，即寻找 SAM 中字典序最小的长为 $| S |$ 的路径，DAG 上贪心走字典序最小的。

$S, T$ 的最长公共子串 / 字符串匹配

反串 SAM，建出 $S + # + T$ 的后缀树，~~求 dfn 序，求相邻两个不同字符串的后缀的 LCP~~。就是找一个点，使得它的子树中既有来自 $S$ 的又有来自 $T$ 的，使 $l e n$ 最大。这相当于是把 SA 搬到了树上。
考虑建出 $S$ 的正串 SAM，对 $T$ 的每个前缀求最大匹配，每次一点点地加入 $T_{i}$ ，动态更新当前走到的状态的长度，一直跳 Link 直到找到转移边就转移，取最优值即可。这相当于把 ACAM 的方法搬到了 SAM 上，比较相似。这里细说一下怎么匹配：动态维护 $u = 1, l = 0$ 初始，每次加入 $T$ 的字符 $r$ ，向上跳后缀链接找第一个 $δ (u, r)$ 存在的，同时如果跳了，则 $l$ 更新为新的 $l e n_{u}$ （没跳不更新）。然后如果存在 $δ (u, r)$ ，则 $u := δ (u, r), l := l + 1$ ；否则 $u = 1, l = 0$ 从头来过。注意 SAM 的匹配字符串一定要记录当前匹配的字符个数，因为一个等价类里的长度是不确定的。
考虑对 $S, T$ 建广义 SAM，那么我们就是要找最大的 $l e n_{u}$ 使得 $e n d p o s (u)$ 既有 $S$ 又有 $T$ 。

第二种方法就是字符串匹配，由此我们可以使用广义 SAM 薄纱 ACAM（虽然要乘个字符集是个大问题）

另外说一下怎么删字符，非常简单， $l := l - 1$ ，搞完之后如果不在这个等价类了（ $l = l e n_{l i n k_{u}}$ ），那么 $u = l i n k_{u}$ 。

例题 CF235C Cyclical Quest

本质不同第 $k$ 小子串

输出字符串

正串 SAM。我们将子串看作 DAG 上的一条路径，那么第 $k$ 小子串自然就是第 $k$ 小路径了。首先 DP 求出每个等价类 $u$ 能走出去多少条路径： $f_{u} = 1 + \sum_{v = δ (u, r)} f_{v}$ 。然后 dfs，到达等价类 $u$ 时，如果 $k = 1$ 那么就是它自己，输出；否则按字典序遍历它的转移，如果 $f_{v} < k$ 那么 $k := k - f_{v}$ ，否则 $d f s (v, k)$ 。这个 $k$ 是会变的。另外记得空串算一个串。

输出区间

对着 DAG 做链剖分，比较阴间，展开说说。考虑向重链剖分一样，对于每个点选出重儿子 $s o n_{u}$ ，使得它是所有出边（儿子）中 $f$ 最大的。考虑优化刚才 dfs 的过程，首先倍增跳重链，跳到 $k$ 不能再继续减，这时再跳轻边。这样的复杂度是 $O (n \log^{2} n)$ 的。

有一个例题 ABC280H 是没有本质相同的，有另外一种后缀数组做法，这里说的 SAM 做法也能过。（如果用下一节说的后缀排序还原后缀树那么可以线性遍历树，和后缀数组一样了）

点击查看代码

https://atcoder.jp/contests/abc280/submissions/43972309

void print(int u,int len){printf("%d %d %d\n",ep[u].first,ep[u].second-len+1,ep[u].second);}
void solve(int u,LL x,int len){
    for(int j=18;j>=0;j--) if(x>g[j][u]){
        if(x-g[j][u]<=f[to[j][u]]) x-=g[j][u],u=to[j][u],len+=1<<j;
    }
    if(x<=siz[u]) return print(u,len);
    x-=siz[u];
    for(int i=0;i<26;i++){
        int v=s.ch[u][i];
        if(x<=f[v]) return solve(v,x,len+1);
        else x-=f[v];
    }
}
void init(){
    m=s.tot;
    iota(p+1,p+m+1,1);
    sort(p+1,p+m+1,[&](int i,int j){return s.len[i]<s.len[j];});
    for(int j=m;j>=1;j--){
        int u=p[j]; int*ch=s.ch[u],son=0;
        siz[s.link[u]]+=siz[u],ep[s.link[u]]=ep[u],f[u]=siz[u];
        for(int i=0;i<26;i++) if(ch[i]) f[u]+=f[ch[i]];
        for(int i=0;i<26;i++) if(f[ch[son]]<f[ch[i]]) son=i;
        g[0][u]=siz[u],to[0][u]=ch[son];
        for(int i=0;i<son;i++) g[0][u]+=f[ch[i]];
    }
    for(int j=1;j<=18;j++){
        for(int i=1;i<=m;i++) to[j][i]=to[j-1][to[j-1][i]];
        for(int i=1;i<=m;i++) g[j][i]=g[j-1][i]+g[j-1][to[j-1][i]];
    }
}

询问的时候记得加 siz[1] 哦

后缀排序

那这位更是重量级，学会了可以薄纱后缀数组。方法就是还原后缀树。

建反串 SAM，记录 $p o s_{u}$ 表示 $u$ 这个等价类是在插入第 $i$ 个字符（先插入第 $n$ 个最后插第 $1$ 个）时建立的，split 的时候新的等价类的 $p o s$ 等于分裂那个。（实际上 $p o s_{u} = min {x | x \in s t a r t p o s (u)}$ ）
连边： $l i n k_{u} \to^{S [p o s [u] + l e n [l i n k [u]]]} u$ ，连出来是棵树。
dfs 树，按照边的字典序，先访问到的 $p o s$ 的后缀排序更前。
和 SA 一样求出 $h e i g h t$ 数组。

点击查看代码

https://uoj.ac/submission/646959

//split pos[u]=pos[q];
//expand pos[u]=now
void dfs(int u){
    if(key[u]) sa[rnk[pos[u]]=++cnt]=pos[u];
    for(int i=0;i<26;i++) if(to[u][i]) dfs(to[u][i]);
}
void gethei(){
    for(int i=1,k=0;i<=n;i++){
        if(rnk[i]==1) continue;
        int j=sa[rnk[i]-1]; k=max(k-1,0);
        while(max(i,j)+k<=n&&a[i+k]==a[j+k]) k++;
        hei[rnk[i]]=k;
    }
}
int main(){
    scanf("%s",a+1),n=strlen(a+1);
    for(int i=n,last=1;i>=1;i--) key[last=s.expand(a[i]-'a',last,i)]=1;
    for(int i=2;i<=s.tot;i++) to[s.link[i]][a[pos[i]+s.len[s.link[i]]]-'a']=i;
    dfs(1),gethei();
    for(int i=1;i<=n;i++) printf("%d%c",sa[i]," \n"[i==n]);
    for(int i=2;i<=n;i++) printf("%d%c",hei[i]," \n"[i==n]);
    return 0;
}

基本子串结构

https://www.cnblogs.com/caijianhong/p/18153828/solution-UOJ577

posted @ 2022-11-06 19:17 caijianhong 阅读(259) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· 【模板】广义后缀自动机 exSAM

· 【笔记】字符串选讲：ACAM、SAM 2024.8.1

· 后缀自动机学习笔记

· 后缀自动机 SAM

· 后缀自动机学习笔记

阅读排行：
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型，支持深度思考和联网搜索！
· 基于 Docker 搭建 FRP 内网穿透开源项目（很简单哒）
· ollama系列01：轻松3步本地部署deepseek，普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现

公告

日记文章

密码是那位老师的名言。

昵称： caijianhong
园龄： 2年4个月
粉丝： 61
关注： 28

+加关注

2025年3月

日

一

二

三

四

五

六

合集

短文新编(31)

随笔分类

随笔档案

相册

OI(54)

【模板】后缀自动机 SAM、后缀树、广义后缀自动机

后缀自动机

概念

构造（理解一）

构造（理解二）

广义 SAM 相关

code

后缀树

SAM 与后缀树的联系

SAM 建立后缀树

SAM 与后缀树的互换

各种自动机的比较

简单应用

两个后缀的 LCP

求 $S [l, r]$ 子串在原串的出现次数

本质不同的子串个数

最小表示法

$S, T$ 的最长公共子串 / 字符串匹配

本质不同第 $k$ 小子串

输出字符串

输出区间

后缀排序

基本子串结构

公告

搜索

常用链接

我的标签

合集

随笔分类

随笔档案

相册

阅读排行榜

评论排行榜

推荐排行榜

最新评论

【模板】后缀自动机 SAM、后缀树、广义后缀自动机

后缀自动机

概念

构造（理解一）

构造（理解二）

广义 SAM 相关

code

后缀树

SAM 与后缀树的联系

SAM 建立后缀树

SAM 与后缀树的互换

各种自动机的比较

简单应用

两个后缀的 LCP

求 S[l,r] 子串在原串的出现次数

本质不同的子串个数

最小表示法

S,T 的最长公共子串 / 字符串匹配

本质不同第 k 小子串

输出字符串

输出区间

后缀排序

基本子串结构

公告

搜索

常用链接

我的标签

合集

随笔分类

随笔档案

相册

阅读排行榜

评论排行榜

推荐排行榜

最新评论

求 $S [l, r]$ 子串在原串的出现次数

$S, T$ 的最长公共子串 / 字符串匹配

本质不同第 $k$ 小子串