【模板】后缀数组 SA
posted on 2022-08-07 17:04:40 | under 模板 | source
\(LCP(S, T)\) 是两个字符串 \(S, T\) 的最长公共前缀(The Longest Common Prefix)。
模板:0-index 字符串 LCP 后缀数组实现(完全 vector)
vector::push_back有性能问题,原因未知,直接使用vec[++tot]。for (int j = 1; j <= n; j <<= 1)顶到 \(n\) 以防止 \(n=1\) 时 \(rk\) 求错__lg(n)与31 - __builtin_clz(n)一样快。
struct machine {// {{{
int n;
vector<int> rk, sa, st[30], buc, id;
machine() = default;
explicit machine(const string& str)
: n((int)str.size()), rk(n + 1), sa(n), buc(max(n, 128)), id(n) {
rk[n] = -1;
for (int i = 0; i < n; i++) buc[rk[i] = str[i]] += 1;
for (int i = 1; i < 128; i++) buc[i] += buc[i - 1];
for (int i = n; i--;) sa[--buc[rk[i]]] = i;
for (int j = 1; j <= n; j <<= 1) {
int cur = 0;
for (int i = n - j; i < n; i++) id[cur++] = i;
for (int i = 0; i < n; i++)
if (sa[i] >= j) id[cur++] = sa[i] - j;
memset(buc.data(), 0, sizeof(int) * n);
for (int i = 0; i < n; i++) buc[rk[i]] += 1;
for (int i = 1; i < n; i++) buc[i] += buc[i - 1];
for (int i = n; i--;) sa[--buc[rk[id[i]]]] = id[i];
id[0] = 0;
auto pred = [&](int x, int y) {
return rk[x] != rk[y] || rk[x + j] != rk[y + j];
};
int pre = id[sa[0]] = 0;
for (int i = 1; i < n; i++) id[sa[i]] = (pre += pred(sa[i - 1], sa[i]));
memcpy(rk.data(), id.data(), sizeof(int) * n);
if (pre + 1 == n) break;
}
auto& lcp = st[0];
lcp.resize(n - 1);
for (int i = 0, h = 0; i < n; i++) {
if (!rk[i]) continue;
if (h) h -= 1;
int j = sa[rk[i] - 1];
while (max(i, j) + h < n && str[i + h] == str[j + h]) h += 1;
lcp[rk[i] - 1] = h;
}
for (int j = 1; 1 << j <= n; j++) {
st[j].resize(n - (1 << j));
for (int i = 0; i + (1 << j) < n; i++) {
st[j][i] = min(st[j - 1][i], st[j - 1][i + (1 << (j - 1))]);
}
}
}
int operator()(int i, int j) const {
if (max(i, j) == n) return 0;
if (i == j) return n - i;
int l = min(rk[i], rk[j]), r = max(rk[i], rk[j]) - 1;
int k = __lg(r - l + 1);
return min(st[k][l], st[k][r - (1 << k) + 1]);
}
};// }}}
后缀数组
简单来说,后缀数组需要一个长为 \(n\) 的字符串 \(S\),它求出了:
- \(sa_i\),将 \(S\) 的所有真后缀按字典序排序,排在第 \(i\) 位的后缀(的起始点,显然 \(1\leq sa_i\leq n\),以下默认如此)。
- \(rnk_i\),第 \(i\) 个后缀的排名,显然有 \(rnk_{sa_i}=i\)。
- \(hei_i\),为 \(lcp(i-1,i)\),即排序后第 \(i\) 小后缀和第 \(i-1\) 小后缀的最长公共前缀。此处 \(lcp(i,j)=LCP(S[sa_i,n],S[sa_j,n])\),即这两个后缀的 LCP。
实现时使用倍增,令当前的排序长度为 \(2^j\),每次将上一轮的 \(rnk\) 合并在一起就可以比较两个(第 \(i\) 个后缀可以被 \((rnk_i,rnk_{i+2^{j-1}})\) 表示,从而可以 \(O(1)\) 比较)。使用桶排序,总复杂度 \(O(n\log n)\)。
对于 \(hei_i\) 数组,我们求一个 \(h_i=hei_{rnk_i}\)(\(h_i\) 表示后缀 \(S[i, n]\) 与其在 \(sa\) 中上一位的后缀的 LCP),由题解得 \(h_{i-1}-1\leq h_i\),于是考虑像 manacher 一样维护算出 \(h_i\),进而得到 \(hei_i\)。显然是线性复杂度 \(O(n)\)。
code
点击查看代码
template <int N, int M = 128>
struct SA {
int sa[N + 10], rnk[N + 10], h[N + 10], hei[N + 10];
void bucketsort(int n) {
memset(hei, 0, sizeof hei);
for (int i = 1; i <= n; i++) hei[rnk[h[i]]]++;
for (int i = 1; i <= max(n, M); i++) hei[i] += hei[i - 1];
for (int i = n; i >= 1; i--) sa[hei[rnk[h[i]]]--] = h[i];
}
void build(char *s) {
int n = strlen(s + 1);
rnk[n + 1] = 0;
for (int i = 1; i <= n; i++) h[i] = i, rnk[i] = s[i];
bucketsort(n);
for (int j = 1; j <= n; j <<= 1) {
int tot = 0;
for (int i = n - j + 1; i <= n; i++) h[++tot] = i;
for (int i = 1; i <= n; i++)
if (sa[i] - j > 0) h[++tot] = sa[i] - j;
bucketsort(n);
tot = h[sa[1]] = 1;
for (int i = 2; i <= n; i++)
h[sa[i]] =
rnk[sa[i - 1]] == rnk[sa[i]] && rnk[sa[i - 1] + j] == rnk[sa[i] + j]
? tot
: ++tot;
memcpy(rnk, h, sizeof h);
}
memset(hei, 0, sizeof hei);
for (int i = 1, k = 0; i <= n; i++) {
if (rnk[i] == 1) continue;
int j = sa[rnk[i] - 1];
k = max(k - 1, 0);
while (max(i, j) + k <= n && s[i + k] == s[j + k]) k++;
hei[rnk[i]] = k;
}
}
};
点击查看代码
int n, sa[50010], rnk[50010], hei[50010];
char a[50010];
namespace suffixsa {
void getsa() {
static int tmp[50010];
auto bucketsort = [&](int v) {
auto& buc = hei;
for (int i = 0; i <= v; i++) buc[i] = 0;
for (int i = 1; i <= n; i++) buc[rnk[tmp[i]]] += 1;
for (int i = 1; i <= v; i++) buc[i] += buc[i - 1];
for (int i = n; i >= 1; i--) sa[buc[rnk[tmp[i]]]--] = tmp[i];
};
for (int i = 1; i <= n; i++) tmp[i] = i, rnk[i] = a[i];
bucketsort(128);
rnk[n + 1] = 0;
for (int j = 1; j <= n; j <<= 1) {
int cnt = 0;
for (int i = n - j + 1; i <= n; i++) tmp[++cnt] = i;
for (int i = 1; i <= n; i++)
if (sa[i] > j) tmp[++cnt] = sa[i] - j;
bucketsort(n);
cnt = tmp[sa[1]] = 1;
for (int i = 2; i <= n; i++) {
if (rnk[sa[i - 1]] != rnk[sa[i]] || rnk[sa[i - 1] + j] != rnk[sa[i] + j])
cnt += 1;
tmp[sa[i]] = cnt;
}
for (int i = 1; i <= n; i++) rnk[i] = tmp[i];
}
}
void getlcp() {
int h = 0;
hei[1] = 0;
for (int i = 1; i <= n; i++) {
if (rnk[i] == 1) continue;
int j = sa[rnk[i] - 1];
if (h) h -= 1;
while (max(i, j) + h <= n && a[i + h] == a[j + h]) h += 1;
hei[rnk[i]] = h;
}
}
}; // namespace suffixsa
点击查看代码(完全 vector)
vector<int> get_sa(const string& a) {
int n = a.size();
vector<int> sa(n), rk(a.begin(), a.end()), h(n);
auto bucketsort = [&](const auto& key) {
vector<int> buc(max(n, 128));
reverse(h.begin(), h.end());
for (int i : h) buc[rk[i]] += 1;
partial_sum(buc.begin(), buc.end(), buc.begin());
for (int i : h) sa[--buc[rk[i]]] = i;
vector<int> tmp(n);
tmp[sa[0]] = 0;
for (int i = 1; i < n; i++) tmp[sa[i]] = tmp[sa[i - 1]] + (key(sa[i - 1]) != key(sa[i]));
rk = move(tmp);
};
for (int i = 0; i < n; i++) h[i] = i;
bucketsort([&](int x) { return rk[x]; });
for (int j = 1; j < n; j <<= 1) {
h.clear();
for (int i = n - j; i < n; i++) h.push_back(i);
for (int i = 0; i < n; i++) if (sa[i] >= j) h.push_back(sa[i] - j);
bucketsort([&](int x) { return make_pair(rk[x], x + j < n ? rk[x + j] : -1); });
}
return sa;
}
vector<int> get_lcp(const string& a, const vector<int>& sa) {
int n = a.size();
vector<int> rk(n), lcp(n - 1);
for (int i = 0; i < n; i++) rk[sa[i]] = i;
for (int i = 0, h = 0; i < n; i++) {
if (!rk[i]) continue;
if (h) h -= 1;
int j = sa[rk[i] - 1];
while (max(i, j) + h < n && a[i + h] == a[j + h]) h += 1;
lcp[rk[i] - 1] = h;
}
return lcp;
}
证明 \(rnk_{sa_i+j}\) 只会越界到 \(n+1\)
您写出了这个代码,发现您的 \(rnk\) 开了一倍且写出了 rnk[sa[i-1]+j]==rnk[sa[i]+j] 这样的东西,这不会越界吗?
证明
定义一个空字符为 \(0\),且不与其它任何字符相同。
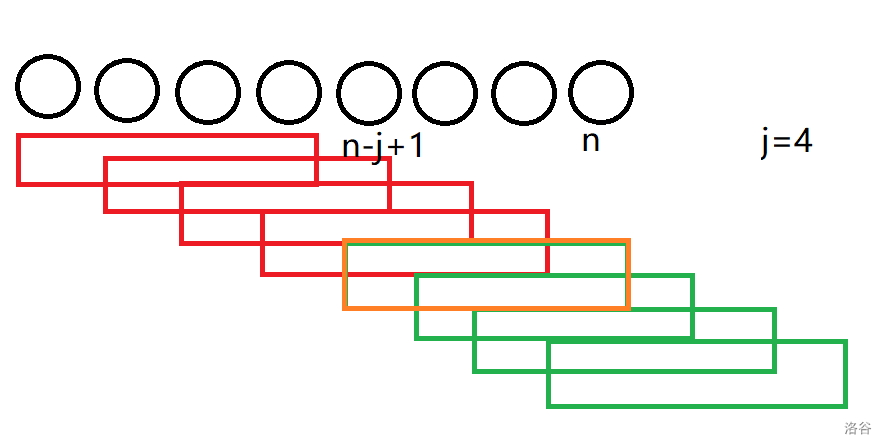
假设我们枚举到 \(n=8,j=4\),分类讨论:
- 有三个后缀(绿色)超出了原串范围。但是,这些后缀的 \(rnk\) 互不相同,你找不到其它任何一个后缀和它们相等,因为空字符和其它字符都不相同,所以
rnk[sa[i-1]]==rnk[sa[i]]必然不成立,&&立即短路,不会越界。 - 有一个刚好到达串尾的后缀(橙色)看起来很危险,它有可能和前面一个后缀相等,但是它的起始位置是 \(n-j+1\),右移 \(j\) 位是 \(n+1\),只会越界到 \(n+1\),因此我们只需要初始化 \(rnk_{n+1}=0\) 即可。
- 剩余的四个后缀没有超出原串范围(红色),没有越界风险。
归纳证明,易得其它情况亦成立,故 \(rnk_{sa_i+j}\) 只会越界到 \(n+1\),原命题得证。
解决方法
由上文得,我们只需要令 \(rnk_{n+1}=0\)。保险起见,你的字符集最好不要出现 \(0\)。
构造数据
只需要一个长为 \(2^j\) 的后缀,它在原串的出现次数大于一,就会出现以上情况。一个形如 aaaaaaa......aaa 或 ababababab......ababab 可以尽量多地卡到上限。
求两个后缀的 LCP
性质:有相同前缀的后缀,在 \(sa\) 中是一段连续区间。
LCP Lemma:\(lcp(i,j)=\min\limits_{i\leq k\leq j}\{lcp(i,k),lcp(k,j)\}\)。
LCP Theorem:\(lcp(i,j)=\min\limits_{i<k\leq j}lcp(k-1,k)=\min\limits_{i<k\leq j}hei_k\)。
于是问题变为在 \(hei_i\) 上做 RMQ(\(hei[rnk_l+1,rnk_r]\) 的最小值)。使用 ST 表可以做到 \(O(n\log n)-O(1)\)。
求 \(S[l,r]\) 在原串的出现次数
性质:有相同前缀的后缀,在 \(sa\) 中是一段连续区间。
性质:\(S[l,r]\) 等价于 \(S[l,n]\) 这个后缀的一段长为 \(r-l+1\) 的前缀。
考虑在 \(sa\) 中找到 \(S[l,n]\) 这段后缀(\(rnk_l\)),在左/右两边分别二分出最小/大的 \(x,y\),使 \(lcp(x,rnk_l)\geq r-l+1\),\(lcp(rnk_l,y)\geq r-l+1\)(这样 \([x,y]\) 区间都有了这一段前缀),与 0x01 的 LCP 求法类似,复杂度 \(O(n\log n)-O(\log n)\)。
本质不同的子串个数(位置不同算相同)
Recall:\(hei_i\),为 \(lcp(i-1,i)\),即排序后第 \(i\) 小后缀和第 \(i-1\) 小后缀的最长公共前缀。
考虑又一次把子串看成后缀的前缀,在 \(sa\) 意义下,后缀 \(sa_i\) 的长度为 \(n-sa_i+1\),这些都是可以统计的子串。但是,有一些子串是重复算的,有 \(hei_i\) 个前缀一定在上一个 \(sa_{i-1}\) 计算过了,于是我们要求的其实是:
复杂度 \(O(n\log n)\)。
循环同构的最小表示法
最小表示法:字符串 \(S\) 的所有循环同构中,字典序最小的。
考虑倍长原串,这样 \(S\) 的循环同构就能表示成 \(S[i,i+n-1] (1\leq i\leq n)\),对它做后缀排序,取 \(sa\) 中最小的在 \([1,n]\) 范围内的后缀(多那么一点不影响答案),这就是 \(S\) 的最小表示法。复杂度 \(O(n\log n)\)。
\(S,T\) 的最长公共子串
考虑造一个串 \(R=S+\text{'\#'}+T\),求出它的后缀数组,于是有一个 naive 的想法:求出任意两个后缀的 \(LCP\)。但很显然是假的。
众所周知,前缀 \(\min\) 有单调性,于是我们可以贪心的选两个(在 \(sa\) 中)相邻的后缀,它们的 \(LCP\) 一定最优。但是!如果你取两个都来自 \(S\) 的前缀,那就寄了,想象一个把 \(S\) 的后缀染成白色,\(T\) 的后缀染成黑色,我们应该统计的是,在 \(sa\) 中,两个相邻的异色的后缀,的 \(LCP\)(即 \(hei\))。复杂度 \(O(n\log n)\)。
判定后缀数组
有字符串 \(s\) 和后缀数组排列 \(p\),令 \(p_0=n+1\),\(s_{n+1}\) 小于 \(s\) 中其它字符。则 \(p\) 为 \(s\) 的后缀数组 \(\iff\) 对于所有 \(i\),在 \(p\) 上:
- 若 \(p_i+1\) 在 \(p_{i+1}+1\) 之前,则要求 \(s_i\leq s_{i+1}\)。
- 若 \(p_i+1\) 在 \(p_{i+1}+1\) 之后,则要求 \(s_i< s_{i+1}\)。
本文来自博客园,作者:caijianhong,转载请注明原文链接:https://www.cnblogs.com/caijianhong/p/template-suffix-array.html


