【模板】多项式乘法 FFT/NTT

posted on 2022-08-02 23:57:12 | under 模板 | source
膜拜，抄写

20230807 修改。删除偏激语言，所有 \(i\) 换成 \(\mathrm i\)，所有 \(w\) 换成 \(\omega\)，增加证明。

模板（modint<998244353>, version 2）

预处理 23 个单位根会快很多很多

typedef modint<998244353> mint;
const int glim(const int &x){return 1 << (32 - __builtin_clz(x));}
const int bitctz(const int &x){return __builtin_ctz(x);}
const vector<mint> wns = []() -> vector<mint> {
    vector<mint> wns = {};
    for (int j = 1; j <= 23; j++)
        wns.push_back(qpow(mint(3), raw(mint(-1)) >> j));
    return wns;
}();
void ntt(vector<mint> &a, const int &op) {
    const int n = a.size();
    for (int i = 1, r = 0; i < n; i++) {
        r ^= n - (1 << (bitctz(n) - bitctz(i) - 1));
        if (i < r) swap(a[i], a[r]);
    }
    vector<mint> w(n);
    for (int k = 1, len = 2; len <= n; k <<= 1, len <<= 1) {
        const mint wn = wns[bitctz(k)];
        for (int i = raw(w[0] = 1); i < k; i++) w[i] = w[i - 1] * wn;
        for (int i = 0; i < n; i += len) {
            for (int j = 0; j < k; j++) {
                const mint x = a[i + j], y = a[i + j + k] * w[j];
                a[i + j] = x + y, a[i + j + k] = x - y;
            }
        }
    }
    if (op == -1) {
        const mint iz = mint(1) / n;
        for (int i = 0; i < n; i++) a[i] *= iz;
        reverse(a.begin() + 1, a.end());
    }
}

模板（modint<998244353>, version 1）

int glim(int x){return 1<<(32-__builtin_clz(x));}
int bitctz(int x){return __builtin_ctz(x);}
const int P=998244353,G=3;
typedef modint<998244353> mint;
void ntt(vector<mint>&a,int op){
	int n=a.size(); vector<mint> w(n);
    for(int i=1,r=0;i<n;i++){
        int b=bitctz(n)-bitctz(i);
        r&=(1<<b)-1,r^=1<<(b-1);
        if(i<r) swap(a[i],a[r]);
    }
	for(int k=1,len=2;len<=n;k<<=1,len<<=1){
		mint wn=qpow(op==1?mint(G):mint(1)/G,(P-1)/len);
		for(int i=raw(w[0]=1);i<k;i++) w[i]=w[i-1]*wn;
		for(int i=0;i<n;i+=len){
			for(int j=0;j<k;j++){
				mint x=a[i+j],y=a[i+j+k]*w[j];
				a[i+j]=x+y,a[i+j+k]=x-y;
			}
		}
	}
	if(op==-1){mint inv=mint(1)/n; for(mint&x:a) x*=inv;}
}

模板（LL）

typedef long long LL;
LL qpow(LL a,LL b,int p){LL r=1;for(a%=p;b;b>>=1,a=a*a%p) if(b&1) r=r*a%p; return r;}
const int P=998244353,G=3,G0=qpow(G,P-2,P);
LL mod(LL x){return (x%P+P)%P;}
void red(LL&x){x%=P;}
vector<LL> ntt(vector<LL> a,int op){
	int n=a.size(); vector<LL> w(n);
	for(int i=1;i<n;i++) w[i]=w[i>>1]>>1|(i&1?n>>1:0);
	for(int i=0;i<n;i++) if(i<w[i]) swap(a[i],a[w[i]]);
	for(int k=1,len=2;len<=n;k<<=1,len<<=1){
		LL wn=qpow(op==1?G:G0,(P-1)/len,P);
		for(int i=w[0]=1;i<k;i++) red(w[i]=w[i-1]*wn);
		for(int i=0;i<n;i+=len){
			for(int j=0;j<k;j++){
				LL x=a[i+j]%P,y=a[i+j+k]*w[j]%P;
				a[i+j]=x+y,a[i+j+k]=x-y;
			}
		}
	}
	for(LL&x:a) x=mod(x);
	if(op==-1){LL inv=qpow(n,P-2,P); for(LL&x:a) red(x*=inv);}
	return a;
}
vector<LL> multiple(vector<LL> a,const vector<LL>&b){
	for(int i=0,len=a.size();i<len;i++) red(a[i]*=b[i]);
	return a;
}

暴力对拍

vector<mint> multiple(const vector<mint> &a, const vector<mint> &b) {
    if (a.empty()) return b;
    if (b.empty()) return a;
    vector<mint> c(a.size() + b.size() - 1);
    for (int i = 0; i < a.size(); i++) {
        for (int j = 0; j < b.size(); j++) {
            c[i + j] += a[i] * b[j];
        }
    }
    return c;
}
vector<mint> add(const vector<mint> &a, const vector<mint> &b) {
    vector<mint> c(max(a.size(), b.size()));
    for (int i = 0; i < a.size(); i++) c[i] += a[i];
    for (int i = 0; i < b.size(); i++) c[i] += b[i];
    return c;
}

闲话

为什么你看不懂 FFT？自查：

推不出单位根的三条性质：重新理解“模长相乘，辐角相加”的含义，以及，拿单位根的几何意义去证明。
不想看公式：没救了，放一会吧。

保存：https://www.luogu.com.cn/blog/cch/xun-huan-ju-zhen-xing-lie-shi
https://www.cnblogs.com/ac-evil/p/14734728.html

问题

\(c_k=\sum_{i+j=k}a_ib_j\)。\(a,b\) 已知，要求 \(O(n\log n)\)。另一种表示是将两个多项式相乘，求出相乘后多项式的各项系数。

复数

定义

一个复数 \(z=a+b\mathrm i\) 其中 \(\mathrm i^2=-1\)。我们可以把 \(z=a+b\mathrm i\) 当作平面直角坐标系（这时它升级成复平面）中的一个点 \((a,b)\)，还可以把它当作一个向量 \((a,b)\)，这三者是一一对应的。

我们可以定义这个复数的模长 \(|z|=\sqrt{a^2+b^2}\) 为它到原点的距离，~~和向量一模一样~~。

它的辐角为 \(\theta=\arctan\left(\frac{b}{a}\right)\)，即与 \(x\) 轴的夹角（\(x\) 轴转到 \(z\) 的角），~~与向量一模一样~~。

全体复数构成的数域记为 \(\mathbb C\)。

运算法则

加减法：\((a_1+b_1\mathrm i)\pm(a_2+b_2\mathrm i)=(a_1\pm a_2)+(b_1\pm b_2)\mathrm i\)。满足平行四边形法则。

乘法：这里和向量有点区别，复数乘复数还是复数，我们首先看代数方面：\((a_1+b_1\mathrm i)\cdot(a_2+b_2\mathrm i)=(a_1a_2-b_1b_2)+(a_1b_2+a_2b_1)\mathrm i.\)

然后是几何方面：模长相乘，辐角相加。（重要）

补个证明：设复数 \(z_1=\ell_1 e^{\mathrm i\alpha}\)（由欧拉公式 \(e^{\mathrm ix}=\cos x+\mathrm i\sin x\) 得，每个形如 \(z=a+b\mathrm i\) 的复数可以表示为 \(\ell e^{\pi\theta}\)，如这个 \(z_1\) 实际上就是 \(\ell_1\cos\alpha+\ell_1\sin\alpha\mathrm i\)，这里 \(\ell_1\) 就是模长，\(\alpha\) 就是辐角），同理另一个 \(z_2=\ell_2 e^{\mathrm i\beta}\)，乘起来就是 \(\ell_1\ell_2 e^{\mathrm i(\alpha+\beta)}\)。证毕。

除法丢个式子吧：

\[\dfrac{a_1+b_1\mathrm i}{a_2+b_2\mathrm i}=\frac{(a_1+b_1\mathrm i)(a_2-b_2\mathrm i)}{(a_2+b_2\mathrm i)(a_2-b_2\mathrm i)}=\frac{(a_1a_2+b_1b_2)+(-a_1b_2+a_2b_1)\mathrm i}{a_2^2+b_2^2}=\frac{(a_1a_2+b_1b_2)}{a_2^2+b_2^2}+\frac{-a_1b_2+a_2b_1}{a_2^2+b_2^2}\mathrm i. \]

共轭复数

一个复数 \(z=a+b\mathrm i\) 的共轭复数为 \(\overline{z}=a-b\mathrm i\)（实部不变，虚部取反）。

若 \(|z|=1\)，这时它与它的共轭复数互为倒数。证明就是在单位圆上绕了一圈回来。

单位圆、单位根

将复平面上的一个单位圆等分成 \(n\) 份，记其中一份为 \(\omega_n=(\cos\frac{2\pi}{n},\sin\frac{2\pi}{n})\)。我们贺个图吧：

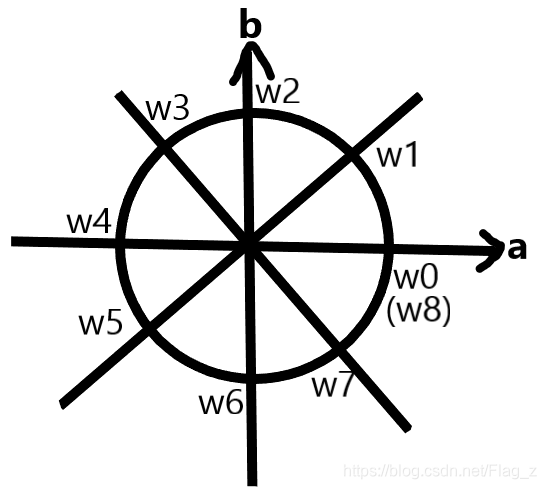
图中 \(w2,w3\) 代表 \(\omega_8^2,\omega_8^3\)，请注意这里 \(\omega_8^2\) 表示 \((\omega_8)^2\)。你可以认为，从 \(\omega_8^i\) 到 \(\omega_8^{i+1}\)，相当于是乘了一个 \(\omega_8\)，转了一个扇形。

我们寻找一些重要性质：

\(\omega_n^0,\omega_n^1,\omega_n^2,\cdots,\omega_n^{n-1}\) 互不相同。
\(\omega_n^0=\omega_n^n=1\)：转回来了。
\(\omega_n^k=\omega_{2n}^{2k}\)：在分为 \(2n\) 份的圆上一次跳两步。
\(\omega_n^k=-\omega_n^{k+n/2}\)：转了半圈转到相反数。

多项式乘法

两个多项式 \(A,B\) 按照代数意义相乘，有什么好的做法吗？

一种做法是，找到 \(n\) 个互不相同的值 \(x_0,x_1,x_2,\cdots\) 代入 \(A,B\) 求值，将这两个多项式的值对应位相乘，再反代回去。请注意这里 \(n\) 是两个多项式的最高次数的和加一。

为什么正确呢？因为 \(n\) 个点能唯一插出一个 \(n-1\) 次多项式，反过来也如此。

这就是所谓的系数表示法和点值表示法的互换。注意到点值表示法相乘为 \(O(n)\)，我们可以试图优化一下两种方法之间的互换。

快速傅里叶变换：FFT

铺垫这么久我们还是不会多项式乘法，怎么办呢？

伟大的数学家傅里叶在 \(A,B\) 中代入了 \(n\) 个 \(n\) 次单位根，并说这有很好的性质，我们开始研究这有什么性质。

离散傅里叶变换：DFT

什么是 DFT？系数表示法转点值表示法。

我们就只看一个多项式 \(F(x)\)，现在要代入 \(n\) 个单位根求值。

将 \(F\) 按下标奇偶分为两类：例如 \(F(x)=f_0x^0+f_1x^1+f_2x^2+f_3x^3+\cdots\)，我们拆成 \(F_0(x)=f_0x^0+f_2x^1+f_4x^2+\cdots\) 和 \(F_1(x)=f_1x^0+f_3x^1+f_5x^2+\cdots\)。那么 \(F(x)=F_0(x^2)+xF_1(x^2)\)。

我们递归下去，假设我们已知 \(F_0(\omega_{n/2}^0),F_0(\omega_{n/2}^1),\cdots,F_0(\omega_{n/2}^{n/2-1})\) 与 \(F_1(\omega_{n/2}^0),F_1(\omega_{n/2}^1),\cdots,F_1(\omega_{n/2}^{n/2-1})\).

考虑 \(F(\omega_n^k)\)，其中 \(0\leq k<n/2\)，我们开始利用信息：

\[\begin{aligned} F(\omega_n^k)&=F_0((\omega_n^k)^2)+\omega_n^k\cdot F_1((\omega_n^k)^2)\\ &=F_0(\omega_n^{2k})+\omega_n^k\cdot F_1(\omega_n^{2k})\\ &=F_0(\omega_{n/2}^k)+\omega_n^k\cdot F_1(\omega_{n/2}^k)\\ \end{aligned} \]

这些东西都求过了可以直接用，那么 \(k\geq n/2\) 呢？

\[\begin{aligned} F(\omega_n^{k+n/2})&=F_0((\omega_n^{k+n/2})^2)+\omega_n^{k+n/2}\cdot F_1((\omega_n^{k+n/2})^2)\\ &=F_0(\omega_n^{2k+n})+\omega_n^{k+n/2}\cdot F_1(\omega_n^{2k+n})\\ &=F_0(\omega_{n/2}^{k+n/2})-\omega_n^k\cdot F_1(\omega_{n/2}^{k+n/2})\\ &=F_0(\omega_{n/2}^k)-\omega_n^k\cdot F_1(\omega_{n/2}^k)\\ \end{aligned} \]

啊这很好这些东西都是可求的，考虑时间复杂度 \(T(n)=2T(n/2)+O(n)=O(n\log n)\) 我们完成了 DFT。

逆离散傅里叶变换：IDFT

什么是 IDFT？点值表示法转系数表示法。

方法先给：代入所有单位根的倒数 \(\omega_n^0,\omega_n^{-1},\omega_n^{-2},\cdots,\omega_n^{1-n}\) 做 DFT，然后求出来的东西除以 \(n\) 就说是系数。

证明？

考虑对于多项式 \(F(x)=\sum_{0\leq i<n}f_ix^i\) 我们刚刚 DFT 出了 \(n\) 个点值 \(y_0,y_1,\cdots,y_{n-1}\)，将这些点值看作新的多项式 \(G(x)=\sum_{i<n}y_ix^i\)，然后代入单位根的倒数，考虑求出来的“点值”记为 \(z_i\) 我们看一看：

\[\begin{aligned} z_k&=\sum_{0\leq i<n}y_i(\omega_n^{-k})^i\\ &=\sum_{0\leq i<n}(\sum_{0\leq j<n}f_j(\omega_n^i)^j)(\omega_n^i)^{-k}\\ &=\sum_{0\leq j<n}f_j\sum_{0\leq i<n}(\omega_n^i)^{j-k}. \end{aligned} \]

若 \(j=k\Rightarrow j-k=0\) 则有 \(\sum_{0\leq i<n}(\omega_n^i)^{j-k}=n\) 挺好。

否则根据等比数列求和公式有 \(\sum_{0\leq i<n}(\omega_n^i)^{j-k}=\frac{(\omega_n^{j-k})^n-1}{\omega_n^{j-k}-1}=\frac{(\omega_n^n)^{j-k}-1}{\omega_n^{j-k}-1}=\frac{1-1}{?}=0\)。（\(\omega_n^n=1\)）

回头看看 \(j,k\) 是什么？是不是说 \(z_k=f_j\cdot n\)，移项一下就是答案了。

单位根反演：\([n|k]=\frac{1}{n}\sum_{i=0}^{n-1}\omega^{ik}\)。其中 \(\omega^n=1\)。证明上述。

至此我们终于完成了 FFT：dft(a),dft(b),multiple(a,b,c),idft(c)。

位逆序置换

我们观察一下所谓的按奇偶分类是什么东西：

第一层	000	001	010	011	100	101	110	111
第二层	000	010	100	110	001	011	101	111
第三层	000	100	010	110	001	101	011	111

大眼观察可得第一层和第三层的关系就是在二进制下翻转，于是我们可以先把它们放到正确的位置，然后从下往上做迭代 FFT。

另外有个细节：FFT 要求每一层都平分，那么我们一上来就把它补齐成 \(2^k\) 的形式就好。

注意这里的补齐，如果多项式 \(A,B\) 的次数分别为 \(n,m\)，那么补齐的 \(2^k\) 必须 \(>n+m+1\)。

因为，\(n\) 个点值唯一确定 \(n-1\) 次多项式，唯一确定 \(n\) 项的系数，唯一确定一个 \(\pmod {x^n}\) 的多项式。

code：FFT

点击查看代码

#include <cmath>
#include <cstdio>
#include <cstring>
#include <complex>
#include <algorithm>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr,##__VA_ARGS__)
#else
#define debug(...) void(0)
#endif
typedef long long LL;
typedef complex<double> comp;
const double PI=acos(-1);
int n,m,lim,rev[1<<21];
complex<double> a[1<<21],b[1<<21];
void fft(complex<double> a[],int n,int op){
	for(int i=0;i<n;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
	for(int len=2,k=1;len<=n;len<<=1,k<<=1){
		complex<double> wn(cos(PI/k),op*sin(PI/k));
		for(int i=0;i<n;i+=len){
			complex<double> w(1,0);
			for(int j=0;j<k;j++,w*=wn){
				complex<double> x=a[i+j],y=w*a[i+j+k];
				a[i+j]=x+y,a[i+j+k]=x-y;
			}
		}
	}
	if(op==-1) for(int i=0;i<n;i++) a[i]/=n;
}
int main(){
//	#ifdef LOCAL
//	 	freopen("input.in","r",stdin);
//	#endif
	scanf("%d%d",&n,&m);
	for(lim=1;lim<=n+m;lim<<=1);
	for(int i=0;i<lim;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(__lg(lim)-1));
	for(int i=0,x;i<=n;i++) scanf("%d",&x),a[i]=x;
	for(int i=0,x;i<=m;i++) scanf("%d",&x),b[i]=x;
	fft(a,lim,1),fft(b,lim,1);
	for(int i=0;i<lim;i++) a[i]*=b[i];
	fft(a,lim,-1);
	for(int i=0;i<=n+m;i++) printf("%d%c",(int)(a[i].real()+0.5)," \n"[i==n+m]);
	return 0;
}

FFT 三次变两次优化

欲将计算 \(A\times B\)，我们可以构造多项式 \(F(x)=\sum_{i<n}(a_i+b_i\text{i})x^i\)，就是把 \(b\) 放到虚部上。

然后计算 \(F(x)^2\)，取出虚部除以二就是答案。证明：

\[(a+b\mathrm i)^2=(a^2-b^2)+(2ab\mathrm i). \]

快速数论变换：NTT

~~欲将学习 NTT，首要的任务是学习 FFT，因为这些性质还是要用单位根证明（）~~

NTT 就是说在所有系数 \(\pmod P\) 意义下进行 FFT，那这时没有复数了怎么办呢？

引入原根：在 \(\pmod P\) 意义下，若有一个 \(g\)，满足 \(g^0,g^1,g^2,\cdots,g^{P-2}\) 都互不相同，则说 \(g\) 是 \(P\) 的原根。（更加准确的定义是模 \(P\) 的阶为 \(\varphi(P)\) 的数是原根）

常用的 NTT 模数：\(998244353=119\times 2^{23}+1,1004535809=479\times 2^{21}+1\)，两者原根都为 \(3\)。

我们说，FFT 中的 \(\omega_n=g^{\frac{P-1}{n}}\)。下面证明一下 FFT 的四个性质是否成立：

Recall：单位根四个性质

\(\omega_n^0,\omega_n^1,\omega_n^2,\cdots,\omega_n^{n-1}\) 互不相同。
\(\omega_n^0=\omega_n^n=1\)：转回来了。
\(\omega_n^k=\omega_{2n}^{2k}\)：在分为 \(2n\) 份的圆上一次跳两步。
\(\omega_n^k=-\omega_n^{k+n/2}\)：转了半圈转到相反数。

以下令 \(P=q_n\times n+1\) 其中我们用到的 \(n=2^k\)（\(q_n,k\) 都不一定顶满）所以必能表示。那么 \(w_n=g^{q_n}\)。以下 \(=\) 在模意义下进行

\(\omega_n^0,\omega_n^1,\omega_n^2,\cdots,\omega_n^{n-1}\) 互不相同：\(g^0,g^{q_n},g^{2q_n},\cdots,g^{(n-1)q_n}\) 确实互不相同。这是定义。
\(\omega_n^0=\omega_n^n=1\)：\(g^0=g^{nq_n}=g^{P-1}=1\)，费马小定理。
\(\omega_n^k=\omega_{2n}^{2k}\)：\(g^{kq_n}=g^{2kq_{2n}}\)，注意这里必然有 \(q_n=2q_{2n}\)（观察 \(q_n\) 定义），所以两边相等。
\(\omega_n^k=-\omega_n^{k+n/2}\)：对于 \(\omega_n^{k+n/2}=g^{kq_n}\cdot g^{n/2q_n}\) 的右边，其平方为 \({(g^{n/2q_n})}^2=g^{nq_n}=g^{P-1}=1\)，考虑到原根的定义：\(g^{n/2q_n}\neq g^{P-1}=1\)，故 \(g^{n/2q_n}=-1\)，故原式成立。

好的有了这些我们已经可以做 DFT，但是 IDFT 呢？我们在 IDFT 中用到的有：

\(\omega_n^n=1\) 显然。
\(\omega_n\) 的倒数：模意义下取个逆元。
\(\div n\)：逆元。

~~好的什么都不用变那我们 win 了~~

code：NTT