题解 LOJ535【「LibreOJ Round #6」花火】/ ZR22NOIP9A【逆序对】

posted on 2022-10-24 09:07:38 | under 题解 | source

problem

排列 \(a\)，可以进行至多一次操作：交换 \(a\) 中的任意两个数。求操作后最少的逆序对数。\(n\leq 10^6\)。

solution 0

相当于能去掉的最多的逆序对。

\[[*]=\max_{l,r}\{c(l,r,<a_{l-1})-c(l,r,>a_{l-1})+c(l,r,>a_r)-c(l,r,<a_r)\}. \]

solution 1

思考：交换操作到底是什么？

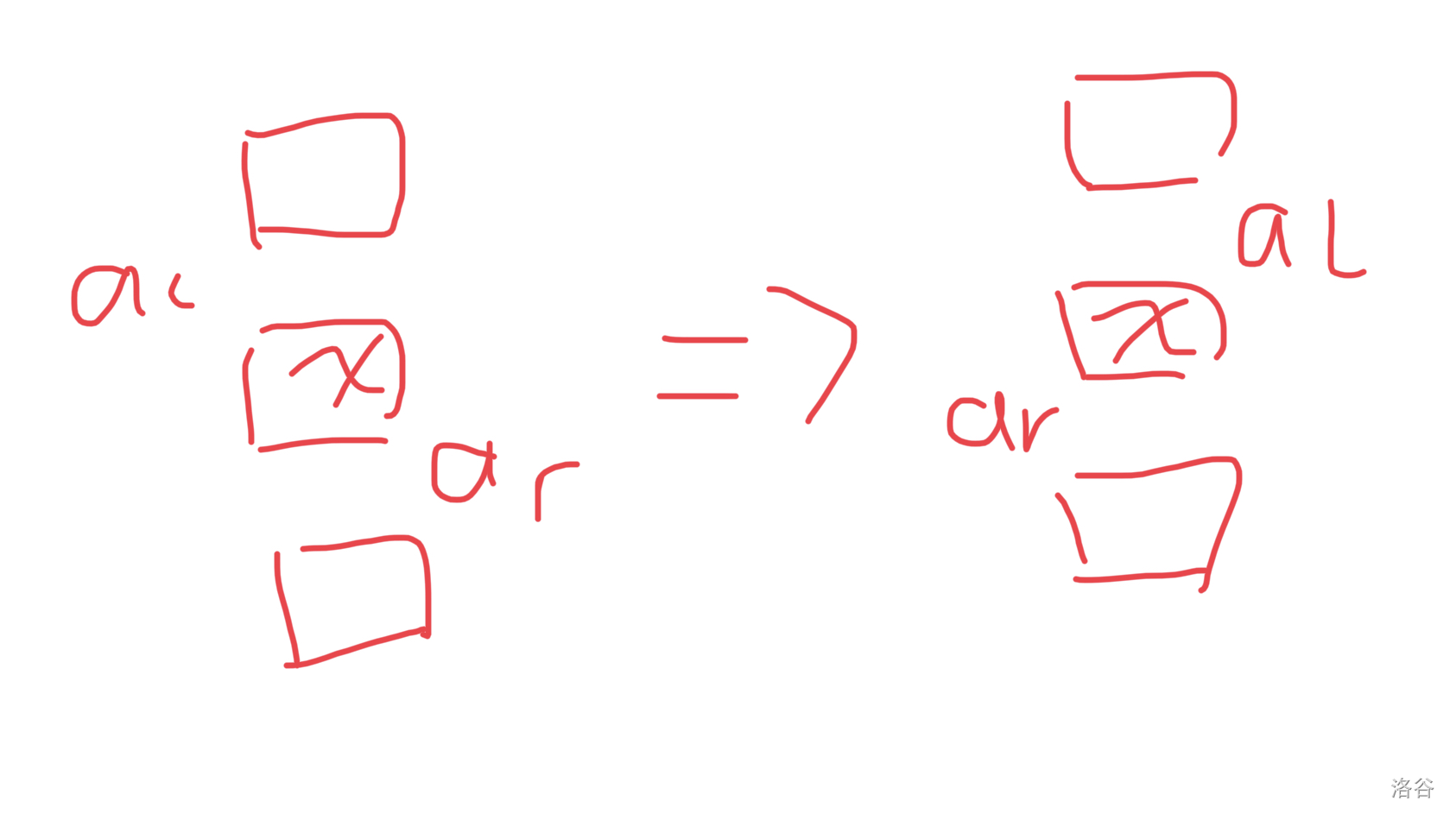
答案可以为 \(0\)！\(a_l<a_r\) 时答案为负数，弃之。画图理解:

\[[*]=2\times \max_{l,r,a_l>a_r}\{count(l,r,[a_r,a_l])\}-3. \]

（这是奇数！）

原题 \(\Rightarrow\) 平面上有形如 \((i,a_i)\) 的 \(n\) 个点，其中 \(a_i\) 是一个排列，求一个子矩阵满足：

• 左上角和右下角各有一个点；

最大化子矩阵内的点数。

对其暴力，\(O(n^2\log n)\)，不过比 solution 0 优越的多。

solution 2

如果一个点 \((x_1,y_1)\) 作为左上角，同时有一个 \((x_2,y_2),s.t.,x_2<x_1,y_2>y_1\) 那么 \((x_1,y_1)\) 是不是就寄了？

那么真正有效的左上角一定满足 \(x_1<x_2,y_1<y_2\)，右下角也是一样的。

接下来是惊人结论：随着左上角决策向上移，右下角的最优决策也随之上移！这就是决策单调性。

不能直接 \(O(n)\) 枚举（是假的呢）。考虑怎么用决策单调性。难道暴力吗？

solution 3.1

考虑这么一件事情：就是你已经有 \((x_1,y_1,x_2,y_2)\) 的答案，欲将扩展到 \((x_1,y_1,x_2{\color{red}+1},y_2)\)。这是 \(O(\log n)\) 的吗？

其实不然，观察到这是一个排列，在那个横坐标上就一个点，暴力就行。\(O(1)\)。

考虑像 CF868F 那样进行分治。当前分治左上角为 \([l,r]\)，右下角可用决策为 \([L,R]\)。试图计算 \(mid=\frac{l+r}{2}\) 的答案，直接扫一遍 \([L,R]\)，找一个最优的决策点 \(P\)，那么 \([l,mid-1]\) 用 \([L,P]\)，\([mid+1,r]\) 用 \([P,R]\) 就能尽可能的利用信息。

转移的时候用莫队那样的东西做。分析复杂度：每一层每个指针都均摊 \(O(n)\)，一共 \(O(n\log n)\) 的移动量。复杂度很对。

solution 3.2

考虑扫描线。

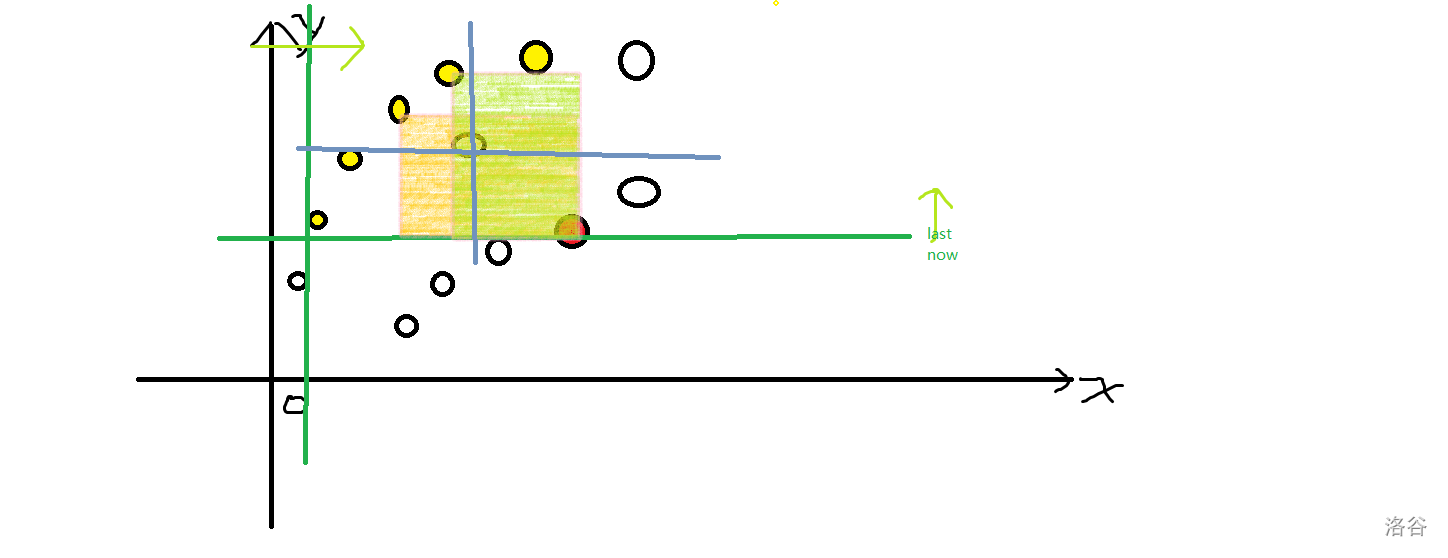
一个点对前缀最大值的贡献是一段区间；枚举右下角时可用决策具有单调性。

code 1

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int n,m,k,a[1000010],b[1000010],c[1000010],d[1000010];
struct ds{
	int lx,rx,ly,ry,ans;
	ds():lx(1),rx(0),ly(1),ry(0),ans(0){}
	void addline(int x,int ly,int ry){ans+=ly<=a[x]&&a[x]<=ry;}
	void delline(int x,int ly,int ry){ans-=ly<=a[x]&&a[x]<=ry;}
	void addrow(int y,int lx,int rx){ans+=lx<=d[y]&&d[y]<=rx;}
	void delrow(int y,int lx,int rx){ans-=lx<=d[y]&&d[y]<=rx;}
	int operator()(int Lx,int Rx,int Ly,int Ry){
		while(Lx<lx) addline(--lx,ly,ry);
		while(rx<Rx) addline(++rx,ly,ry);
		while(Ly<ly) addrow(--ly,lx,rx);
		while(ry<Ry) addrow(++ry,lx,rx);
		while(lx<Lx) delline(lx++,ly,ry);
		while(rx>Rx) delline(rx--,ly,ry);
		while(ly<Ly) delrow(ly++,lx,rx);
		while(Ry<ry) delrow(ry--,lx,rx);
		return ans;
	}
} ccf;
int solve(int l,int r,int L,int R){
	if(l>r) return -1e9;
	int mid=(l+r)>>1,p=L,pans=-1e9;
	for(int i=L;i<=R;i++){
		int res=ccf(b[mid],c[i],a[c[i]],a[b[mid]]);
//		printf("ccf(%d,%d,%d,%d)=%d\n",b[mid],c[i],a[c[i]],a[b[mid]],res);
		if(b[mid]<c[i]&&a[b[mid]]>a[c[i]]&&res>pans) pans=res,p=i;
	}
//	printf("solve(%d,%d,%d,%d)=%d\n",l,r,L,R,pans);
	return max({pans,solve(l,mid-1,L,p),solve(mid+1,r,p,R)});
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]),d[a[i]]=i;
	for(int i=1;i<=n;i++) if(!m||a[b[m]]<a[i]) b[++m]=i;
	for(int i=n;i>=1;i--) if(!k||a[c[k]]>a[i]) c[++k]=i;
	reverse(c+1,c+k+1);
	printf("%d\n",max(solve(1,m,1,k)*2-3,0));
	return 0;
}

code 2

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
template<int N> struct segtree{
	int ans[N<<2],tag[N<<2];
	segtree(){memset(ans,~0x3f,sizeof ans),memset(tag,0,sizeof tag);}
    //看，这里 ans 初值为 inf，贡献不能算到非决策点上，我们要 ban 掉
	void add(int p,int k){tag[p]+=k,ans[p]+=k;}
	void pushdown(int p){add(p<<1,tag[p]),add(p<<1|1,tag[p]),tag[p]=0;}
	void modify(int L,int R,int k,int p=1,int l=1,int r=N){
		if(L<=l&&r<=R) return add(p,k);
		int mid=(l+r)>>1; pushdown(p);
		if(L<=mid) modify(L,R,k,p<<1,l,mid);
		if(mid<R) modify(L,R,k,p<<1|1,mid+1,r);
		ans[p]=max(ans[p<<1],ans[p<<1|1]);
	}
	void cover(int x,int k,int p=1,int l=1,int r=N){
		if(l==r) return (void)(ans[p]=k,tag[p]=0);
		int mid=(l+r)>>1; pushdown(p);
		if(x<=mid) cover(x,k,p<<1,l,mid);
		else cover(x,k,p<<1|1,mid+1,r);
		ans[p]=max(ans[p<<1],ans[p<<1|1]);
	}
	int query(int L,int R,int p=1,int l=1,int r=N){
		if(L<=l&&r<=R) return ans[p];
		int mid=(l+r)>>1,res=-1e9; pushdown(p);
		if(L<=mid) res=max(res,query(L,R,p<<1,l,mid));
		if(mid<R) res=max(res,query(L,R,p<<1|1,mid+1,r));
		return res;
	}
};
int n,a[1000010],b[1000010],premax[1000010],sufmin[1000010];
segtree<1000010> t;
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]),b[a[i]]=i;
	premax[0]=-1e9;for(int i=1;i<=n;i++) premax[i]=max(premax[i-1],a[i]);
	sufmin[n+1]=1e9;for(int i=n;i>=1;i--) sufmin[i]=min(sufmin[i+1],a[i]);
	int last=1,now=1,ans=0;
	for(int i=1;i<=n;i++){
		if(premax[i]==a[i]) t.cover(i,0);//决策点可用，开启
		t.modify(lower_bound(premax+1,premax+i+1,a[i])-premax,i,1);
		if(sufmin[i]==a[i]){
			for(;last<=a[i];last++) t.modify(1,b[last],-1);
			for(;premax[now]<a[i];now++);
			if(now<=i) ans=max(ans,t.query(now,i));
		}
	}
	printf("%d\n",max(2*ans-1,0));
	return 0;
}