题解 QOJ1884【Mission Impossible: Grand Theft Auto】/ ZROI2610【[23ab-day3] 染色】

题解 ZROI2610【[23ab-day3] 染色】

problem

给定一棵树。初始是全黑的。

假设有 $m$ 个节点度数为 $1$，你可以进行 $\lfloor m/2\rfloor+1$ 次染色，每次染色过程会依次执行以下两步操作：

1. 选择两个节点 $a,b$，把 $a,b$ 简单路径上的所有点涂白。
2. 所有黑点扩散，也就是所有相邻点有黑点的白点同时变成黑色。

求出一组方案使得经过 $\lfloor m/2\rfloor+1$ 次染色之后树变成全白，或者判断无解。

对于 $100\%$ 的数据，$1\le T\le100,2\le n\le 2\times 10^5,\sum n\le 2\times 10^5$。

solution

大胆猜测有解。并发现我们染色的两端一定是叶子；还发现二度点可以完全删掉不管；除了一条链的情况，都可以选出一个三度点作为根。设有 \(m\) 片叶子，则这棵树缩链后最多只有 \(2m-2\) 个点（设共有 \(m+x\) 个点，\(x\) 个点至少三度，\(m+3x\leq 2(m+x-1)\implies m-x\geq2\implies m+x\leq 2m-2\)）。

考虑不顾操作次数限制怎么做，我们有一个做法是按照 dfn 序遍历叶子，记叶子的 dfn 序分别为 \((l_1,l_2,\cdots,l_m)\)，我们可以大胆输出 \((l_1,l_2),(l_1,l_3),(l_1,l_4)\cdots\) 不难发现这样一定合法。考虑优化之，如果我们找到一个 \(x\)，然后输出 \((l_x,l_{x+1}),(l_{x-1},l_{x+3}),(l_{x-2},l_{x+4}),\cdots\) 其中编号对 \(m\) 取模，但是这会有一个问题就是会有一条边没有被覆盖（称为坏边）。为什么呢？大概看看这个图：

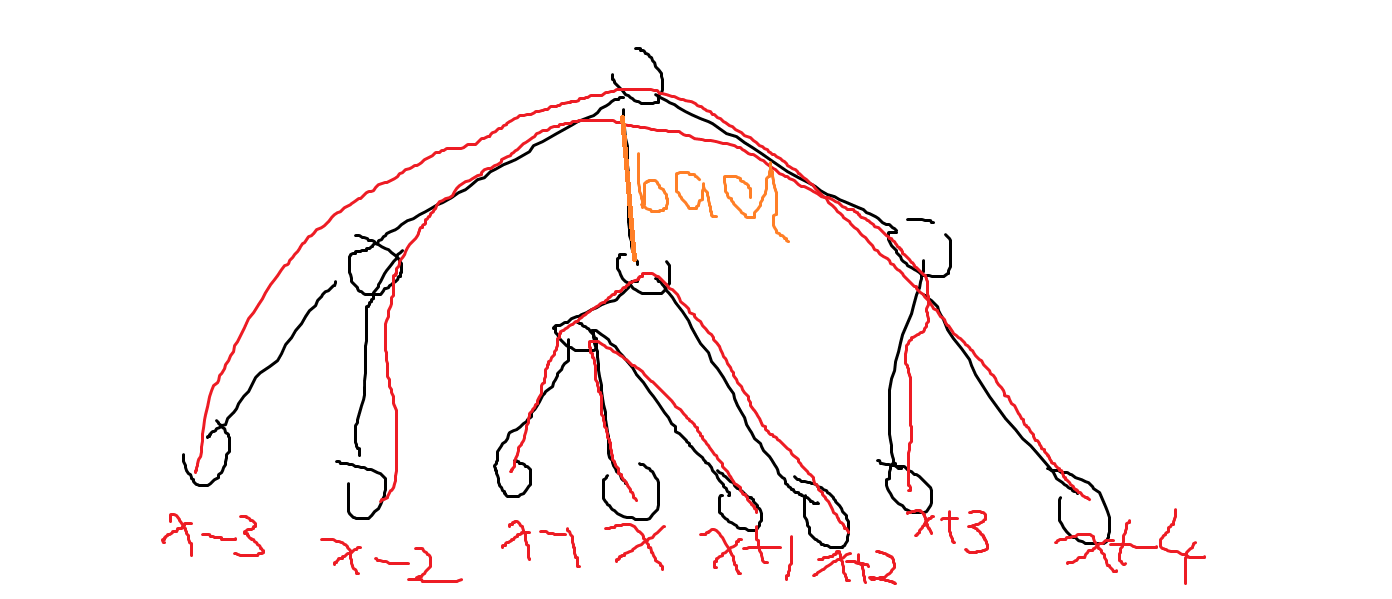
中间橙色的边没有被覆盖，称他是 bad 的。在 bad 边上的黑点，覆盖了 \((l_{x-1}, l_{x+2})\) 以后扩散到 bad 边下面的白点，然后覆盖 \((l_{x-2}, l_{x+3})\) 的时候没有覆盖到刚刚下去的黑点，于是就寄了。

考虑证明一个东西，就是合法方案中如果全是叶子作为端点，那么只有所有边都被覆盖，才是合法方案。否则，那条没有被覆盖的边两次被覆盖的时间不一样，会被染黑。证明可以看看上面的图，比较直观，主要是严谨证明不会。

考虑对于一条边，处理出哪些 \(x\) 会使得这条边没被染到（在子树内两两匹配，子树外也要讨论），然后选一条没有被限制的边，这样就行了。根据鸽巢原理（其实我不会证，但是拍过了），能找出这样的一条边。对于 \(m\) 为偶数的情况，可以在根上挂一片叶子，也能构造出来。

这东西太难写也很难证明，SPJ 更是神奇，就这样吧。。。

考虑到缩链后有最多 \(2m-2\) 个点，\(2m-3\) 条边，每条可能的 bad 边对应了至多一个叶子 \(x\)，使得以 \(x\) 为中心开始构造时这条边会成为 bad 边；因为 bad 边下面的子树内，根据有奇数个或者偶数个叶子，可能会被 \(x\) 认为是 bad 边的只会有至多一个。而因为共有 \(m\) 个叶子，根据鸽巢原理，存在一个叶子使得它有至多一条 bad 边。用这个叶子开始操作，直到覆盖到 bad 边下方的黑点时，多用一次操作覆盖掉 bad 边即可。

如果 \(m\) 是奇数，当所有操作都完成时或者要覆盖 bad 边时，把多的那个叶子和任意一个叶子（或者 bad 边下的叶子）覆盖掉；如果 \(m\) 是偶数，除了链，可以考虑在随机位置多挂一个叶子，反正没有区别。

code

#include <tuple>
#include <cstdio>
#include <vector>
#include <cstring>
#include <cassert>
#include <random>
#include <algorithm>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr,##__VA_ARGS__)
#else
#define debug(...) void(0)
#endif
typedef long long LL;
mt19937 rng{random_device{}()};
int n,cnt,L[1<<18],R[1<<18],fa[1<<18];
vector<tuple<int,int,int>> inv[1<<18];
vector<int> g[1<<18],lvs;
void dfs(int u,int f=0){
	L[u]=lvs.size(),fa[u]=f;
	if(g[u].size()==1) lvs.push_back(u);
	for(int v:g[u]) if(v!=f) dfs(v,u);
	R[u]=lvs.size();
}
int mian(){
	for(int i=1,u,v;i<n;i++) scanf("%d%d",&u,&v),g[u].push_back(v),g[v].push_back(u);
	puts("YES");
	int root=1,m=0,flag=0;
	for(int i=1;i<=n;i++) if(g[i].size()>2) root=i; else if(g[i].size()==1) m++;
	if(m==2){
		for(int i=1;i<=n;i++) if(g[i].size()==1) printf("%d ",i); puts("");
		for(int i=1;i<=n;i++) if(g[i].size()==1) printf("%d ",i); puts("");
		return 0;
	}
	if(m%2==0) g[++n].push_back(root),g[root].push_back(n),flag=1;
	dfs(root);
	m=lvs.size();
	for(int u=1;u<=n;u++){
		if(g[u].size()>2){
			if((R[u]-L[u])%2==0) inv[(L[u]+R[u]-1)>>1].emplace_back((R[u]-L[u])>>1,L[u],R[u]);
			else if(R[u]-L[u]!=m) inv[((R[u]+m+L[u]-1)>>1)%m].emplace_back((m-R[u]+L[u])>>1,L[u],R[u]); 
		}
	}
	int x=0;
	for(int i=0;i<m;i++) if(inv[i].size()<inv[x].size()) x=i;
	assert(inv[x].size()==0);
	debug("root=%d,x=%d\n",x,root);
	debug("lvs:"); for(int x:lvs) debug("%d ",x); debug("\n");
	int cnt=0;
	for(int i=1;i<=n;i++){
		debug("u=%d,L=%d,R=%d,fa=%d\n",i,L[i],R[i],fa[i]);
	}
	auto print=[&](int u,int v){
		u=(u%m+m)%m,v=(v%m+m)%m;
		if(u==v) v++,v%=m;
		u=lvs[u],v=lvs[v];
		auto chk=[&](int u){return flag&&u==n?root:u;};
		u=chk(u),v=chk(v);
		assert(u!=v),printf("%d %d\n",u,v);
	};
	auto y=inv[x].empty()?make_tuple(-1,-1,-1):inv[x][0];
	for(int i=0;i<m/2+1;i++){
		if(i==get<0>(y)) debug("upd"),print(get<1>(y),get<2>(y));
		print(x-i,x+1+i);
	}
	return 0;
}
void reset(){
	for(int i=1;i<=n+1;i++) g[i].clear(),inv[i].clear();
	lvs.clear();
}
int main(){
//	#ifdef LOCAL
//	 	freopen("input.in","r",stdin);
//	#endif
	for(scanf("%*d%*d");~scanf("%d",&n);reset(),mian());
	return 0;
}