题解 UVA12265【贩卖土地 Selling Land】

posted on 2022-09-24 14:33:29 | under 题解 | source

problem

一个黑白矩阵，求以每个点为右下角，能围出的周长最大的全白矩形的周长。\(n\leq 2000\)。

solution

试图进行线性 DP，令 \(f_{i,j}\) 表示以 \((i,j)\) 为右下角的答案。

尝试从 \(f_{i-1,j},f_{i,j-1}\) 转移到 \(f_{i,j}\)，但是以一个点为右下角的空矩阵有很多，不能全部存下来，怎么办呢？那就不要存了。

换一种思路，我们从一行的角度看它，举个例子：

从点 \((i,j)\) 一直往左走，底下那条边（称为宽）越长，能往上延伸出的长度（称为高）越矮。更形式化地说，令 \(g_{i,j}\) 为点 \((i,j)\) 往上有多少块空地，那我们可以枚举一个宽 \(len\)，对应的高就是 \(\min\limits_{i-len<j\leq i}\{g_{i,j}\}\)，那么点 \((i,r)\) 的答案就是：（变量含义有变化）

\[ans_{i,r}=\max_{l}\{\min_{l\leq j\leq r}\{g_{i,j}\}+r-l+1\} \]

从这里分出两种理解方式：

代数

将 \(r+1\) 丢出去：

\[ans_{i,r}=\max_{1\leq l\leq r}\{\min_{l\leq j\leq r}\{g_{i,j}\}-l\}+r+1 \]

我们令 \(las_{i,r}\) 为一个最大的 \(k\) 使得 \(g_{i,k}<g_{i,r}\)，把 \(l\) 的枚举范围 \([1,r]\) 分成两部分：

• \([las_{i,r}+1,r]\)：显然这一部分总是 \(g_{i,r}-l\)。
• \([1,las_{i,r}]\)：写出来就是 \(\max_{1\leq l\leq las_{i,r}}\{\min_{l\leq j\leq las_{i,r}}\{g_{i,j}\}-l\}\)，非常感动，这是 \(ans_{i,las_{i,r}}\) 求过的东西，于是直接拿过来用。

已经做完了。

几何

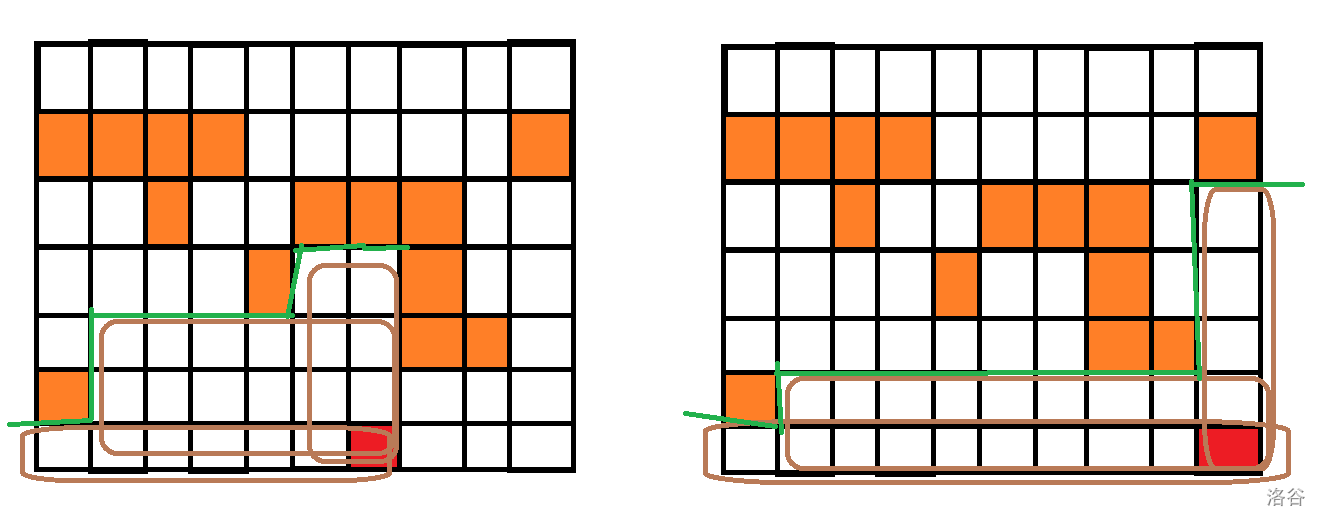
（求以红色方块为右下角的答案，橙色不能踩）

可以把那条绿线看成一种类似轮廓线的东西，我们只需要维护轮廓线底下这些棕色矩形就可以了。容易发现轮廓线是单调不降的，因此我们可以用一个单调栈维护这条线的折角处，顺带维护栈中的最大值（连着折角一起放入栈，一起弹出栈）就可以了。

code

//lock /kk
#include <cstdio>
#include <cstring>
#include <utility>
#include <algorithm>
using namespace std;
int n,m;
char a[5010][5010];
int us[5010][5010],ret[100010];
int stk[5010],mx[5010];
void dp(){
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(a[i][j]=='.'){
				us[i][j]=us[i-1][j]+1;
			}
		}
	}
	int top=0;
	mx[0]=-1e9;
	for(int i=1;i<=n;i++){
		stk[top=0]=0;
		for(int j=1;j<=m;j++){
			if(a[i][j]=='#') stk[top=0]=j;
			else{
				while(top&&us[i][stk[top]]>=us[i][j]) top--;
				stk[++top]=j;
				mx[top]=max(mx[top-1],us[i][j]-stk[top-1]);
				ret[mx[top]+j]++;
			}
		}
	}
}
int mian(){
//	freopen("run.in","r",stdin);
//	freopen("run.out","w",stdout);
	memset(us,0,sizeof us);
	memset(ret,0,sizeof ret);
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%s",a[i]+1);
	dp();
	for(int i=1;i<=n+m;i++){
		if(ret[i]) printf("%d x %d\n",ret[i],i*2);
	}
	return 0;
}
int main(){
	for(scanf("%*d");~scanf("%d%d",&n,&m);mian());
	return 0;
}