题解 LGP8820【[CSP-S 2022] 数据传输】

posted on 2022-10-30 16:27:18 | under 题解 | source

problem

一棵 \(n\) 个点的树。如果两个点在树上的距离不超过 \(k\)，我们称这两个点可以互相传送信息。现在 \(q\) 次给定 \(s,t\)，选出 \(h=\{h_1=s,h_2,h_3,\cdots,h_{c-1},h_c=t\}\) 这 \(c\) 个点，满足相邻两个点可以互相传送信息，请最小化 \(\sum_{i\in h}v_i\)。

前置知识

\(\{\max,+\}\) 矩阵乘法 / 动态 DP。对于矩阵 \(a,b,c\)，这是我们所熟知的矩阵乘法 \(c=a\times b\)：

\[c=a\times b\Rightarrow c_{i,j}=\sum_{k}a_{i,k}b_{k,j}. \]

现在我们定义矩阵 \(*\) 法：

\[c=a*b\Rightarrow c_{i,j}=\min_{k}\{a_{i,k}+b_{k,j}\}. \]

为了更好地理解矩阵 \(*\) 法，您可以认为，\(c_{i,j}\) 的值是 \(a\) 的第 \(i\) 行顺时针旋转 \(90^\circ\) 后与 \(b\) 的第 \(j\) 列依次相加取最小值的结果。如果某一个值是 \(\infty\) 代表强制不选，如果是 \(0\) 代表继承。

我们可以证明，矩阵 \(*\) 法没有交换律，但有结合律。

solution when \(k\leq 2\)

\(k=1\) 是【模板】链上求和。将 \(s\to t\) 这条链拉出来，记链上第 \(i\) 个点的答案为 \(f_i\)，我们不妨把 \(f_i\) 写成矩阵 \(*\) 法之形式。

\[\begin{bmatrix}f_{i-1}\end{bmatrix}*\begin{bmatrix}v_{h_i}\end{bmatrix}=\begin{bmatrix}f_i\end{bmatrix}. \]

\(k=2\) 时一定会在链上走，如果走下去了回不去，答案更劣。

\[\begin{bmatrix}f_{i-1},f_{i-2}\end{bmatrix} *\begin{bmatrix} v_{h_i},&0\\ v_{h_i},&\infty\\ \end{bmatrix} =\begin{bmatrix}f_{i},f_{i-1}\end{bmatrix}.\]

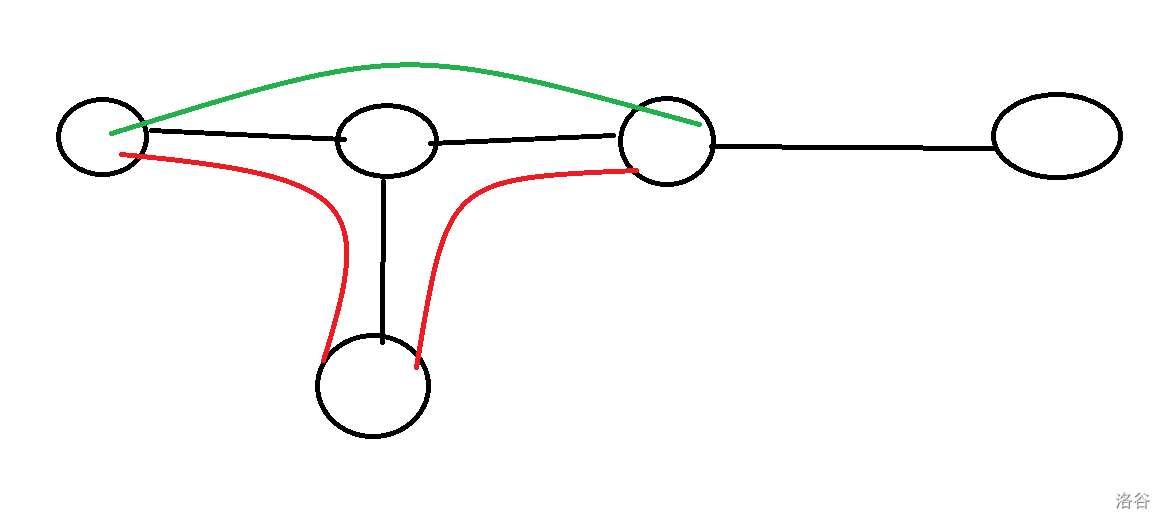
（走下去再返回（即红边）不如不走（即绿边））

solution when \(k=3\)

\(k=3\) 时最多向下走一步，不然就走不出去了。令 \(f_{i,0}\) 表示在点 \(i\) 的最小代价，\(f_{i,1}\) 表示在 \(i\) 的某一个儿子（可以算上父亲，这不重要）上的最小代价。

\[\begin{cases} b_i&=\min_{\text{j是i的儿子或父亲}} v_j.\\ f_{i,0}&=\min\{f_{i-3,0},f_{i-2,0},f_{i-2,1},f_{i-1,0},f_{i-1,1}\}+v_{h_i}.\\ f_{i,1}&=\min\{f_{i-2,0},f_{i-1,0},f_{i-1,1}\}+b_{h_i}.\\ \end{cases}\]

考虑优化：我们不太关心这些点在链上还是不在链上。令 \(f_{i,j}\) 表示现在在离第 \(i\) 个点距离为 \(j\) 的点上。重定义 \(b_i=\min_{\text{j是i的儿子}} v_j\)。

\[\begin{bmatrix}f_{i-1,0},f_{i-1,1},f_{i-1,2}\end{bmatrix} *\begin{bmatrix} v_{h_i},&0,&\infty\\ v_{h_i},&b_{h_i},&0\\ v_{h_i},&\infty,&\infty\\ \end{bmatrix} =\begin{bmatrix}f_{i,0},f_{i,1},f_{i,2}\end{bmatrix} \]

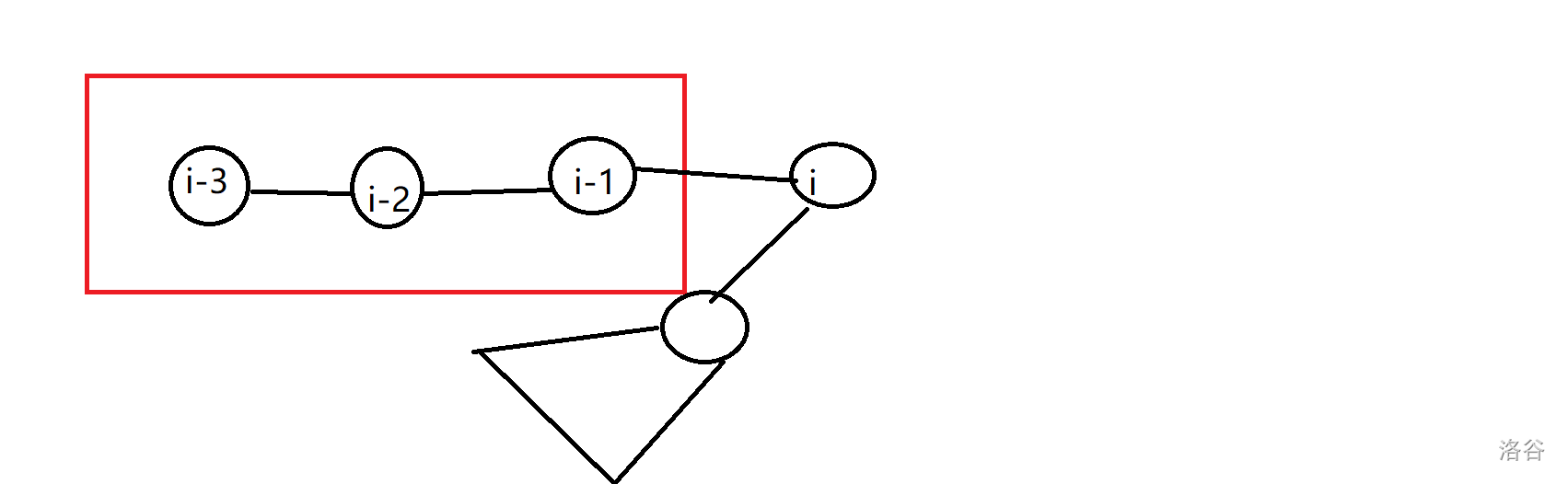
（这里转移不用关心走到 \(i-1\) 的情况，已经在 \(f_{i-1,0}\) 那里算过了，不用管）

（这里 \(b_i\) 仅限儿子，在 LCA 处要稍微动一下，加上父亲的贡献）

（为了不分讨，可以强行认为 \(f_0=\begin{bmatrix}\infty,\infty,0\end{bmatrix}\)，尽管它并没有实际意义）

于是你会了暴力。

solution 的优化

考虑把这玩意多组询问。

观察到每一个转移矩阵只和 \(h_i,v_{h_i},b_{h_i}\) 有关，而后两个可以预处理，那么转移矩阵可以预处理。

模仿倍增 LCA，我们也整一个 \(dw_{i,j},up_{i,j}\)，分别表示以 \(i\) 为最后一个点，从上往下 / 从下往上数 \(2^j\) 个父亲的矩阵 \(*\) 和。转移可以从 \(2^{j-1}\) 那里拼起来，\(O(nk^3\log n)\)；询问可以把路径拆成 \(s\to lca(s,t),lca(s,t),lca(s,t)\to t\) 三段，分别 \(O(k^3\log n)\) 的求出矩阵 \(*\) 和，求出答案即可。

总的复杂度为 \(O((n+q)k^3\log n)\)。

code

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef long long LL;
template<int N,int M,class T=LL> struct matrix{
	T a[N][M];
	matrix(T flag=1e18){memset(a,0x3f,sizeof a);for(int i=0;i<N&&i<M;i++) a[i][i]=flag;}
	T* operator[](int i){return a[i];}
};
template<int N,int M,int R,class T=LL> matrix<N,R,T> operator*(matrix<N,M,T> a,matrix<M,R,T> b){
	matrix<N,R,T> c=1e18;
	for(int i=0;i<N;i++){
		for(int j=0;j<M;j++){
			for(int k=0;k<R;k++){
				c[i][k]=min(c[i][k],a[i][j]+b[j][k]);
			}
		}
	}
	return c;
};
template<int N,int M,class T=int> struct graph{
	int head[N+10],nxt[M*2+10],cnt;
	struct edge{
		int u,v; T w;
		edge(int u=0,int v=0,T w=0):u(u),v(v),w(w){}
	} e[M*2+10];
	graph(){memset(head,cnt=0,sizeof head);}
	edge& operator[](int i){return e[i];}
	void add(int u,int v,T w=0){e[++cnt]=edge(u,v,w),nxt[cnt]=head[u],head[u]=cnt;}
	void link(int u,int v,T w=0){add(u,v,w),add(v,u,w);}
};
LL a[200010],b[200010];
int n,m,sshwy,fa[19][200010],dep[200010];
graph<200010,200010> g;
matrix<3,3> dw[19][200010],up[19][200010];
matrix<1,3> f0;
matrix<3,3> gettrans(int i,LL del=1e18){
	matrix<3,3> c=1e18; 
	switch(sshwy){
		case 1: c[0][0]=a[i]; break;
		case 2: c[0][1]=0,c[0][0]=c[1][0]=a[i]; break;
		case 3: c[0][0]=c[1][0]=c[2][0]=a[i],c[0][1]=c[1][2]=0,c[1][1]=min(b[i],del); break;
	}
	return c;
}
void dfs(int u,int f=0){
	dep[u]=dep[fa[0][u]=f]+1,b[u]=1e18;
	for(int i=g.head[u];i;i=g.nxt[i]){
		int v=g[i].v; if(v==f) continue;
		dfs(v,u),b[u]=min(b[u],a[v]);
	}
	dw[0][u]=up[0][u]=gettrans(u);
}
int lca(int u,int v){
	if(dep[u]<dep[v]) swap(u,v); int d=dep[u]-dep[v];
	for(int j=18;j>=0;j--) if(d>>j&1) u=fa[j][u];
	if(u==v) return u;
	for(int j=18;j>=0;j--) if(fa[j][u]!=fa[j][v]) u=fa[j][u],v=fa[j][v];
	return fa[0][u];
}
matrix<3,3> query_dw(int u,int k){
	matrix<3,3> res=0;
	for(int j=18;j>=0;j--) if(k>>j&1) res=dw[j][u]*res,u=fa[j][u];
	return res;
}
matrix<3,3> query_up(int u,int k){
	matrix<3,3> res=0;
	for(int j=18;j>=0;j--) if(k>>j&1) res=res*up[j][u],u=fa[j][u];
	return res;
}
LL query(int u,int v){
	int k=lca(u,v);
	matrix<1,3> res=f0*query_up(u,dep[u]-dep[k])*gettrans(k,a[fa[0][k]])*query_dw(v,dep[v]-dep[k]) 
	return min({res[0][0]-a[v],res[0][1],res[0][2]})+a[v];
}
int main(){
	scanf("%d%d%d",&n,&m,&sshwy);
	f0[0][sshwy-1]=0,a[0]=1e18;
	for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
	for(int i=1,u,v;i<n;i++) scanf("%d%d",&u,&v),g.link(u,v);
	dfs(1);
	for(int j=1;j<=18;j++){
		for(int i=1;i<=n;i++) fa[j][i]=fa[j-1][fa[j-1][i]];
		for(int i=1;i<=n;i++) dw[j][i]=dw[j-1][fa[j-1][i]]*dw[j-1][i];
		for(int i=1;i<=n;i++) up[j][i]=up[j-1][i]*up[j-1][fa[j-1][i]];
	}
	for(int u,v;m--;) scanf("%d%d",&u,&v),printf("%lld\n",query(u,v));
	return 0;
}