题解 LGP6619【[省选联考 2020 A/B 卷] 冰火战士】

posted on 2022-07-22 22:00:06 | under 题解 | source

无脑选手爬过来补题。

我们发现：无论冰火战士以什么样的顺序出场，都有以下性质：

• “能量守恒”：令 \(t\) 为场地温度，那么能上场的战士是固定的，它们有的能量是固定的。
• 两个战士的能量会同时减去一个常量。
• 最后的状态是，有一边战士的能量为 \(0\)，另一边有或者没有能量。

令 \(t\) 为场地温度，\((x,y)\in A\) 是冰战士的温度和能量，\((x,y)\in B\) 是火战士，我们可以把原问题抽象成：求最大的 \(x\) 使下式最大：

\[2\times \min\left\{\sum\limits_{(x,y)\in A}[x\leq t]y,\sum\limits_{(x,y)\in B}[x\geq t]y\right\} \]

因为 \(y\) 为正整数，那么随着 \(t\) 的增加，\(\sum\limits_{(x,y)\in A}[x\leq t]y\) 显然单调不降，\(\sum\limits_{(x,y)\in A}[x\geq t]y\) 显然单调不升。

怎么求这两东西？它本质上是一段前/后缀求和，考虑开两个树状数组，离散化 \(x\) 后把 \(x\) 当作下标，把 \(\pm1\) 当作值，这玩意是很容易写的。但注意，为了方便，维护后缀的树状数组插入时把 \(x\gets x+1\)，求后缀时直接写 \([1,2\times 10^6]-[1,x]\)，正确性显然。

我们来求答案，把这两个东西当作两个曲线画出来：

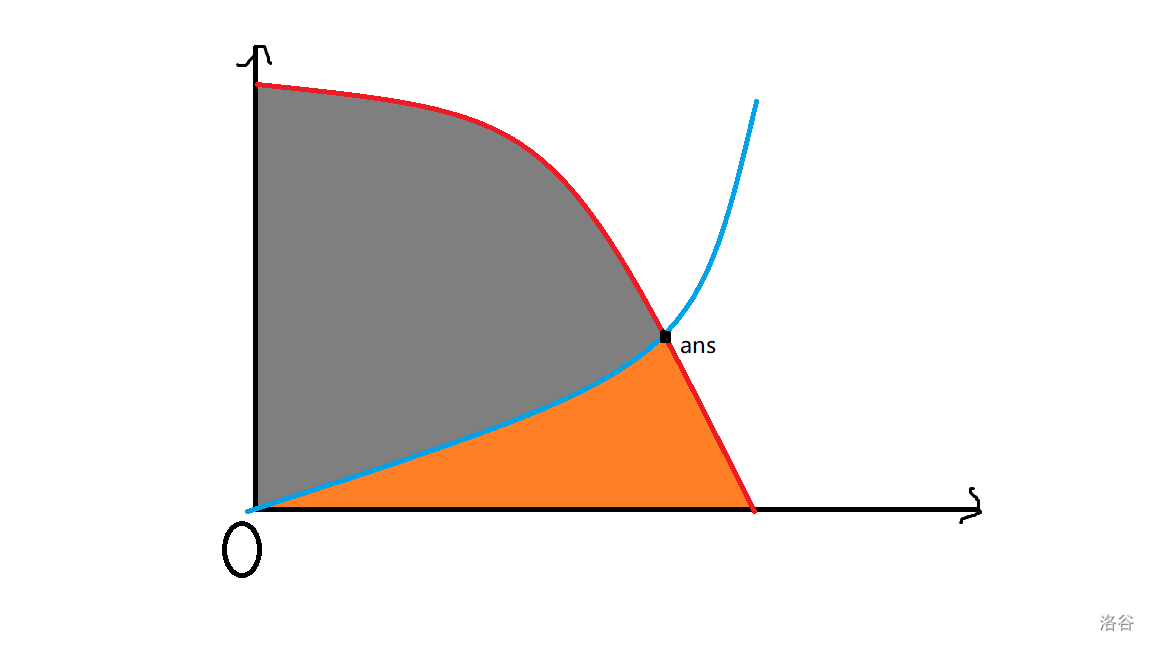
蓝色是冰战士，红色是火战士，它们的交点是答案。考虑求这个东西？三分不行，存在连续段；想到在 \(ans\) 的左边，红线减去蓝线，这东西单调不升，我们可以尝试使用 \(\tt binary\_search\)，\(O(n\log^2 n)\)。

但有一个问题，\(t\) 是离散的（不连续），两条线是离散的，我们要的交点可能不存在。也没事，我们记 \(\tt binary\_search\) 的答案为 \(t_1\)，\(t_1\) 在 \(ans\) 的左边且离 \(ans\)（左边）最近，那 \(t_2=t_1+1\) 在 \(ans\) 的右边（反证法），\(t_2\) 也是一个解。如果 \(t_2\geq t_1\)，\(t_1\) 可以不要，但题目说要温度最高，因此我们再 \(\tt binary\_search\)，找另一个 \(t_3\) 在 \(ans\) 右边且最高，这样 \(t_1,t_3\) 取一个解，这道题就做完了。

你拿着 \(O(n\log^2 n)\) 的 \(\tt binary\_search\) 交题，TLE 60pts，我们来学习科技：树状数组二分。它更应该叫做倍增，具体的，开始时我们有一个 \(p=0\)，枚举 \(j=20\to 1\)：

• 令 \(q=p+2^j\)，显然 \({\tt lowbit}(q)=2^j\)，\(j\) 是从大到小枚举的。
• 那么，\(q\) 在树状数组上维护的值域是 \([p+1,q]\)（定义）。
• 如果加上 \(q\) 的答案仍合法，把它加上；否则忽略它。

像倍增 LCA 一样，我们不断逼近答案，重复利用已有信息，单次询问的复杂度变成了 \(O(\log n)\)，我们可以过掉这道题了。

话说什么时候无解呢？如果你算出的答案是 \(0\)，可以钦定它无解，根本没有战士上场。

#include <cstdio>
#include <cassert>
#include <cstring>
#include <utility>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef pair<int,int> node;
template<int N,class T=int> struct flower{
    T b[N+10];int cnt;
    flower():cnt(0){}
    T operator+=(T x){return b[++cnt]=x;}
    void work(){sort(b+1,b+cnt+1),cnt=unique(b+1,b+cnt+1)-b-1;}
    int operator()(T x){return lower_bound(b+1,b+cnt+1,x)-b;}
    T operator[](int x){return b[x];}
};
template<int N,class T=int> struct fenwick{
    T c[N+10];
    fenwick(){memset(c,0,sizeof c);}
    void add(T k,int p){for(;p<=N;p+=p&-p) c[p]+=k;}
    T query(int p,T ans=0){for(;p>=1;p-=p&-p) ans+=c[p];return ans;}
    T operator[](int x){return c[x];}
};
int n,q[2000010][3];
flower<2000010> b;
fenwick<1<<21> t1,t2;
int brute(int t){return min(t1.query(t),t2.query(2e6)-t2.query(t));}//求值
node solve(){
    int p=0,s1=0,s2=t2.query(2e6);//动态维护红蓝线
    for(int j=20;j>=0;j--){
    	int q=p+(1<<j);
    	if(s1+t1[q]<s2-t2[q]) s1+=t1[q],s2-=t2[q],p=q;
        //如果算上 q 仍在左边，跳过去
	}
    return node(min(s1,s2),p);
}
node bestccf(int f){//要找到 brute(p)=f 的最大的 p
	if(f>2e6) return node(0,0);
	int p=0,s1=0,s2=t2.query(2e6);
    for(int j=20;j>=0;j--){
    	int q=p+(1<<j);
    	if(s1+t1[q]<s2-t2[q]) s1+=t1[q],s2-=t2[q],p=q;
    	else if(min(s1+t1[q],s2-t2[q])==f) s1+=t1[q],s2-=t2[q],p=q;
        //我们踩到了右边，如果踩到了我们想要的点，也跳过去
	}
    return node(min(s1,s2),p);
} 
int main(){
//    #ifdef LOCAL
//    	freopen("input.in","r",stdin);
//    #endif
    scanf("%d",&n);
    for(int i=1,op,x;i<=n;i++){
        scanf("%d",&op);
        // q[i]={t,x,y};
        if(op==1) scanf("%d%d%d",&q[i][0],&q[i][1],&q[i][2]);
        else scanf("%d",&x),q[i][0]=q[x][0],q[i][1]=q[x][1],q[i][2]=-q[x][2];
        b+=q[i][1];
    }
    b.work();
    for(int i=1;i<=n;i++){
        (!q[i][0]?t1:t2).add(q[i][2],b(q[i][1])+q[i][0]);
        node res1=solve(),res2=bestccf(brute(res1.second+1)),res=max(res1,res2);
        //assert(brute(res1.second)==res1.first);
        //assert(brute(res2.second)==res2.first);
        printf(res.first?"%d %d\n":"Peace\n",b[res.second],2*res.first);
    }
    return 0;
}