题解 LGP5369【[PKUSC2018]最大前缀和】

最大前缀和，如果单纯要求这个东西，有两种做法：

1. 从前往后求，维护当前前缀和和最大前缀和。
2. 从后往前扫，维护最大前缀和 \(mx\)，在前面插入一个数时，\(mx:=\max(mx+a_i,0)\)。

problem

长为 \(n\) 的序列 \(a\)，求 \(\sum_{p}\max_i s_i\)，其中 \(p\) 为长为 \(n\) 的排列，\(s_i=s_{i-1}+a_{p_i}\)。\(n\leq 20\)。

solution

看到 \(n\leq 20\) 考虑状压。

考虑如果有了一个 \(p\)，我们画一下 \(s_i\) 的图像：

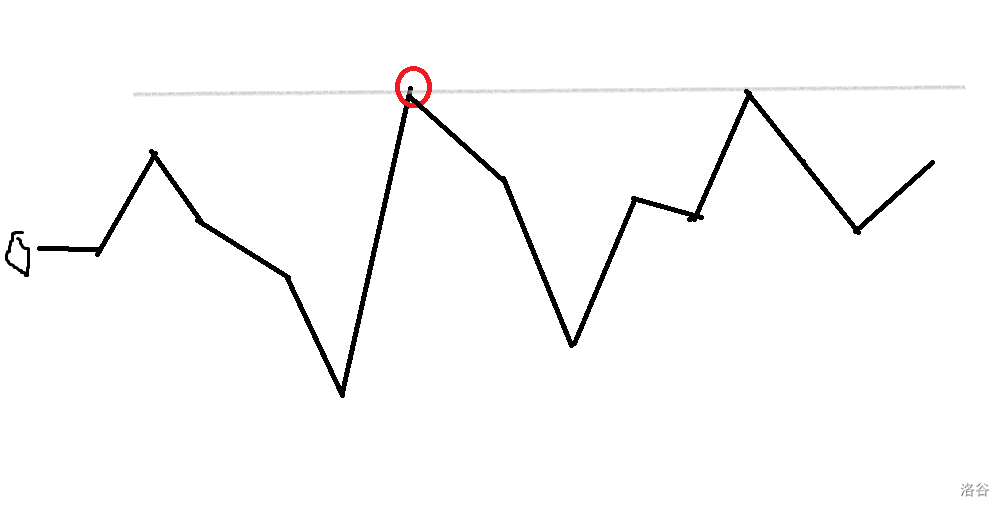
性质：

• 这是个折线图（
• 假如最高峰为 \(d\)，\(d\) 之前的所有线不能 碰到 \(d\)，之后的所有线不能 超过 \(d\)。

按照 \(d\) 的位置将图像分为前和后，假如前面一段的数的集合为 \(S\)，我们分别算出前一半的方案数 \(g_S\) 和后一半的方案数 \(f_{U\backslash S}\)，乘起来再乘上 \(S\) 中数的总和，就是答案了 /cy

以下令 \(sum_S=\sum_{x\in S}x\)。

how to solve \(f_S\)?

\(f_S\) 比较简单，我们重新定义一下基准值 \(0\) 为 \(d\)，那么就是说我们的 \(S\) 的任何一个前缀和不能超过 \(0\)（否则就超过 \(d\) 了，\(d\) 不是最大前缀和）。

考虑枚举一个新的元素进行转移：\(\forall S(sum_S\leq 0),\forall x\in S(sum_{S\cup\{x\}}\leq 0), f_S\to f_{S\cup\{x\}}\)。

how to solve \(g_S\)?

我们将这个折线图倒着写：从第一个 \(d\) 开始，我们倒着做减法，就是顺序反过来而且符号反过来，就是所有的后缀和的相反数小于 \(0\)，也就是所有后缀和大于 \(0\)。

考虑枚举一个新的元素，倒着加入 \(S\)：\(\forall S(sum_S>0),\forall x\in S(sum_{S\cup\{x\}}>0), g_S\to g_{S\cup\{x\}}\)。

但是有个问题：

1
-1

输出 \(-1\)，但是我们输出 \(0\)（

怎么办呢，问题在于真正的 \(0\) 点是不能算作答案的，但是我们强制把它算进去了。

我们另开一个 \(h\) 存储这种答案：\(\forall S(sum_S>0),\forall x\in S(sum_{S\cup\{x\}}\leq 0), g_S\to h_{S\cup\{x\}}\)。

这个转移只会出现一次，因此是正确的。计算答案的时候把 \(g,h\) 叠起来就行。

code

点击查看代码

#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr,##__VA_ARGS__)
#else
#define debug(...) void(0)
#endif
typedef long long LL;
const int P=998244353;
int lowbit(int x){return x&-x;}
void red(LL&x){x=(x%P+P)%P;}
int n;
LL f[1<<20],g[1<<20],sum[1<<20],h[1<<20];
LL dp(){
	f[0]=1;
	for(int i=0;i<n;i++) g[1<<i]=1;
	for(int S=0;S<1<<n;S++){
//		debug("g[%d]=%lld\n",S,g[S]);
		for(int j=0;j<n;j++){
			if(S>>j&1) continue;
			if(sum[S]<=0&&sum[S|1<<j]<=0) red(f[S|1<<j]+=f[S]);
			if(sum[S]>0&&sum[S|1<<j]>0) red(g[S|1<<j]+=g[S]);
			if(sum[S]>0&&sum[S|1<<j]<=0) red(h[S|1<<j]+=g[S]);
		}
	}
	LL ans=0,U=(1<<n)-1;
	for(int S=1;S<1<<n;S++){
		red(sum[S]);
		red(ans+=f[U^S]*(g[S]+h[S])%P*sum[S]);
//		debug("ans+=f[%d]*g[%d]*sum[%d], which is %lld*%lld*%lld\n",U^S,S,S,f[U^S],g[S],sum[S]);
	}
	return ans;
}
int main(){
//	#ifdef LOCAL
//	 	freopen("input.in","r",stdin);
//	#endif
	scanf("%d",&n);
	for(int i=0;i<n;i++) scanf("%lld",&sum[1<<i]);
	sum[0]=0;
	for(int i=1;i<1<<n;i++) sum[i]=sum[i^lowbit(i)]+sum[lowbit(i)];
	printf("%lld\n",dp());
	return 0;
}