题解 P5188 【[COCI2009-2010#4] PALACINKE】
posted on 2022-07-25 20:12:26 | under 题解 | source
做法:矩阵优化 DP + 容斥原理。
矩阵优化 DP
先不要考虑商品,写个不管约束条件的 DP。令 \(f_{t,u}\) 表示在 \(t\) 时刻安娜在结点 \(u\) 上的方案数。初始时有 \(f_{0,1}=1,f_{0,u\neq 1}=0\)。考虑转移,如果存在一条单向边 \((u,v)\),则我们能用 1 分钟(不买东西)或者 2 分钟(买东西)经过它,则
这就是朴素的 DP。发现奇妙的 \(N\leq 25,T\leq 10^9\),套路地想到矩阵乘法。这里的 DP 需要用到 \(t-1\) 和 \(t-2\) 两个时刻,因此矩阵至少要存下前两个时刻的 DP 值。题目要求至少 \(t\) 分钟内回到 \(1\) 的答案,因此我们还需要一个 \(ans\) 记录。我们可以构造这样的矩阵:
表示 \(t\) 时刻的 DP 值,我们希望找到一个方阵 \(X\) 使 \(I_tX=I_{t+1}\)。
首先把 \(I_{t,1,n+1\sim2n}\) 的值转移到 \(I_{t+1,1,1\sim n}\),这部分值不变都是 \(f_t\),在 \(X\) 的"左下角"填一排对角线 \(1\)。
然后我们要推 \(f_{t+1}\) 的 DP 值,它依赖于 \(f_t,f_{t-1}\)(务必区分 \(f_t,f_{t-1}\) 转移的含义,\(f_t\) 是直接经过商店不买东西,\(f_{t-1}\) 是进入商店买东西),如果存在一条边 \((u,v)\in E\),就将 \(X_{u,v+n},X_{u+n,v+n}\) 的值加一,使它转移。给一个具体的例子,感性理解一下:
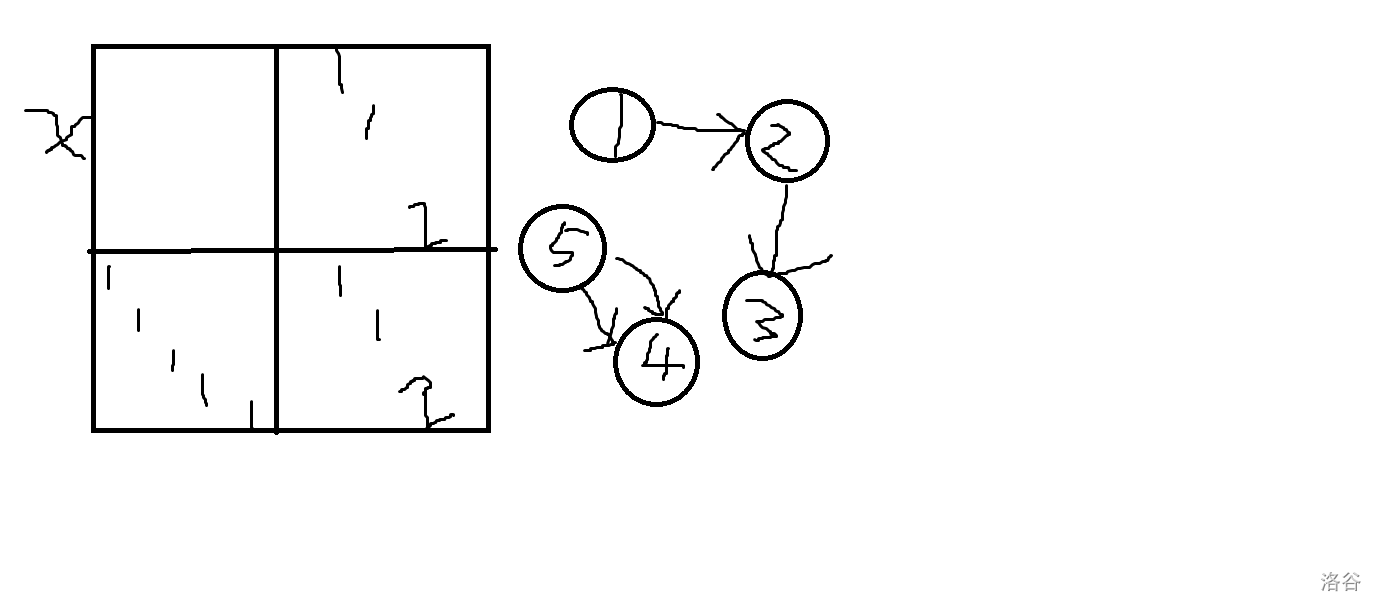
(关于如何想出这一个矩阵,个人理解是把矩阵乘法结果中第 \(i\) 行第 \(j\) 列看作是,\(a\) 矩阵的第 \(i\) 行顺时针旋转 \(90^\circ\),与 \(b\) 矩阵的第 \(j\) 列,重合在一起,算乘法的和。这样的方式可能能帮助你理解。)
还有一个 \(ans\),我们在最右下角 \(X_{2n+1,2n+1}\) 放一个 \(1\)(可以理解为继承上一次),再在 \(X_{n+1,2n+1}\) 放一个 \(1\)(可以理解为加上 \(f_{t,1}\) 的方案数)。于是我们有了 \(I_tX=I_{t+1}\),快速幂优化 \(I_1X^t=I_{t+1}\) 的转移即可。
容斥原理
回归题目,它要我们求出四种商品全买的方案数。直接求不好做,考虑合法方案数 + 不合法方案数 = 总方案数,总方案数显然是安娜在图上随便走的方案数,所以第一步把题意转化成不合法方案数。
令 \(B,J,M,P\) 分别为强制不买 B,J,M,P 的方案数,不合法的方案数就是 \(|B\cup J\cup M\cup P|\),发现这是个容斥原理,那么有
由于这是 \(\cap\)(交),把它理解成 \(\land\)(并),我们对于这当中的每个集合,强制不买那些商品(但是可以经过有那些商品的店而不进去买),按照上文的矩阵优化递推出合法方案数,最后就能得到我们想要的不合法的方案数。
实现
- 判断二进制数 \(t,s\) 在子集意义下是否有 \(t\subseteq s\),可以用
(~s&t)==0实现。 - 构造 \(I_1\) 矩阵时暴力计算 \(f_{1,u}\) 的方案数。
- 观察到这题模数很小,那么矩阵可以开
int,算完一个值统一取模,以减少常数(需要跑 \(16\) 次矩阵快速幂)。 - 务必搞清楚容斥系数!
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
int popcount(int x){return (x&1)+(x>>1&1)+(x>>2&1)+(x>>3&1);}
const int P=5557;
template<int N,int M,class T=int> struct graph{
int head[N+10],nxt[M*2+10],cnt;
struct edge{
int u,v;T w;
edge(int u=0,int v=0,T w=0):u(u),v(v),w(w){}
} e[M*2+10];
graph(){memset(head,cnt=0,sizeof head);}
edge operator[](int i){return e[i];}
void add(int u,int v,T w=0){e[++cnt]=edge(u,v,w),nxt[cnt]=head[u],head[u]=cnt;}
void link(int u,int v,T w=0){add(u,v,w),add(v,u,w);}
};
template<int N,int M,class T=LL> struct matrix{
T a[N+3][M+3];
matrix(bool f=0){
memset(a,0,sizeof a);
if(f) for(int i=1;i<=N;i++) a[i][i]=1;
}
T* operator[](int i){return a[i];}
void print(int n,int m){
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
printf("%d%c",a[i][j]," \n"[j==m]);
}
}
}
};
template<int N,int M,int R,class T=LL> matrix<N,R,T> operator*(matrix<N,M,T> a,matrix<M,R,T> b){
matrix<N,R,T> c=0;
for(int i=1;i<=N;i++){
for(int j=1;j<=R;j++){
for(int k=1;k<=M;k++){
c[i][j]+=a[i][k]*b[k][j];
}
c[i][j]%=P;
}
}
return c;
}
template<int N,class T=LL> matrix<N,N,T> operator^(matrix<N,N,T> a,LL b){
matrix<N,N,T> ans=1;
for(;b;b>>=1,a=a*a) if(b&1) ans=ans*a;
return ans;
}
int n,m,t,tb[128];
char buf[110];
graph<30,510,int> g;
matrix<60,60,int> o;
matrix<1,60,int> e;
int has(char *s){int res=0;for(int i=1,len=strlen(s+1);i<=len;i++) res+=tb[s[i]];return res;}
void binprt(int x){for(int i=3;i>=0;i--) putchar((x>>i&1)+'0');}
int solve(int sta){
o=0,e=0;
e[1][1]=1,o[n*2+1][n*2+1]=o[n+1][n*2+1]=1;//e={0,1}
for(int i=1;i<=n;i++) o[i+n][i]=1;
for(int i=1;i<=g.cnt;i++){
//(u,v)=>f[n][u]=f[n-1][v]+f[n-2][v]
int u=g[i].u,v=g[i].v;
o[u+n][v+n]++;
if(u==1) e[1][v+n]++;
if((~sta&g[i].w)==0) o[u][v+n]++;
}
return (e*(o^t))[1][n*2+1];
}
int main(){
// #ifdef LOCAL
// freopen("input.in","r",stdin);
// #endif
tb['B']=1,tb['J']=2,tb['M']=4,tb['P']=8;
scanf("%d%d",&n,&m);
for(int i=1,u,v;i<=m;i++) scanf("%d%d%s",&u,&v,buf+1),g.add(u,v,has(buf));
scanf("%d",&t);
int all=solve(15),res=0;
for(int i=1;i<=15;i++) res+=solve(15-i)*(popcount(i)&1?1:-1);//,printf("ban=%d,ans%c=%d\n",i,"-+"[popcount(i)&1],solve(15-i));
// printf("all=%d,res=%d\n",all,res);
printf("%d\n",((all-res)%P+P)%P);
return 0;
}
/*
t in s => ~s&t==0
*/
复杂度:\(O(2^kn^3\log T)\),其中 \(k=4\) 为商品种类数。
本文来自博客园,作者:caijianhong,转载请注明原文链接:https://www.cnblogs.com/caijianhong/p/solution-P5188.html


