题解 LOJ6738【王的象棋世界】

problem

一个 \(R\times C\) 的棋盘，你有 \(Q\) 组询问，每次询问国王走 \(R-1\) 步从 \((1,a)\) 到达 \((R,b)\) 有多少种方案。你只需要输出答案对 \(998244353\) 取模的结果。\(2\le C\le 10^5, C\le R\le 10^9, 1\le Q\le 10^5\)。

solution

首先 DP 和矩阵优化 DP 都比较简单，但是跑不动 1e5：\(f_{i,j}=f_{i-1,j-1}+f_{i-1,j}+f_{i-1,j+1}\)。这个矩阵不是循环矩阵，不太能做。他离循环矩阵就差几个数。主要是边界拦住了我们的去路。

考虑消除边界的影响，我们考虑这么一个东西：

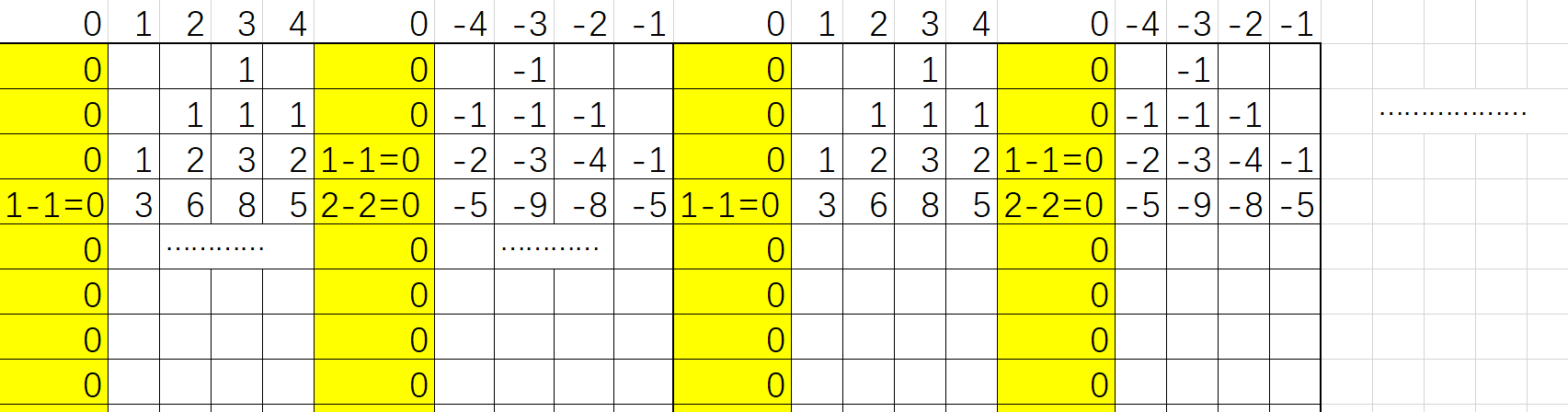
我们在最左边放了一列零，然后是正常的 DP 数组，然后又是一列零，然后接着 DP 数组取相反数之后倒过来的数组（foldl (\acc v -> (-v):acc) [] dp），这两中无限循环下去。当两个相邻的 DP 数组撞在一起时，它们会因为相反数从而全部变成零，中间那一列全部是零。这样再看，那个 DP 数组就没有边界影响了。

为了能算，我们只保留前两个 DP 数组，长度为 \(len=2m+2\)，并强制他在 \([0,len)\) 中循环转移（下标 \(\bmod len\)），这样就对起来了。把这个转移矩阵写成多项式，做循环卷积（\(\bmod (x^{len}-1)\)，这是基于 \(x^{len}\bmod (x^{len}-1)=1\)），跑出它的 \(n-1\) 次幂。询问的时候是一个两项的多项式乘一个多项式循环卷积后拿出移项系数，那么这是 \(O(1)\) 的。总复杂度为 \(O(m\log m\log n+Q)\)。

另外这个东西叫 反射容斥 。这 是一篇博客，从无数个将军饮马的角度说明了反射容斥，得出的东西和上述无区别。

code

点击查看代码

#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr,##__VA_ARGS__)
#else
#define debug(...) void(0)
#endif
typedef long long LL;
int glim(int x){return 1<<(32-__builtin_clz(x));}
int bitctz(int x){return __builtin_ctz(x);}
template<unsigned P> struct modint{
    unsigned v; modint():v(0){}
    template<class T> modint(T x):v((x%int(P)+int(P))%int(P)){}
    modint operator-()const{return modint(P-v);}
    modint inv()const{return qpow(*this,LL(P)-2);}
    modint&operator+=(const modint&rhs){if(v+=rhs.v,v>=P) v-=P; return *this;}
    modint&operator-=(const modint&rhs){return *this+=-rhs;}
    modint&operator*=(const modint&rhs){v=1ull*v*rhs.v%P; return *this;}
    modint&operator/=(const modint&rhs){return *this*=rhs.inv();}
    friend int raw(const modint&self){return self.v;}
    friend modint qpow(modint a,LL b){modint r=1;for(;b;b>>=1,a*=a) if(b&1) r*=a; return r;}
    friend modint operator+(modint lhs,const modint&rhs){return lhs+=rhs;}
    friend modint operator-(modint lhs,const modint&rhs){return lhs-=rhs;}
    friend modint operator*(modint lhs,const modint&rhs){return lhs*=rhs;}
    friend modint operator/(modint lhs,const modint&rhs){return lhs/=rhs;}
    friend bool operator==(const modint&lhs,const modint&rhs){return lhs.v==rhs.v;}
    friend bool operator!=(const modint&lhs,const modint&rhs){return lhs.v!=rhs.v;}
};
const int P=998244353,G=3;
typedef modint<998244353> mint;
void ntt(vector<mint>&a,int op){
    int n=a.size(); vector<mint> w(n);
    for(int i=1,r=0;i<n;i++){
        int b=bitctz(n)-bitctz(i);
        r&=(1<<b)-1,r^=1<<(b-1);
        if(i<r) swap(a[i],a[r]);
    }
    for(int k=1,len=2;len<=n;k<<=1,len<<=1){
        mint wn=qpow(op==1?mint(G):mint(1)/G,(P-1)/len);
        for(int i=raw(w[0]=1);i<k;i++) w[i]=w[i-1]*wn;
        for(int i=0;i<n;i+=len){
            for(int j=0;j<k;j++){
                mint x=a[i+j],y=a[i+j+k]*w[j];
                a[i+j]=x+y,a[i+j+k]=x-y;
            }
        }
    }
    if(op==-1){mint inv=mint(1)/n; for(mint&x:a) x*=inv;}
}
int n,m,Q,len;//mod (x^len-1)
vector<mint> multiple(vector<mint> a,vector<mint> b){
    int n=a.size(),m=b.size(),l=glim(n+m-1);
    a.resize(l),ntt(a,1);
    b.resize(l),ntt(b,1);
    for(int i=0;i<l;i++) a[i]*=b[i];
    ntt(a,-1);
    for(int i=len;i<l;i++) a[i-len]+=a[i];
    a.resize(len);
    return a;
}
vector<mint> qpow(vector<mint> a,int b){
    vector<mint> r={1};
    for(;b;b>>=1,a=multiple(a,a)) if(b&1) r=multiple(r,a);
    return r;
}
int main(){
//  #ifdef LOCAL
//      freopen("input.in","r",stdin);
//  #endif
    scanf("%d%d%d",&n,&m,&Q),len=m*2+2;
    vector<mint> f(len);
    f[0]=f[1]=f[len-1]=1;
#ifdef LOCAL
    f.resize(glim(len));
    ntt(f,1),ntt(f,-1);
    for(auto&x:f) debug("%d ",raw(x));
    debug("\n");
#endif
    f=qpow(f,n-1);
    for(int a,b,t=1;t<=Q;t++){
        scanf("%d%d",&a,&b);
        //A=x^a-x^{len-a}
        //ans=[x^b](A*f) (mod x^len-1)
        auto mod=[&](int x)->int{return (x%len+len)%len;};
        printf("%d\n",raw(f[mod(b-a)]-f[mod(b+a)]));
    }
    return 0;
}