题解 HDU3629【Convex】

计算几何大杂侩！今天是平面几何，明天呢？

problem

平面上 \(n\) 个点满足两点不重合，三点不共线，求有多少个凸的四边形。\(n\leq 700\)。

以下 prework 会的同学可以跳过（）就我不会（）

prework：三角函数初步

~~（好吧就今天中午刚学的做个学习笔记而已）~~

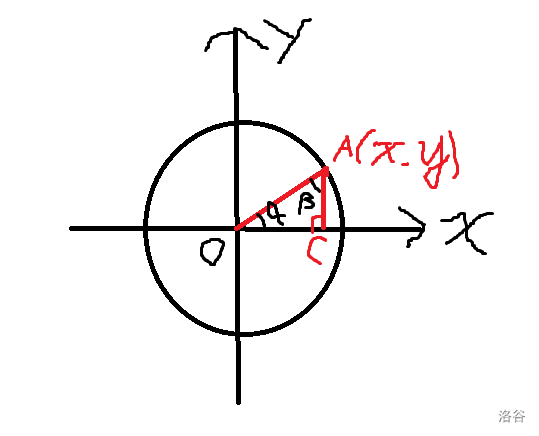
如图在平面直角坐标系中，\(\bigodot O\) 的半径为 \(1\)，点 \(A(x,y)\) 在圆上，\(AC\perp OC\) 与点 \(C\)。这意味着 \(OC=x,AC=y\)，对吗？

三角函数的定义

\(\sin\alpha\) 表示以 \(\alpha\) 为一个角的直角三角形中 对边比斜边 的比值。
\(\cos\alpha\) 表示以 \(\alpha\) 为一个角的直角三角形中 邻边比斜边 的比值。
\(\tan\alpha\) 表示以 \(\alpha\) 为一个角的直角三角形中 对边比邻边 的比值。

这个定义是可以推广的，只要是个角就行。

性质一：三角函数与单位圆

\(\sin\alpha=\frac{AC}{OA}=\frac{y}{1}=y\)。
\(\cos\alpha=\frac{OC}{OA}=\frac{x}{1}=x\)。
\(\tan\alpha=\frac{AC}{OC}=\frac{y}{x}\)。不在单位圆上也适用。~~结论：\(\tan\) 是意外，\(\sin,\cos\) 才是一对~~

也就是说 \(A(\cos\alpha,\sin\alpha)\)，同时 \(\tan\alpha=\frac{\sin\alpha}{\cos\alpha}\)。

性质二：三角函数与勾股定理

由勾股定理得，\(AC^2+OC^2=OA^2\)（即 \(x^2+y^2=1\) 发现了吗？），也就是 \(\sin^2\alpha+\cos^2\alpha=1\)。

性质三：三角函数的增减性

随着点 \(A\) 的移动，在 \(0^\circ<\alpha<90^\circ\)（\(0<\alpha<\frac{\pi}{2}\)）时，随着点 \(A\) 的纵坐标增加，显然横坐标在递减，也就是说：

\(x\) 递减：\(\cos\alpha\) 递减。
\(y\) 递增：\(\sin\alpha\) 递增。
\(\tan\alpha=\frac{y}{x}\) 递增。

性质四：三角函数余角公式

在图中我们声明了 \(\beta=\angle OAC\)，显然因为是直角三角形所以 \(\alpha+\beta=\frac{\pi}{2}\)，观察：

\(\sin\beta=x=\cos\alpha=\frac{OC}{OA}\)。
\(\cos\beta=y=\sin\alpha=\frac{AC}{OA}\)。
\(\tan\beta\cdot\tan\alpha=1\)。

差不多了。

prework：极角排序与 `std::atan2`

给平面选定一个原点，那么每个点都能以方位角 + 距离的形式被唯一的表示。我们称所谓的方位角为极角。

现在对于一个点 \(A(x,y)\)，我们要求它的极角，即 \(OA\) 与 \(x\) 轴的夹角，怎么求呢？

刚刚说了 \(\tan\alpha=\frac{y}{x}\)，我们相当于求一个 \(\alpha\) 使得 \(\tan\alpha=\frac{y}{x}\)。

这里用 \(\tan\) 的反函数 \(\arctan\) 求出 \(\alpha\)。在 C++ 标准库中已经有一个 std::atan2 可以使用，调用 atan2(y,x) 即可求出它的极角。在这里我们不太关心正负，只要有序的转一圈就行了，不用刻意的调整。

prework：极角排序与叉积

我们只要它绕一圈就行了，要求不高。考虑叉积。

这里我们先确定这个点的象限，如果象限不同比较编号，否则直接叉积，看一下是否大于零。

sort(b+1,b+n+1,[&](dot<LL> a,dot<LL> b){
			auto quad=[](dot<LL> a){
				if(a.x>0&&a.y>=0) return 0;
				if(a.x<=0&&a.y>0) return 1;
				if(a.x<0&&a.y<=0) return 2;
				if(a.x>=0&&a.y<0) return 3;
				return -1; 
			};
			return quad(a)==quad(b)?a*b>0:quad(a)<quad(b);
		});

prework：向量

定义

~~为了写程序方便~~，引入向量 \(\vec{a}=(x,y)\)。\(\vec{a}\) 本质上是一个点的偏移量，因此我们不关心它的起点是什么，可以减，例如两个点 \(A=(x_1,y_1),B=(x_2,y_2)\)，有向线段可以表示为向量 \(\vec{AB}=(x_2-x_1,y_2-y_1)\)。注意到令 \(O=(0,0)\) 为原点，\(\vec{OA}=(x,y)=A\) 因此向量可以用点的方式存储。

令 \(\vec{a}=(x_1,y_1),\vec{b}=(x_2,y_2)\)，定义一些运算：

向量模长：\(|\vec{a}|=\sqrt{x^2+y^2}\).
向量加法：\(\vec{a}+\vec{b}=(x_1+x_2,y_1+y_2)\)。
向量减法：\(\vec{a}-\vec{b}=(x_1-x_2,y_1-y_2)\)。
向量数乘：\(\lambda\vec{a}=(\lambda x,\lambda y)\)。
向量点乘：\(\vec{a}\cdot\vec{b}=x_1x_2+y_1y_2\)。
向量叉乘：\(\vec{a}\times\vec{b}=x_1y_2-x_2y_1\)。

叉积

重点看叉积，我们声明其符号为 \(\times\)：

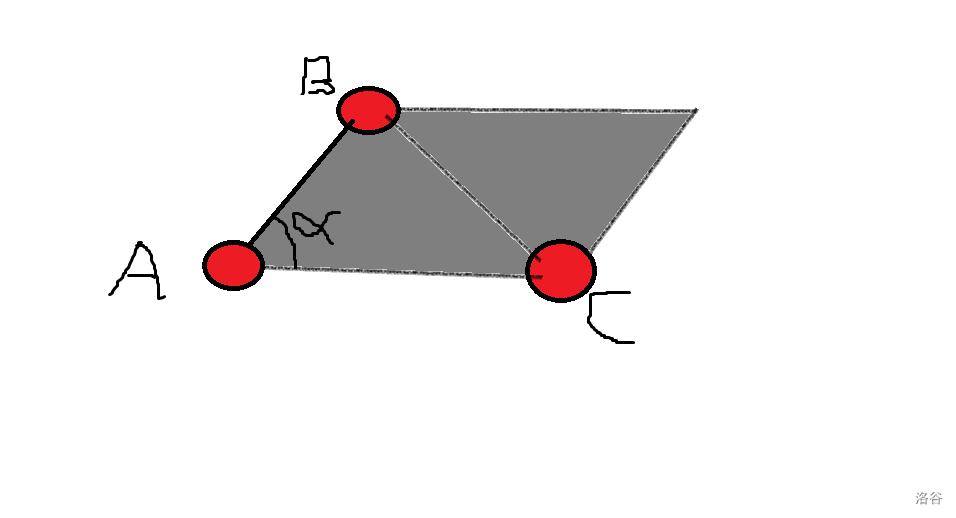
如图，当 \(\alpha\leq180^\circ\) 时，\(\vec{AC}\times\vec{AB}\geq 0\)，也就是这个灰色的平行四边形的面积，或者说是：

\(\vec{AC}\) 绕点 \(A\) 逆时针旋转到 \(\vec{AB}\) 所扫过的平行四边形的面积。

如果反过来 \(\vec{AB}\times\vec{AC}\leq 0\) 就是 \(\vec{AB}\) 反过来（顺时针）转到 \(\vec{AC}\) 扫过的平行四边形面积的相反数。

以下是一些小性质：

\(\vec a\times\vec b=X_aY_b-X_bY_a\)（定义）。
两个起点不同的向量要叉乘，可以将其中一个向量平移，使两个向量起点相同就可以叉乘。
\(\vec a\times \vec b=-\vec b\times\vec c\)。没有交换律。
\(a//b\Leftrightarrow\vec a\times \vec b=0\)。

这里提供一个板子：

template<class T=double> struct dot{
	T x,y;
	dot(T x=0,T y=0):x(x),y(y){}
	dot operator+(dot b){return dot(x+b.x,y+b.y);}//向量加
	dot operator-(dot b){return dot(x-b.x,y-b.y);}//向量减
	dot operator*(T k){return dot(x*k,y*k);}//数乘，或叫放缩
	T operator*(dot b){return x*b.y-b.x*y;}//叉乘
	T operator^(dot b){return x*b.x+y*b.y;}//点乘，对应坐标相乘
	friend T dist(dot a){return sqrt(a^a);}//绝对值 / 模长，即到原点的距离
};

solution 0：\(O(n^4)\)

复习一下凸多边形的判定：选定一条边后，其它所有点都在这条边所在的直线的同一侧。

于是可以用叉积写出暴力了（）

具体一点：点 \(A,B,C,D\)，枚举 \(\vec{AB}\) 是一条边，则 \(\vec{AB}\times\vec{AC}\) 与 \(\vec{AB}\times\vec{AD}\) 符号相同（注意到三点不共线）。

注意一些小细节：算重 \(8\) 次（枚举每条边和方向）

Code

typedef long long LL;
template<class T=double> struct dot{
	T x,y;
	dot(T x=0,T y=0):x(x),y(y){}
	dot operator+(dot b){return dot(x+b.x,y+b.y);}
	dot operator-(dot b){return dot(x-b.x,y-b.y);}
	dot operator*(T k){return dot(x*k,y*k);}
	T operator*(dot b){return x*b.y-b.x*y;}
	T operator^(dot b){return x*b.x+y*b.y;}
	friend T dist(dot a){return sqrt(a^a);}
};
int n;
dot<LL> a[510];
LL ans=0;
bool check(int i,int j,int x,int y){
	auto sgn=[](LL x)->int{return !x?0:(x<0?-1:1);};
	return sgn((a[j]-a[i])*(a[x]-a[i]))*sgn((a[j]-a[i])*(a[y]-a[i]))>0;
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%lld%lld",&a[i].x,&a[i].y);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			if(i==j) continue;
			for(int k=1;k<=n;k++){
				if(i==k||j==k) continue;
				for(int l=1;l<=n;l++){
					if(l==i||l==j||l==k) continue;
					ans+=check(i,j,k,l)&&check(j,k,l,i)&&check(k,l,i,j)&&check(l,i,j,k);
				}
			}
		}
	}
	printf("%lld\n",ans>>3);
	return 0;
}

solution 1：\(O(n^3)\)

考虑不算凸四边形，我们算凹（āo）四边形的数量。

枚举两个点 \(A,B\)，再找两个点 \(C,D\)，如果 \(C,D\) 在 \(AB\) 所在直线的异侧就说明四边形 \(ABCD\) 一定不是凸四边形，而是凹四边形。

所以枚举两个点，记 \(AB\) 左边（任意一边都行）有 \(c_0\) 个点，右边有 \(c_1\) 个点，则贡献 \(c_0\cdot c_1\) 个凹四边形。

而四边形一共有 \(\binom{n}{4}\) 个，所以答案是四边形的个数减去凹四边形的个数。

Code

typedef long long LL;
template<class T=double> struct dot{
	T x,y;
	dot(T x=0,T y=0):x(x),y(y){}
	dot operator+(dot b){return dot(x+b.x,y+b.y);}
	dot operator-(dot b){return dot(x-b.x,y-b.y);}
	dot operator*(T k){return dot(x*k,y*k);}
	T operator*(dot b){return x*b.y-b.x*y;}
	T operator^(dot b){return x*b.x+y*b.y;}
	friend T dist(dot a){return sqrt(a^a);}
};
int n;
LL ans;
dot<LL> a[510];
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%lld%lld",&a[i].x,&a[i].y);
	ans=1ll*n*(n-1)*(n-2)*(n-3)>>3; 
	for(int i=1;i<=n;i++){
		for(int j=i+1;j<=n;j++){
			LL cnt[2]={0,0};
			for(int k=1;k<=n;k++){
				if(i==k||j==k) continue;
				debug("i=%d,j=%d,k=%d,*=%lld\n",i,j,k,(a[k]-a[j])*(a[i]-a[j]));
				if((a[k]-a[j])*(a[i]-a[j])>0) cnt[0]++;
				else cnt[1]++; 
			}
			ans-=cnt[0]*cnt[1];
		}
	}
	printf("%lld\n",ans);
	return 0;
}

solution 2：\(O(n^2\log n)\)

还是考虑求凹四边形，考虑它的形状，大概是一个三角形（三角形没有凹凸之分）里面有一个点的样子。

枚举三角形的中心点，现在我们要找有多少个三角形包含它。

还是容斥：总方案数是 \(\binom{n-1}{3}\)，要求不包含中心点的三角形。

假设中心点是 \(O\)，枚举一个点 \(A\)，作直线 \(OA\)。在 \(OA\) 一侧的点，选出两个，加上点 \(A\) 就是一个三角形。正确的，因为不存在三点共线。

考虑极角排序之后，点 \(A\) 继续往下枚举，这条直线也在旋转，枚举所有点之后刚好转一圈，于是可以维护这条直线转到哪（类似单调队列优化），一遍扫过去，均摊的线性。

极角排序使用喜欢的算法做（）但是判断平角这个部分可以说一下：

叉乘的写法是 a*b>0。
std::atan2 的写法是 angle(a,b)<PI，其中 \(PI=\pi=\arccos(-1)\)，angel 求两个角度的差，注意写法：
```
double angel(double a,double b){
  return a>=b?a-b:a-b+2*PI; 
}
```
要判一下减爆的情况，加个周角 \(2\pi\)。

Code（`std::atan2`）

#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr,##__VA_ARGS__)
#else
#define debug(...) void(0)
#endif
typedef long long LL;
const double PI=acos(-1);
LL C(LL n,int m){
	switch(m){
		case 1: return n;
		case 2: return n*(n-1)/2;
		case 3: return n*(n-1)/2*(n-2)/3;
		case 4: return n*(n-1)/2*(n-2)/3*(n-3)/4;
	}
	return -1;
}
template<class T=double> struct dot{
	T x,y;
	dot(T x=0,T y=0):x(x),y(y){}
	dot operator+(dot b){return dot(x+b.x,y+b.y);}
	dot operator-(dot b){return dot(x-b.x,y-b.y);}
	dot operator*(T k){return dot(x*k,y*k);}
	T operator*(dot b){return x*b.y-b.x*y;}
	T operator^(dot b){return x*b.x+y*b.y;}
	friend T dist(dot a){return sqrt(a^a);}
};
int n;
dot<LL> a[510];
double b[510];
double angel(double a,double b){
	return a>=b?a-b:a-b+2*PI; 
}
LL calc(int n){//不包含中心点的凸三角形个数 
	LL ans=0;
	for(int l=1,r=0;l<=n;l++){//枚举一个点 
		while(r+1<l+n&&angel(b[r%n+1],b[l])<PI) r++;//不超过一个平角 
		ans+=C(r-l,2);
	}
	return ans;
}
LL solve(){//凹包个数 
	LL ans=0;
	for(int i=1;i<=n;i++){//枚举中转点 
		for(int j=1;j<=n;j++) if(i!=j) b[j-(j>i)]=atan2(a[j].y-a[i].y,a[j].x-a[i].x);
		sort(b+1,b+n);
		ans+=C(n-1,3)-calc(n-1);
	}
	return ans;
}
int main(){
//	#ifdef LOCAL
freopen("trick.out","w",stdout);
freopen("trick.in","r",stdin);
//	#endif
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%lld%lld",&a[i].x,&a[i].y);
	printf("%lld\n",C(n,4)-solve());
	return 0;
}

Code（叉积）

#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr,##__VA_ARGS__)
#else
#define debug(...) void(0)
#endif
typedef long long LL;
const double PI=acos(-1);
LL C(LL n,int m){
	switch(m){
		case 1: return n;
		case 2: return n*(n-1)/2;
		case 3: return n*(n-1)/2*(n-2)/3;
		case 4: return n*(n-1)/2*(n-2)/3*(n-3)/4;
	}
	return -1;
}
template<class T=double> struct dot{
	T x,y;
	dot(T x=0,T y=0):x(x),y(y){}
	dot operator+(dot b){return dot(x+b.x,y+b.y);}
	dot operator-(dot b){return dot(x-b.x,y-b.y);}
	dot operator*(T k){return dot(x*k,y*k);}
	T operator*(dot b){return x*b.y-b.x*y;}
	T operator^(dot b){return x*b.x+y*b.y;}
	friend T dist(dot a){return sqrt(a^a);}
};
int n;
dot<LL> a[510],b[510];
LL sgn(LL x){return !x?0:(x<0?-1:1);}
LL calc(int n){//不包含中心点的凸三角形个数 
	LL ans=0;
	for(int l=1,r=0;l<=n;l++){//枚举一个点 
		while(r+1<l+n&&b[l]*b[r%n+1]>=0) r++;//不超过一个平角 
		//注意自己叉自己是合法的 
		ans+=C(r-l,2);
	}
	return ans;
}
LL solve(){//凹包个数 
	LL ans=0;
	for(int i=1;i<=n;i++){//枚举中转点 
		for(int j=1;j<=n;j++) if(i!=j) b[j-(j>i)]=a[j]-a[i];
		sort(b+1,b+n,[&](dot<LL> a,dot<LL> b){
			auto quad=[](dot<LL> a){
				if(a.x>0&&a.y>=0) return 0;
				if(a.x<=0&&a.y>0) return 1;
				if(a.x<0&&a.y<=0) return 2;
				if(a.x>=0&&a.y<0) return 3;
				return -1; 
			};
			return quad(a)==quad(b)?a*b>0:quad(a)<quad(b);
		});
//		for(int j=1;j<n;j++) printf("%.3lf\n",atan2(b[j].y,b[j].x));
//		puts("=======");
//调试小细节：如果你写对了，这里输出 atan2 的值应该是两个递增的序列拼在一起
		ans+=C(n-1,3)-calc(n-1);
	}
	return ans;
}
int main(){
//	#ifdef LOCAL
	 	freopen("trick.in","r",stdin);
//	#endif
freopen("trick.out","w",stdout);
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%lld%lld",&a[i].x,&a[i].y);
	printf("%lld\n",C(n,4)-solve());
	return 0;
}

solution 3：\(O(n^3\log n)\)

枚举对角线，左右两边的点分别求出夹角 \((\alpha_x,\beta_x)\)，那么相当于要找两个在异侧的点满足 \(\alpha_x+\alpha_y<\pi\land\beta_x+\beta_y<\pi\)。

CDQ 分治。

posted @ 2022-11-14 19:51 caijianhong 阅读(50) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部