题解 Gym 104077I【[ICPC2022 Xi'an R] Square Grid】

题解 Gym 104077I【[ICPC2022 Xi'an R] Square Grid】

problem

二维棋盘，边界是 \((0,0)\) 到 \((n,n)\)。

对于某个棋子，单次移动可以朝着上下左右四个方向之一移动一格。

对于 \(q\) 个独立的棋子，分别问时间 \(T\) 秒以后：

  • 第 \(i\) 个棋子，起始位置在 \((x_0, y_0)\)，最终落到了 \((x_1, y_1)\)，则其有多少种行动方案数。

\(n,q\leq 10^5\)。\(T\) 是所有询问固定，\(T\leq 10^9\)。

solution 1D

如果这个题是一维的能做吗？能的。两种角度去考虑这个问题：

dp 角度（以 LOJ 6738 为例）

你考虑 dp，那这个题是不是说 \(f_{t, i}=f_{t - 1, i - 1} + f_{t - 1, i} + f_{t - 1, i + 1}\) 大概长这样，但是因为边界问题，不能用些什么东西优化，非常烦人。这时候反射容斥出来说，可以容斥。

假设我们现在的边界是 \([1,n]\)，那么考虑这么一个事情，就是说将 dp 数组左边接一列零，右边接一列零和它的相反数的翻转，无限接下去，就是大概这样：

img

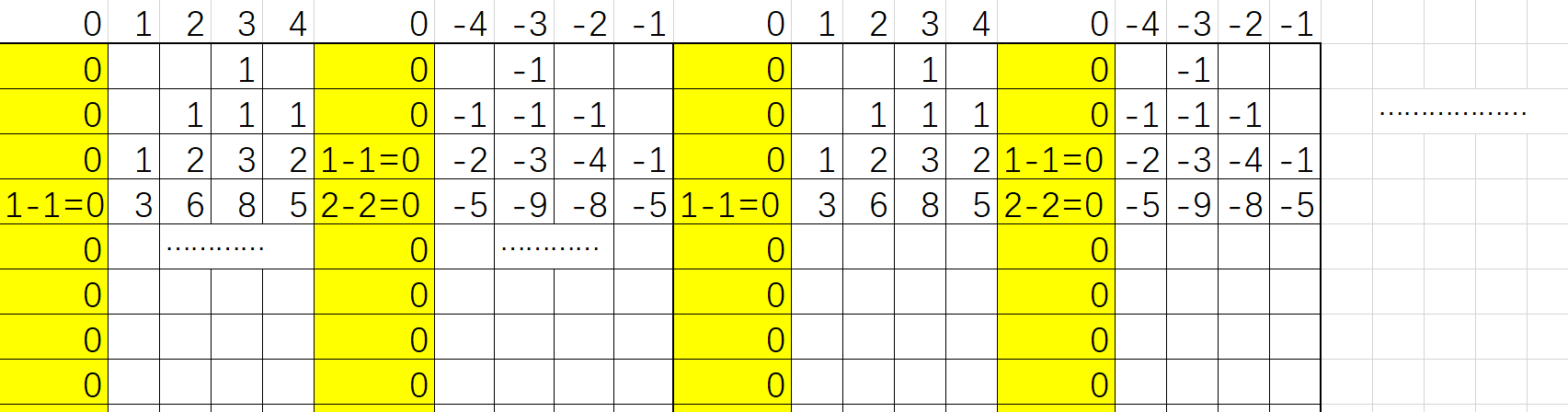
然后这样子可以发现原来的 dp 数组会在分界线被对称的相反数 dp 数组撞掉，刚好抵消变成 \(0\)，这样可以看作消除了边界的影响。

同时发现每两个框的 dp 数组都是一样的，不妨直接并起来只取前两个（前 \(2n+2\) 个数字），然后让他循环起来，下标 \(2n+2\) 的地方直接当做下标 \(0\) 的地方，于是可以做矩阵快速幂了。然后因为这是个循环矩阵，还不如直接将每一行的 dp 刻画成多项式，做多项式快速幂的循环卷积（多项式乘法在 \(\bmod (x^{2n+2}-1)\) 意义下进行，这样就有 \(x^{-1}\equiv x^{2n+1}\)）。算完以后可以 \(O(1)\) 回答，需要同时考虑 起点 和 起点的对称点 对终点的贡献。

将军饮马角度

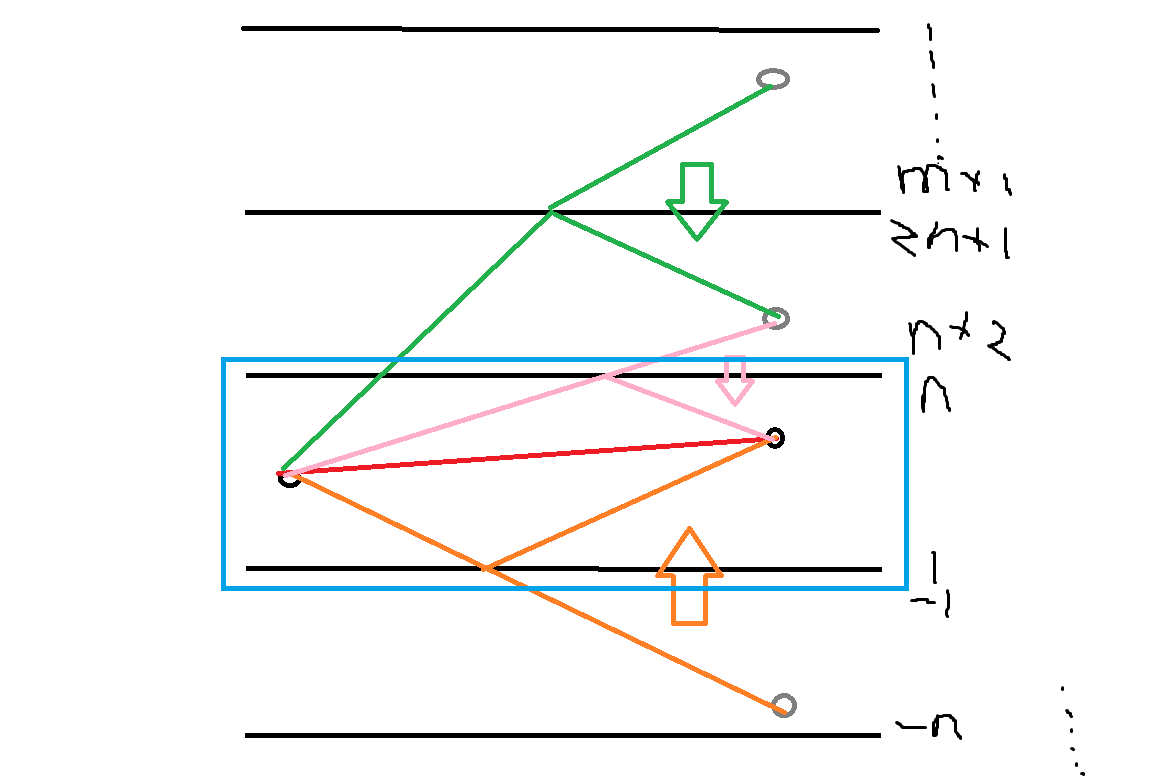
我们可以把它当作将军饮马问题，就是做对称，然后 \(i\) 到 \(j\) 的方案数等于 \(i\to j\) 的，减去 \((2n+2-i)\to j\)（\(+2\) 是为了修正对称；以下记 \(m=2n+2\)），加上 \((i+m)\to j\) 的方案数，当然反过来往负数方向去也要。

为什么是这样？你每次踩到 \(n+1\) 这个地方，就将前面的路径全部关于 \(n+1\) 对称一次，然后这些非法的路径，如果不考虑左边界，就和 \(m-i\) 到终点的所有路径形成双射。为了求出 \(m-i\) 不踩左边界的方案数，相当于是我要求他不踩 \(m\) 这条线的方案数，于是和刚才的东西一模一样，直到他没有那么多的步数可以去踩边界。

总之就是看起始点做了多少次对称，做奇数次对称对答案贡献为负，做偶数次对称对答案贡献为正。本质上我们是考虑 \(i+km\) 和 \(km - i\) 的所有点（\(k\in \mathbb Z\)），根据 \(i\) 的符号决定容斥系数，并尝试一口气算出这些点的全部贡献。所以这个算法叫做反射容斥。然后你尝试实现算的过程就和上面一样了。

总结

我们的核心点是关于 \(k(n+1)\)（其中 \(k\in \mathbb Z\)）做对称，考虑对称完的所有点，分类算出答案。

solution 2D

好的你已经完全掌握一维的情况了，现在请考虑二维吧。

二维的难点在于，我们可能需要去枚举上下走的具体步数，将上下走和左右走拆开，分别做反射容斥。但是步数特别大，反射容斥的式子也不像能卷起来的。

所以我们考虑将坐标变换一下 \((x,y)\to(x+y,x-y)\)（曼哈顿距离转切比雪夫距离，旋转 \(45\) 度）。这样的话我们的操作就相当于是 \(x\) 轴要走一步，同时 \(y\) 轴也要走一步，这样两维就独立了。但是，可能有更加严重的边界问题，例如你这样旋转之后边界就成斜线了，然后 \(x\) 坐标范围甚至和 \(y\) 有关，不好做，我们换一个角度。

我们考虑对终点做对称，每一维都做对称，这样对称出来形如 \((f_xx+k_xm,f_yy+k_ym)\)（这里 \(m=2n+2\)，\(k\in\mathbb Z,f\in\{\pm 1\}\)）的点，我们分开考虑。这个时候我们的棋盘就没有限制了，是无限大了，因为考虑了所有可能的反射点。例如我们拎出 \((x+km,y+lm)\) 来考虑，我们在这个没有约束的棋盘上走，首先做刚才 \((x, y)\to(x + y, x - y)\) 的变换，变成形如 \((x_1+km+y_1+lm-x_0-y_0,x_1+km-y_1-lm-x_0+y_0)\) 的东西，拆开看 \(x\) 维，记 \(a=x_1+y_1-x_0-y_0\)，然后我们在 \(x\) 这一维就要走 \(T\) 步，偏移量必须是 \(a+km-lm\)，每一步形如 \(\pm1\)。那么我最终写出来的东西就是：

\[\binom{T}{\frac 1 2 (T+a+(k-l)m)} \]

下面那个是 \(+1\) 的次数，这是一个方程组（\(c+d=T,c-d=a+(k-l)m\)），然后这个 binom 就能算出这个点的贡献，乘上容斥系数即可。

我们可以对 \(k-l\) 这个东西发起思考，先考虑一下 \(k\equiv l\pmod 2\) 的情况，那么这时式子变成：

\[\binom T {\frac{T+a}{2}+\frac{k-l}{2}m}\to\binom T {\frac{T+a}{2}+im}\to[x^{(T+a)/2}](1+x)^T\bmod(x^m-1). \]

出现了循环卷积形式（我们同时考虑了所有符号是正，\(k\equiv l\pmod 2\) 的点，同时计算了答案）。所以其他的点就能同理了。一共八种情况。

最终算法流程

  1. \(n:=n+1,m=2n+2\)。
  2. 求出 \(F=(1+x)^T\bmod (x^m-1)\)。
  3. 对于一组询问 \(x_0,y_0,x_1,y_1\)，如果 \(x_0,y_0,x_1,y_1,T\) 全部异或起来是奇数那么奇偶性错误没有方案。
  4. 枚举 \(x_1,y_1\) 的符号，枚举 \(k,l\) 是否同奇偶。
  5. 将新的 \(x',y'\) 传进另一个函数里，对于两个维度计算出 \(a=x'+y'-x_0-y_0,b=x'-y'-x_0+y_0\)，然后拿出 \([x^{(T+a)/2}]F\cdot [x^{(T+b)/2}]F\) 作为答案。
  6. 容斥系数是 \(x_1,y_1\) 的符号相乘。

更多思考

这个题如果不是正方形可能是做不了的，因为边界问题很烦人，如果考虑一个点在循环的对角线上走，只有正方形才能保证循环的对角线长度是边长，其它的矩形有可能使得循环的对角线长度变成和面积数值相同。

所谓的两维度独立，大概长这样，这也就大概解释了为什么循环卷积对着 \(m\) 做。

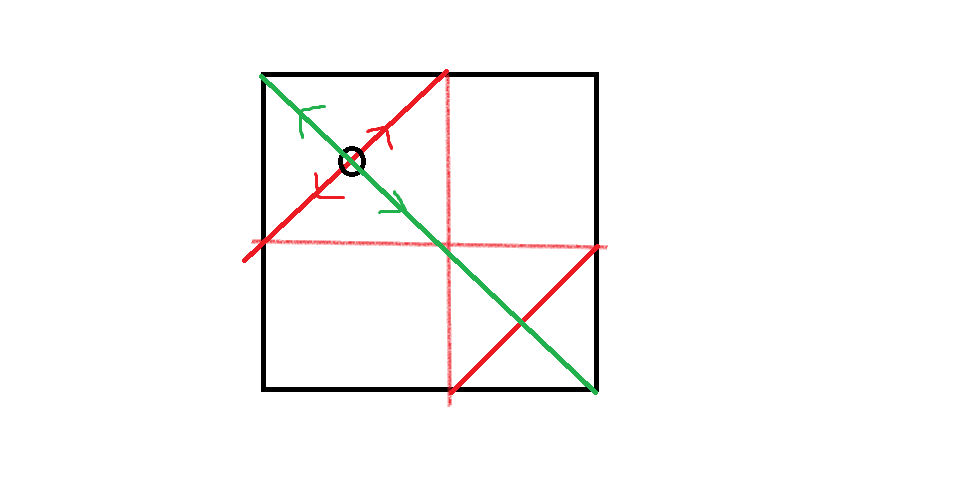
这个题如果扩展到三维可能是做不了的，因为我们无法使得三个维度都独立（三个维度独立有 \(2^3\) 种走法，然而三维里面只有 \(2\times 3\) 种走法。）同理，三维曼哈顿距离与三维切比雪夫距离，编者认为难以转换，因为三维曼哈顿球是正八面体，三维切比雪夫球是正方体。

code

#include <algorithm>
#include <cassert>
#include <cstdio>
#include <cstring>
#include <vector>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define debug(...) void(0)
#endif
typedef long long LL;
template <unsigned P>
struct modint {
    unsigned v;
    modint() : v(0) {}
    template <class T>
    modint(T x) : v((x % int(P) + int(P)) % int(P)) {}
    modint operator-() const { return modint(P - v); }
    modint inv() const { return assert(v), qpow(*this, LL(P) - 2); }
    modint& operator+=(const modint& rhs) {
        if (v += rhs.v, v >= P) v -= P;
        return *this;
    }
    modint& operator-=(const modint& rhs) { return *this += -rhs; }
    modint& operator*=(const modint& rhs) {
        v = 1ull * v * rhs.v % P;
        return *this;
    }
    modint& operator/=(const modint& rhs) { return *this *= rhs.inv(); }
    friend int raw(const modint& self) { return self.v; }
    friend modint qpow(modint a, LL b) {
        modint r = 1;
        for (; b; b >>= 1, a *= a)
            if (b & 1) r *= a;
        return r;
    }
    friend modint operator+(modint lhs, const modint& rhs) {
        return lhs += rhs;
    }
    friend modint operator-(modint lhs, const modint& rhs) {
        return lhs -= rhs;
    }
    friend modint operator*(modint lhs, const modint& rhs) {
        return lhs *= rhs;
    }
    friend modint operator/(modint lhs, const modint& rhs) {
        return lhs /= rhs;
    }
    friend bool operator==(const modint& lhs, const modint& rhs) {
        return lhs.v == rhs.v;
    }
    friend bool operator!=(const modint& lhs, const modint& rhs) {
        return lhs.v != rhs.v;
    }
};
int glim(int x) { return 1 << (32 - __builtin_clz(x)); }
int bitctz(int x) { return __builtin_ctz(x); }
const int P = 998244353, G = 3;
typedef modint<998244353> mint;
void ntt(vector<mint>& a, int op) {
    int n = a.size();
    vector<mint> w(n);
    for (int i = 1, r = 0; i < n; i++) {
        int b = bitctz(n) - bitctz(i);
        r &= (1 << b) - 1, r ^= 1 << (b - 1);
        if (i < r) swap(a[i], a[r]);
    }
    for (int k = 1, len = 2; len <= n; k <<= 1, len <<= 1) {
        mint wn = qpow(op == 1 ? mint(G) : mint(1) / G, (P - 1) / len);
        for (int i = raw(w[0] = 1); i < k; i++) w[i] = w[i - 1] * wn;
        for (int i = 0; i < n; i += len) {
            for (int j = 0; j < k; j++) {
                mint x = a[i + j], y = a[i + j + k] * w[j];
                a[i + j] = x + y, a[i + j + k] = x - y;
            }
        }
    }
    if (op == -1) {
        mint inv = mint(1) / n;
        for (mint& x : a) x *= inv;
    }
}
// vector<mint> multiple(vector<mint> a, vector<mint> b, int m) {
//     int len = glim(a.size() + b.size() - 1);
//     a.resize(len), b.resize(len);
//     ntt(a, 1), ntt(b, 1);
//     for (int i = 0; i < len; i++) a[i] *= b[i];
//     ntt(a, -1);
//     for (int i = m; i < len; i++) a[i % m] += a[i];
//     a.resize(m);
//     return a;
// }
// vector<mint> qpow(vector<mint> a, int b, int m) {
//     vector<mint> res = {1};
//     for (; b; b >>= 1, a = multiple(a, a, m)) {
//         if (b & 1) res = multiple(res, a, m);
//     }
//     return res;
// }
//需要优化一下 ntt 次数
vector<mint> qpow(vector<mint> a, int b, int m) {
    int len = glim(m * 2);
    vector<mint> res = {1};
    for (; b; b >>= 1) {
        a.resize(len), ntt(a, 1);
        if (b & 1) {
            res.resize(len), ntt(res, 1);
            for (int i = 0; i < len; i++) res[i] *= a[i];
            ntt(res, -1);
            for (int i = m; i < len; i++) res[i % m] += res[i];
            res.resize(m);
        }
        for (int i = 0; i < len; i++) a[i] *= a[i];
        ntt(a, -1);
        for (int i = m; i < len; i++) a[i % m] += a[i];
        a.resize(m);
    }
    return res;
}
int main() {
    //#ifdef LOCAL
    //    freopen("in", "r", stdin);
    //#endif
    int n, T, Q, m;
    scanf("%d%d%d", &n, &T, &Q);
    n += 1, m = 2 * n + 2;
    vector<mint> f = qpow({1, 1}, T, m);
    for (auto x : f) debug("%d, ", raw(x));
    while (Q--) {
        int x1, y1, x2, y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        x1 += 1, y1 += 1, x2 += 1, y2 += 1;
        if ((x1 ^ y1 ^ x2 ^ y2 ^ T) & 1) {
            puts("0");
            continue;
        }
        auto mod = [m](int x) -> int { return (x % m + m) % m; };
        auto solve = [&](int x2, int y2) -> mint {
            int dx = x2 + y2 - x1 - y1 + T, dy = x2 - y2 - x1 + y1 + T;
            return f[mod(dx >> 1)] * f[mod(dy >> 1)];
        };
        mint res = 0;
        for (int i : {1, -1})
            for (int j : {1, -1})
                res +=
                    i * j * (solve(i * x2, j * y2) + solve(m + i * x2, j * y2));
        printf("%d\n", raw(res));
    }
    return 0;
}

全文共 2873 词，8457 字符。

posted @ 2023-09-23 21:06  caijianhong  阅读(82)  评论(0)  编辑  收藏  举报