题解 ARC142E【Pairing Wizards】

problem

给定 \(n\) 个元素，每个元素有两个属性 \(a_i, b_i\)。

你可以花费 1 的代价使得其中一个元素的 \(a\) 属性 +1。

问最少多少代价，可以使得给定的 \(m\) 组 \((i,j)\) 关系符合：

• 要么满足 \(a_i >= b_i \land a_j >= b_j\)；
• 要么满足 \(a_i >= b_j \land a_j >= b_i\)。

• \(2 \leq N \leq 100\)
• \(1 \leq a_i,b_i \leq 100\)
• \(1 \leq M \leq \frac{N(N-1)}{2}\)
• \(1 \leq x_i \lt y_i \leq N\)
• \((x_i,y_i) \neq (x_j,y_j)\), if \(i\neq j\).
• All values in input are integers.

solution

限制相当于 \(\max(a_i, a_j)\geq \max(b_i, b_j)\land\min(a_i, a_j)\geq \min(b_i, b_j)\)。我们通过强制调整使得第二个限制被满足（直接将 \(\min(b_i, b_j)\) 分别对 \(a_i, a_j\) chkmax），这样只需要考虑第一个限制。这时候就有：\(a_i\geq b_i\) 或者 \(a_i\geq b_j\)，如果 \(a_i\geq b_i\land a_j\geq b_j\) 跳过，否则就是其中有一个 \(a_i\geq b_i\)，另外一个 \(a_i\leq a_j<b_j\)。我们将 \(a_i\geq b_i\) 划归 A 类点，\(a_i<b_i\) 划归 B 类点，则限制是在 A 类点和 B 类点之间的边，竟然是二分图。

于是对于 \(\max(a_i, a_j)\geq \max(b_i, b_j)\)，因为后面是常数，所以我们可以做最小割。

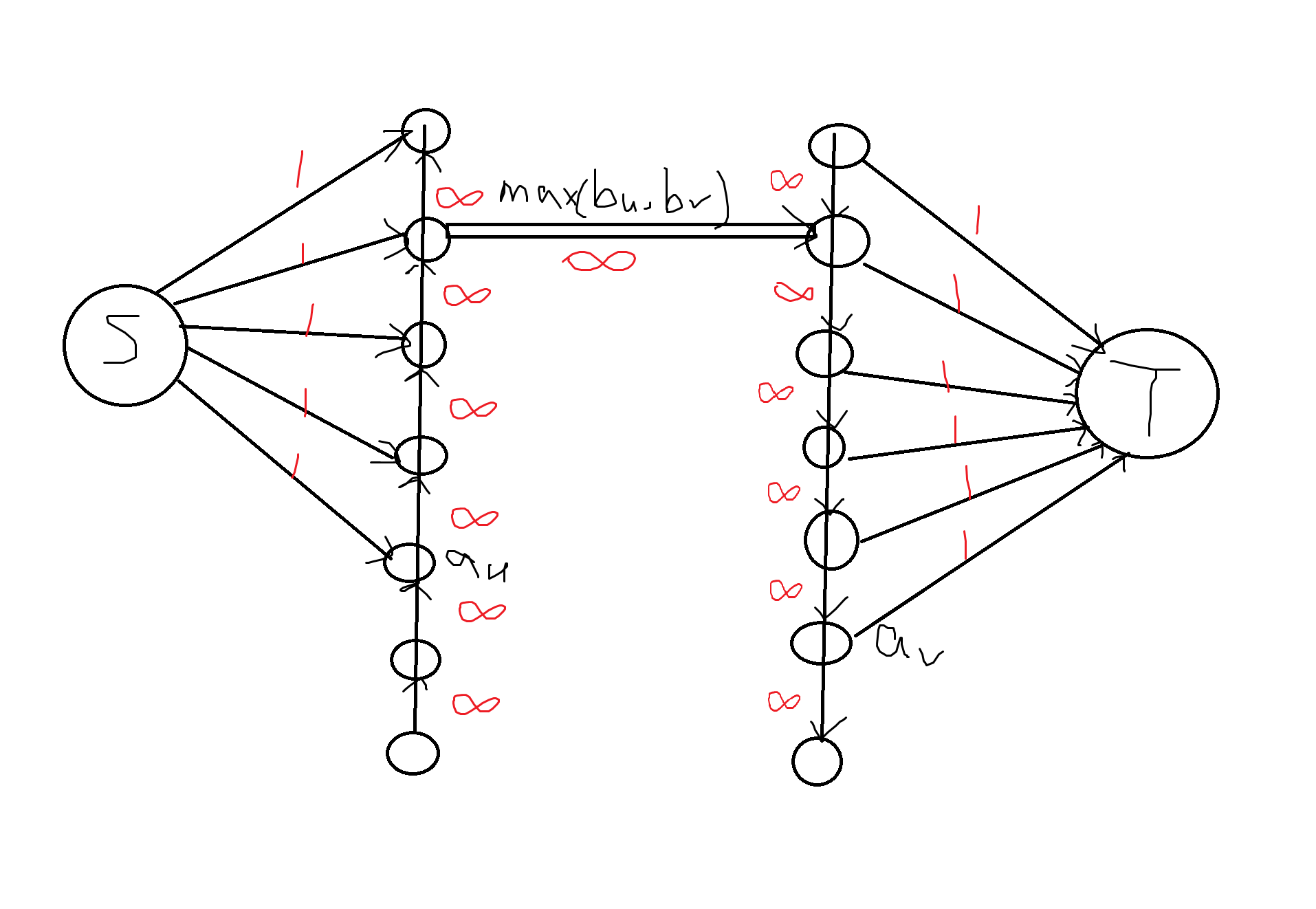
S 连 A 类点，T 连 B 类点，左边正链右边反链，就能完成题目限制。红色数字是边权。切完以后刚好是这样的。非常优美。

code

#include <queue>
#include <cstdio>
#include <vector>
#include <cstring>
#include <cassert>
#include <algorithm>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define debug(...) void(0)
#endif
typedef long long LL;
typedef long long LL;
template<int N,int M,class T=int> struct graph{
    int head[N+10],nxt[M*2+10],cnt,tot;
    struct edge{
        int u,v;T w;
        edge(int u=0,int v=0,T w=0):u(u),v(v),w(w){}
    } e[M*2+10];
    graph(){memset(head,tot=cnt=0,sizeof head);}
    edge& operator[](int i){return e[i];}
    void add(int u,int v,T w=0){e[++cnt]=edge(u,v,w),nxt[cnt]=head[u],head[u]=cnt;}
    void link(int u,int v,T w=0){add(u,v,w),add(v,u,w);}
};
template<int N,int M,class T=int> struct maxflow_g:public graph<N,M,T>{
	graph<N,M,T>&g=*this;
	maxflow_g(){g.add(0,0,0);}
	void insert(int u,int v,T w){debug("%d %d %d\n", u, v, w), g.add(u,v,w),g.add(v,u,0);}
	int dep[N+10],cur[N+10];
	bool bfs(int s,int t){
		queue<int> q; memset(dep,0x3f,sizeof dep);
		for(q.push(s),dep[s]=0;!q.empty();){
			int u=q.front(); q.pop();
			for(int i=g.head[u];i;i=g.nxt[i]){
				int v=g[i].v; if(!g[i].w) continue;
				if(dep[v]>dep[u]+1) q.push(v),dep[v]=dep[u]+1;
			}
		}
        return dep[t]!=dep[0];
	}
	T dfs(int u,T flow,int t){
		if(u==t||!flow) return flow;
		T rest=flow;
		for(int &i=cur[u];i;i=g.nxt[i]){
			int v=g[i].v; if(dep[v]!=dep[u]+1||!g[i].w) continue;
			T run=dfs(v,min(rest,g[i].w),t);
			if(g[i].w-=run,g[i^1].w+=run,!(rest-=run)) break;
		}
		if(rest==flow) dep[u]=-1;
        return flow-rest;
	}
	T maxflow(int s,int t,T inf){
		T flow=0;
		while(bfs(s,t)) memcpy(cur,g.head,sizeof cur),flow+=dfs(s,inf,t);
		return flow;
	}
};
int n, a[110], b[110], c[110], id[110][110], m;

int V = 100;
bool islimed[110][110];
maxflow_g<100010, 300010, int> g;
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%d%d", &a[i], &b[i]), c[i] = a[i];
    scanf("%d", &m);
    for (int i = 1, u, v; i <= m; i++) {
        scanf("%d%d", &u, &v);
        islimed[u][v] = islimed[v][u] = 1;
        a[u] = max(a[u], min(b[u], b[v]));
        a[v] = max(a[v], min(b[u], b[v]));
    }
    int S = ++g.tot, T = ++g.tot;
    for (int i = 1; i <= n; i++) {
        //debug(">>> i = %d\n", i);
        //id[i][j - 1] <=> id[i][j] is the real edge
        if (a[i] < b[i]) {
            for (int j = 0; j <= V; j++) id[i][j] = ++g.tot;
            g.insert(S, id[i][0], 1e9), g.insert(id[i][V], T, 1e9);
            for (int j = 1; j < a[i]; j++) g.insert(id[i][j - 1], id[i][j], 1e9);
            for (int j = a[i]; j <= V; j++) g.insert(id[i][j - 1], id[i][j], j - c[i]);
        } else {
            for (int j = 1; j <= V + 1; j++) id[i][j] = ++g.tot;
            g.insert(S, id[i][V + 1], 1e9), g.insert(id[i][1], T, 1e9);
            for (int j = 1; j < a[i]; j++) g.insert(id[i][j + 1], id[i][j], 1e9);
            for (int j = a[i]; j <= V; j++) g.insert(id[i][j + 1], id[i][j], j - c[i]);
        }
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            if (!islimed[i][j]) continue;
            if ((a[i] >= b[i] && a[j] >= b[j]) || (a[i] >= b[j] && a[j] >= b[i])) continue;
            if (a[i] >= b[i]) continue;
            //a[i] < b[i], a[j] >= b[j]
            int maxb = max(b[i], b[j]);
            g.insert(id[i][maxb], id[j][maxb - 1], 1e9);
            g.insert(id[j][maxb], id[i][maxb - 1], 1e9);
        }
    }
    printf("%d\n", g.maxflow(S, T, 1e9));
    return 0;
}

#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define endl "\n"
#define debug(...) void(0)
#endif
typedef long long LL;
template <class T>
struct graph {
  struct edge {
    int u, v;
    T w;
  };
  vector<edge> e;
  vector<int> head, nxt;
  edge& operator[](int i) { return e[i]; }
  edge operator[](int i) const { return e[i]; }
  graph(int n = 0) : head(n, -1) {}
  size_t size() const { return head.size(); }
  void add(int u, int v, T w = T{}) {
    nxt.push_back(exchange(head[u], e.size()));
    e.push_back((edge){u, v, w});
  }
  void link(int u, int v, T w = T{}) { add(u, v, w), add(v, u, w); }
  int newnode() { head.push_back(-1); return head.size() - 1; }
};
template <class Cap>
struct mf_graph {
  graph<Cap> g;
  vector<int> dep, cur;
  mf_graph(int n = 0) : g(n) {}
  int newnode() { return g.newnode(); }
  void add(int u, int v, Cap cap) { debug("%d %d %d\n", u, v, cap), g.add(u, v, cap), g.add(v, u, 0); }
  bool bfs(int s, int t) {
    dep.assign(g.size(), -1);
    queue<int> q;
    q.push(s);
    dep[s] = 0;
    while (!q.empty()) {
      int u = q.front();
      q.pop();
      for (int i = g.head[u]; ~i; i = g.nxt[i]) {
        int v = g[i].v;
        if (g[i].w && dep[v] == -1) dep[v] = dep[u] + 1, q.push(v);
      }
    }
    return dep[t] != -1;
  }
  Cap dfs(int u, Cap flw, int t) {
    if (u == t) return flw;
    Cap res = flw;
    for (int& i = cur[u]; ~i; i = g.nxt[i]) {
      int v = g[i].v;
      if (g[i].w && dep[v] == dep[u] + 1) {
        Cap run = dfs(v, min(res, g[i].w), t);
        g[i].w -= run, g[i ^ 1].w += run;
        res -= run;
        if (!res) break;
      }
    }
    if (res == flw) dep[u] = -1;
    return flw - res;
  }
  Cap flow(int s, int t, Cap lim = numeric_limits<Cap>::max()) {
    Cap flw = 0;
    while (lim && bfs(s, t)) {
      cur = g.head;
      Cap run = dfs(s, lim, t);
      flw += run, lim -= run;
    }
    return flw;
  }
};
int n, a[110], b[110], ans, m, tot, id[110];
bool vis[110][110];
mf_graph<int> mf(10010);
int main() {
#ifndef LOCAL
  cin.tie(nullptr)->sync_with_stdio(false);  
#endif
  cin >> n;
  for (int i = 1; i <= n; i++) cin >> a[i] >> b[i], ans -= a[i];
  cin >> m;
  for (int i = 1; i <= m; i++) {
    int u, v;
    cin >> u >> v;
    vis[u][v] = vis[v][u] = true;
    a[u] = max(a[u], min(b[u], b[v]));
    a[v] = max(a[v], min(b[u], b[v]));
  }
  int s0 = tot++, t0 = tot++, V = 100;
  for (int i = 1; i <= n; i++) {
    ans += a[i];
    tot += V;
    id[i] = tot;
    if (a[i] >= b[i]) {
      for (int j = 1; j < V; j++) mf.add(tot - j, tot - j - 1, 1e9);
      for (int j = a[i] + 1; j <= V; j++) mf.add(s0, tot - j, 1);
    } else {
      for (int j = 1; j < V; j++) mf.add(tot - j - 1, tot - j, 1e9);
      for (int j = a[i] + 1; j <= V; j++) mf.add(tot - j, t0, 1);
    }
  }
  for (int i = 1; i <= n; i++) {
    for (int j = i + 1; j <= n; j++) {
      if (!vis[i][j]) continue;
      if (a[i] >= b[i] && a[j] >= b[j]) continue;
      if (a[i] >= b[j] && a[j] >= b[i]) continue;
      int mx = max(b[i], b[j]);
      if (a[i] >= b[i]) mf.add(id[i] - mx, id[j] - mx, 1e9);
      else mf.add(id[j] - mx, id[i] - mx, 1e9);
    }
  }
  debug("ans = %d\n", ans);
  cout << ans + mf.flow(s0, t0) << endl;
  return 0;
}