树上技术总结

目录

尝试总结一下树上数据结构的技术！结论是失败了，还有太多缺口在其中。

多次路径信息查询

\(C\) 是合并一次信息的复杂度。

  • 重链剖分： \(O(Cn)-O(C\log n)\)
    • 如果两端都不是根，则会有个隐藏的线段树在里面，不重要。
  • 点分治：\(O(Cn\log n)-O(C+\log n)\)。
    • 注意这个 \(O(\log n)\) 是求点分树 LCA 的复杂度，可以使用倍增进一步优化。
  • 树上倍增：\(O(Cn\log n)-O(C\log n)\)。
    • 如果信息满足 \(x\oplus x=x\) 的性质，则信息合并可以缩减到 \(O(1)\) 次。
  • 带权并查集（Tarjan 算法）：\(O(Cn\log n)\)。
    • 平均复杂度 \(O(Cn\alpha (n))\)，可惜这是个离线算法。

杂项技巧

树上倍增

计算一个数组 \(anc[j][u]\) 表示 \(u\) 的 \(2^j\) 级祖先，可以求 LCA，可以求树上 \(k\) 级祖先。

dfn 序

可以将每个点的子树写为一段 dfn 序上的区间，还可以将 LCA 问题转化为 RMQ 问题，配合点分治可以解决包含根的树上背包问题。

可以配合 bfs 序做一些小邻域问题：旅行 (tour) - 题目详情 - 思+学堂

树的直径

树的直径是树上距离最远的两个点之间的路径。树的直径可能有很多，但它们都经过树的中心，也就是树的任意直径的中点（也可能那是边，但是这不重要）。

对一棵树，记非空点集 \(S\) 中距离最远的两个点为 \(\text{diam}(S)\)，则有：

  • 对非空点集 \(S, T\) 有 \(\text{diam}(S\cup T)\subseteq\text{diam}(S)\cup\text{diam}(T)\)。
  • 对非空点集 \(S\) 与任意点 \(u\) 有 \(\max_{x\in S}\text{dist}(x, u)=\max_{x\in \text{diam}(S)}\text{dist}(x, u)\)。

树的边带非负权时，以上结论也成立。

Kruskal 重构树

对任意的无向的边带权的图（包括树）运行 Kruskal 算法，每次合并两个连通块时新建一个节点，它的两个儿子为这两个连通块对应的节点，权值是这条边的权值。最后获得的二叉树就是 Kruskal 重构树，它的所有叶子是原树节点，非叶子上有一个权值。

  • 原图中两个点 \(u, v\) 之间路径最大值的最小值为重构树上 \(\text{LCA}(u, v)\) 的权值。
  • 重构树上如果叶子 \(u\) 的一个祖先 \(z\) 的权值为 \(w\)，则意味着原图上从 \(u\) 出发只走 \(\leq w\) 的边能到达的点的集合为 \(z\) 的重构树的子树中的叶子。

重链剖分、树上启发式合并、全局平衡二叉树

三者的联系

重链剖分提出了“轻边”的概念，从而将某个点到根的链拆分成 \(O(\log n)\) 段重链的前缀，并且使所有轻子树的大小之和控制在 \(O(n\log n)\)（这导出了树上启发式合并）。而全局平衡二叉树则更加深入地控制 \(\log n\)，通过将重链按照轻子树大小和的权值建立带权的二叉树，使整棵树对应的全局平衡二叉树的高度不超过 \(O(\log n)\)。

树上启发式合并

树上启发式合并（dsu on tree，另外吐槽一下这个鬼名字）的具体过程是，首先求出每个点的重儿子。然后去解决每个子树，首先递归轻儿子，记录需要合并上来的信息并清空，然后递归重儿子，不去清空重儿子信息而是去 keep 住它，再将刚才清空的轻儿子信息合并进来即可。注意需要满足轻儿子上来的信息的量和轻儿子子树大小成线性。

全局平衡二叉树

【模板】全局平衡二叉树 - caijianhong - 博客园

三者的对比

重链剖分实际上也是一种”链分治“，从根开始拉一条链，处理跨过链的路径或子树信息，然后分治下去处理，分治深度不超过 \(O(\log n)\)。相较于点分治的好处是这样的一条链对树上的父子关系破坏较小。

从课件里复制一段话：

对比重链剖分和 dsu on tree，我们发现，dsu on tree 实际上就是沿着重链从底向上扫描，并且维护重链上的信息。

相较于 dsu on tree，放到重链剖分的背景下看问题的优势是更加灵活——我们支付同样的 log n 因子代价，却可以对重链延伸出去的子树内做任何操作，不一定要自底向上合并。

相较于点/边分治，重链剖分虽然处理路径问题上还有点吃力（主要是 LCA 枚举的问题），但是其优点是忠实地保持了原树的层次结构。

不过 dsu on tree 也有它的优点：简单好想，容易直接在自底向上合并的过程中加入这个优化。

点分治、边分治、点分树、边分树

点分治

每次选择重心并将其提升为根，统计跨过重心的路径，然后删掉重心，在剩下的连通块中继续递归。递归深度不超过 \(O(\log n)\)。

点分治中，如果计算的是点集之间的交叉贡献，那么我们可以采用类似于 Huffman 树的合并方式（P1090 [NOIP 2004 提高组] 合并果子 的合并方式）。也即每次选取点数最少的两个点集，计算贡献并合并为一个，然后放回去继续合并流程。可以证明，倘若计算交叉贡献的复杂度线性于两个点集大小之和，则复杂度仍为 \(O(n \log n)\)。

如果计算的信息可以差分，则可以直接容斥。直接计算每个子树对整棵树的答案，再减去自己对自己的答案。

点分树

将每次分治的重心的父亲设置为上次分治的重心，形成一棵高度不超过 \(O(\log n)\) 的多叉树。

由于深度被控制住了，每个点的子树大小和为 \(O(n\log n)\)，每个点只有 \(O(\log n)\) 个祖先，这样可以使用一些暴力的方法，例如枚举祖先进行计算。注意这一段并不是什么废话。

点分树可以非常方便地在线处理单点的邻域。如果允许离线则可以直接点分治。

边分治

每次选择重（zhòng）边，统计跨过重边的路径，然后删掉重边，在剩下的两个连通块中继续递归。一条边是重边当且仅当它两端的子树大小的 \(\max\) 是其它边中最小的。如果树的最大度数不超过 \(3\)，则递归深度不超过 \(O(\log n)\)。

边分治的优势是它只有两个连通块的信息要合并，而不像一般的没有 Haffman 树的点分治。这就允许我们不做一些例如凸包合并的工作。

边分治对树的最大度数有苛刻的要求，主要是对菊花无能为力。可以将树进行三度化。将一个点的所有儿子拎出来，建任意一棵二叉树，树的根是这个点，所有叶子是它的所有儿子，并适当地将原树边权信息放在新的树上。

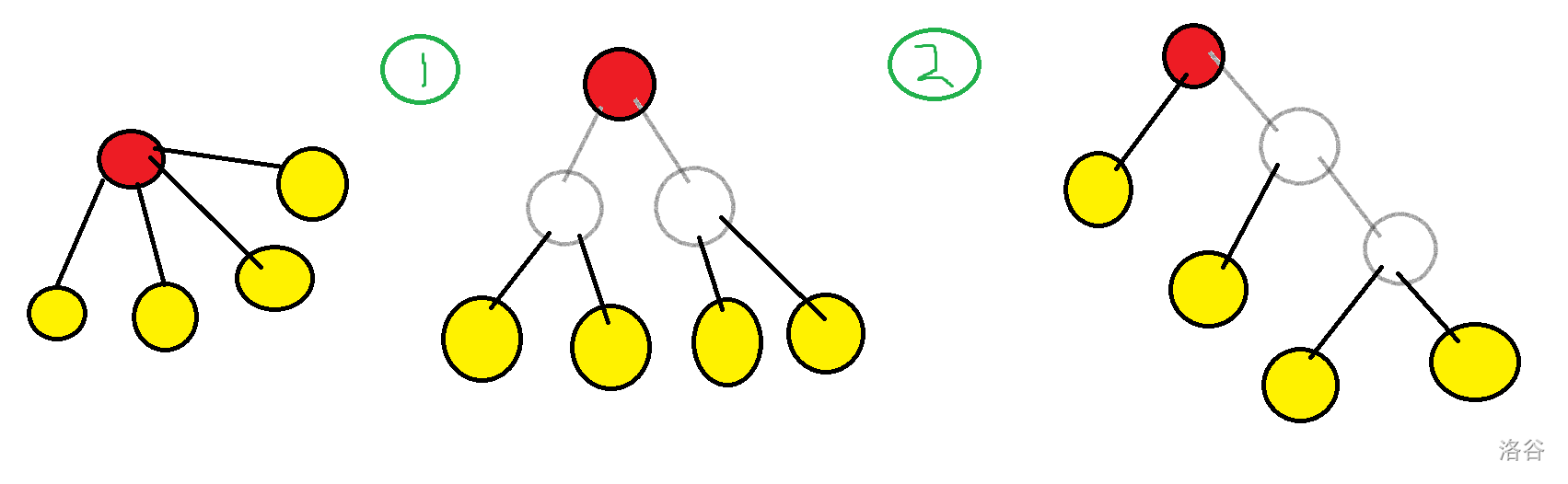
并不是所有的题目都可以三度化。

边分树

将每次分治的重边的父亲设置为上次分治的重边，形成一棵二叉树。如果树的最大度数不超过 \(3\)，则边分树高度不超过 \(O(\log n)\)。

由于边分树是二叉树，我们可以进行边分树合并。我们先改造一下这棵树，首先用原树的深度区分一下每条边的左右儿子，就让深度大的一侧的连通块为左儿子，另一侧为右儿子之类的。然后在现在是叶子的边的两侧再把它的两个端点挂上去，这样形成了一棵叶子是点，非叶子是边的有根二叉树，它的高度是 \(O(\log n)\)。

先明确问题，正如黄洛天论文中那样，如果我们有 \(n\) 个集合，第 \(i\) 个集合初始只有第 \(i\) 个点。每次合并两个集合 \(S, T\)，需要查询 \(u\in S, v\in T\) 的 \(\text{dist}(u, v)+a_u+a_v\) 的最大值。解法是对初始在每个集合拉出一条从第 \(i\) 个点在大边分树上到根的二叉树链。然后合并两棵边分树的时候就在重合的那条边上统计贡献，就和线段树合并差不多，复杂度也由线段树合并的证明保证。黄洛天论文里写的空间复杂度 \(O(n)\) 是因为它用了前文的那个空间优化，不写那个优化就是 \(O(n\log n)\) 的时空复杂度。

具体一点，对于边分树上的某条边，它的编号为 \(i\)，两个端点从深到浅为 \((u, v)\)，则记

\[Lmx_i=\max_{x\in \text{subtree}(ch[i][0])}\{\text{dist}(x, u)+a_x\} \]

\[Rmx_i=\max_{x\in \text{subtree}(ch[i][1])}\{\text{dist}(x, v)+a_x\} \]

注意，每个边的信息都是单独计算的，不是从它的左右儿子继承而来，但好在这个信息只需要计算一次，一共 \(O(n\log n)\)。之后合并的时候，如果两棵边分树上 \(u, v\) 指代同一条边权为 \(w\) 的边，则合并了左右子树后查询 \(\max(Lmx_i+Rmx_j, Lmx_j+Rmx_i)\)，然后将两边信息合并为 \(\max(Lmx_i, Lmx_j), \max(Rmx_i, Rmx_j)\)。

这时候就有个问题了，写了这么多为什么不直接合并连通块直径？？？然后你发现边分树可以处理边权为负的情况。

注意了！！！以上是我口胡的！！！

使用差分模拟 LCA 信息

例如 P4211 [LNOI2014] LCA 就是在做这样的事情。\(dep_{\text{LCA}(u, v)}\) 不好求，考虑差分，变成 \(u\) 到根的链 \(+1\)，查询 \(v\) 到链的和。这样的想法也能用在其它的题目中，省去很多麻烦。

长链剖分

基本概念

【模板】长链剖分 - caijianhong - 博客园

与重链剖分相似，长链剖分是将树剖成很多条长链。

我们定义长儿子，为一个点的儿子中子树深度最大的一个儿子。或者这样定义：

  • 给每个点一个 \(height_u\)。叶子节点的 \(height\) 为 \(1\)。
  • 则其它所有点的 \(height_u\) 定义为 \(\max_{v\in son}\{height_v\}+1\)，并记录取到 \(height_u\) 的儿子 \(v\) 为长儿子（保留一个）
  • 长链就是一条到叶节点的链，满足链上任意一个父亲的儿子是它的长儿子。

有几个性质值得留意：

  • 所有长链长度总和为 \(O(n)\)，因为每一个点都只在一个长链中。
  • 任意一个节点 \(x\) 的 \(k\) 级祖先 \(y\) 所在长链的长度一定大于等于 k，否则 \(y\) 所在长链应该接到 \(x\) 上去。
  • 从一个节点开始向上跳长链，最多跳 \(O(\sqrt{n})\) 次。因为每次跳到的长链长度一定是单调递增的。

长链剖分可以 \(O(n\log n)-O(1)\) 求 LCA、LA。

以下缩写 \(height_u\) 为 \(len_u\)，如果 \(u\) 是长链顶，那么 \(len_u\) 是这条长链的点数。另外还有不等式 \(len_u\geq len_v+1\)，证明请参见 \(len_u\) 的定义。

邻域

长链剖分最擅长做内向邻域相关的问题，就是一个点的子树内离它距离 \(\leq d\) 的范围，这和它的结构是一致的。

长链剖分也已经可以做其它邻域问题了，这详见 2025 年刘海峰的集训队论文。

有一个路径邻域问题可以用长链剖分解决：举办乘凉州喵，举办乘凉州谢谢喵 - Problem - QOJ.ac。

树分块

【模板】树分块（简单版）

int dvt(int u) { 
  int now = 1;
  for (int v : g[u]) if (v != fa[u]) now += dvt(v);
  if (now >= sqrt(n)) key[u] = true, now = 0;
  return now;
}

这种树分块只能保证一个块内的高度（最大深度）不超过 \(\sqrt n\)，以及关键点个数不超过 \(O(\sqrt n)\)，其它什么也保证不了，但确实是最好写的。

posted @ 2025-02-11 16:11  caijianhong  阅读(100)  评论(0)    收藏  举报