【模板】可持久化的 WBLT
【模板】可持久化的 WBLT
WBLT,also known as "Weight Balanced Leafy Tree",是一种平衡树(Tree),满足每个节点要么是叶子,要么有两个儿子(Leafy);在此基础上,WBLT 是加权平衡的,深度是严格 \(O(\log n)\)(Weight Balanced)。WBLT 支持 \(O(\log size)\) 的插入、删除,\(O(\log size)\) 查询排名、第 \(k\) 小、前驱、后继等信息,以及 \(O(\log size)\) 分裂,\(O(\log \frac{size_p}{size_q})\) 合并(其中 \(p, q\) 是要合并的两个子树,钦定 \(size_p>size_q\))。本文通过对若干资料的抄写,引入了可持久化的 WBLT。
Leafy Tree
基本操作
首先去掉加权平衡,说一说普通的 Leafy Tree 是怎样支持插入、删除、查询操作的。
我们在每个节点上,维护这个点左右儿子 \(ch[0], ch[1]\),这个点的子树大小 \(siz\)。在叶子节点上维护值 \(val\)。如果是普通平衡树,可以在非叶节点 \(p\) 上同时维护 \(val[p]=val[ch[p][1]]\)。
以下是新建节点(newnode)、判断一个节点是否为叶子(isleaf)和向上维护节点信息(一般是 pushup,在这里使用 maintain 代替,请注意不要混淆)的一个代码实现。
int ch[N << 1][2], val[N << 1], siz[N << 1], tot;
int newnode(int v, int q = 0) {
int p = ++tot;
val[p] = v;
siz[p] = 1;
ch[p][0] = ch[p][1] = 0;
return p;
}
bool isleaf(int p) { return !ch[p][0]; }
void maintain(int p) { // also known as: pushup
if (isleaf(p)) return ;
val[p] = val[ch[p][1]];
siz[p] = siz[ch[p][0]] + siz[ch[p][1]];
}
查询
以在节点 \(p\) 的子树中查询 \(v\) 的排名为例,在平衡树上根据 \(val[ch[p][0]]\) 即左子树最大值决定向哪一边递归。
int getrnk(int p, int v) {
int res = 0;
while (!isleaf(p)) {
// pushdown(p);
int r = val[ch[p][0]] < v;
if (r) res += siz[ch[p][0]];
p = ch[p][r];
}
return res + (val[p] < v);
}
(还未出现的操作用注释标记,后文引入操作后,它们标记了它们应该出现的位置。)
因为线段树也是一种 Leafy Tree,所以我们也可以用线段树的方法完成。这里略过。
插入
找到与插入值 \(v\) 最相近的叶子节点后,将叶子节点分裂,添加两个儿子。如果是在第 \(k\) 个数字之后插入值,也是类似的。
void insert(int p, int v) {
// pushdown(p);
// refresh(p);
if (isleaf(p)) {
ch[p][0] = newnode(val[p]);
ch[p][1] = newnode(v);
if (val[ch[p][0]] > val[ch[p][1]]) swap(ch[p][0], ch[p][1]);
} else {
insert(ch[p][val[ch[p][0]] < v], v);
}
maintain(p);
// update(p);
}
void insert(int &p, int v, int k) {
// pushdown(p);
// refresh(p);
int r = siz[ch[p][0]] < k;
if (isleaf(p)) {
ch[p][0] = newnode(val[p]);
ch[p][1] = newnode(v);
} else {
if (r) k -= siz[ch[p][0]];
insert(ch[p][r], v, k);
}
maintain(p);
// update(p);
}
删除
在父亲处找到节点后,删去这个节点,父亲只剩一个儿子,这时的操作是将父亲删去,用另一个儿子的信息替换父亲。
void erase(int &p, int v) {
// pushdown(p);
// refresh(p);
int r = val[ch[p][0]] < v;
if (isleaf(ch[p][r])) {
if (val[ch[p][r]] != v) return;
// destroy(ch[p][0]), destroy(ch[p][1]);
int q = ch[p][!r];
memcpy(ch[p], ch[q], sizeof ch[p]);
val[p] = val[q];
siz[p] = siz[q];
} else {
erase(ch[p][r], v);
}
maintain(p);
// update(p);
}
void erase(int &p, int k) {
// pushdown(p);
// refresh(p);
int r = siz[ch[p][0]] < k;
if (isleaf(ch[p][r])) {
// use[ch[p][0]] -= 1;
// use[ch[p][1]] -= 1;
clone(p, ch[p][!r]); // 实现和上面一样的操作,复制信息
} else {
if (r) k -= siz[ch[p][0]];
erase(ch[p][r], k);
}
maintain(p);
// update(p);
}
WBLT
平衡性
不妨直接定义每个节点的权重就是其子树大小。说一个点 \(p\) 是平衡的,当且仅当
其中 \(\alpha\) 是一个 \((0,\frac{1}{2}]\) 的常数,根据论文,取 \(\alpha=1-\sqrt2/2=0.29\) 较合理。
旋转
为了维护每个节点都是平衡的,引入旋转操作,旋转操作应该改变一些点的平衡性,同时不能改变其中序遍历。
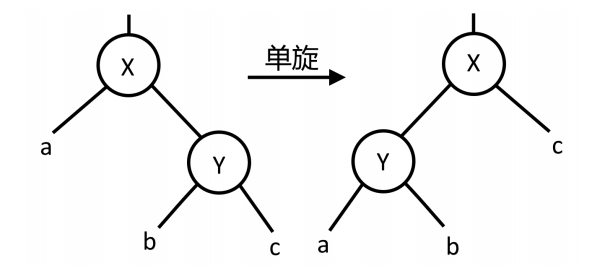
将节点 \(X\) 的右儿子 \(Y\) 旋转上来的示意图如上,注意这里同时交换了 \(X, Y\)。一个代码实现如下:
void rotate(int p, int r) { // 将节点 p 的 r 儿子(ch[p][r])旋转上来
if (isleaf(p) || isleaf(ch[p][r])) return;
// pushdown(ch[p][r]);
// refresh(ch[p][r]);
int q = ch[p][r];
swap(ch[p][0], ch[p][1]);
swap(ch[p][r], ch[q][r]);
swap(ch[q][0], ch[q][1]);
maintain(q);
maintain(p);
}
维护平衡
一个节点经过操作后,应该用一次单旋或一次双旋维护平衡。具体过程参见代码。证明不会,可以参见论文。
void update(int p) { // also known as: maintain
if (isleaf(p)) return;
int r = siz[ch[p][0]] < siz[ch[p][1]];
if (siz[ch[p][!r]] >= siz[p] * alpha) return;
// pushdown(ch[p][r]);
// refresh(ch[p][r]);
if (siz[ch[ch[p][r]][!r]] >= siz[ch[p][r]] * (1 - alpha * 2) / (1 - alpha))
rotate(ch[p][r], !r);
rotate(p, r);
}
代码
将上文关于 update 的注释去掉就得到了一份普通平衡树代码。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define debug(...) void(0)
#endif
typedef long long LL;
template <int N>
struct WBLT {
static constexpr double alpha = 0.292;
int ch[N << 1][2], val[N << 1], siz[N << 1], tot, root, tsh[N << 1], tct;
WBLT() { root = newnode(-1e9); }
bool isleaf(int p) { return !ch[p][0]; }
void destroy(int p) { tsh[++tct] = p; }
void maintain(int p) { // also known as: pushup
if (isleaf(p)) return ;
val[p] = val[ch[p][1]];
siz[p] = siz[ch[p][0]] + siz[ch[p][1]];
}
void rotate(int p, int r) {
if (isleaf(p) || isleaf(ch[p][r])) return ;
int &q = ch[p][!r];
swap(ch[p][0], ch[p][1]);
swap(ch[p][r], ch[q][r]);
swap(ch[q][0], ch[q][1]);
maintain(q);
maintain(p);
}
void update(int p) { // also known as: maintain
if (isleaf(p)) return ;
int r = siz[ch[p][0]] < siz[ch[p][1]];
if (siz[ch[p][!r]] >= siz[p] * alpha) return;
if (siz[ch[ch[p][r]][!r]] >= siz[ch[p][r]] * (1 - alpha * 2) / (1 - alpha))
rotate(ch[p][r], !r);
rotate(p, r);
}
int newnode(int v) {
int p = tct ? tsh[tct--] : ++tot;
val[p] = v;
ch[p][0] = ch[p][1] = 0;
siz[p] = 1;
return p;
}
void insert(int p, int v) {
if (isleaf(p)) {
ch[p][0] = newnode(val[p]);
ch[p][1] = newnode(v);
if (val[ch[p][0]] > val[ch[p][1]]) swap(ch[p][0], ch[p][1]);
} else {
insert(ch[p][val[ch[p][0]] < v], v);
}
maintain(p);
update(p);
}
void erase(int p, int v) {
int r = val[ch[p][0]] < v;
if (isleaf(ch[p][r])) {
if (val[ch[p][r]] != v) return;
destroy(ch[p][0]), destroy(ch[p][1]);
int q = ch[p][!r];
memcpy(ch[p], ch[q], sizeof ch[p]);
val[p] = val[q];
siz[p] = siz[q];
} else {
erase(ch[p][r], v);
}
maintain(p);
update(p);
}
int getrnk(int p, int v) {
int res = 0;
while (!isleaf(p)) {
int r = val[ch[p][0]] < v;
if (r) res += siz[ch[p][0]];
p = ch[p][r];
}
return res + (val[p] < v);
}
int getkth(int p, int k) {
k += 1;
while (!isleaf(p)) {
int r = k > siz[ch[p][0]];
if (r) k -= siz[ch[p][0]];
p = ch[p][r];
}
return val[p];
}
};
WBLT<100010> t;
int main() {
scanf("%*d");
for (int op, x; ~scanf("%d%d", &op, &x);) {
debug("op = %d, x = %d\n", op, x);
switch (op) {
case 1:
t.insert(t.root, x);
break;
case 2:
t.erase(t.root, x);
break;
case 3:
printf("%d\n", t.getrnk(t.root, x));
break;
case 4:
printf("%d\n", t.getkth(t.root, x));
break;
case 5:
x = t.getrnk(t.root, x) - 1, printf("%d\n", t.getkth(t.root, x));
break;
case 6:
x = t.getrnk(t.root, x + 1), printf("%d\n", t.getkth(t.root, x));
break;
}
}
return 0;
}
有必要加入一些适当的垃圾回收,具体是删除操作时删掉左右儿子。
使用洛谷 P3369 进行效率测试,笔者的各种平衡树的效率如下:
| 名称 | 时间 | 空间 | |
|---|---|---|---|
| WBLT | 208ms | 1.86MB | |
| Splay | 445ms | 13.46MB | |
| FHQ-Treap | 322ms | 1.38MB | |
| 替罪羊树 | 324ms | 2.47MB |
由于代码之间的常数有差异,这个结果没有太多参考价值,仅供参考。
文艺 WBLT
作为文艺平衡树,WBLT 需要支持区间翻转,基本的思路是将区间分裂出来,打上翻转标记,然后合并回去。所以就有了 rev[] 数组表示每个点的翻转标记,pushdown 是下放标记。
bool rev[N << 1];
void spread(int &p) {
if (isleaf(p)) return;
refresh(p);
rev[p] ^= 1;
}
void pushdown(int p) {
if (!rev[p] || isleaf(p)) return;
spread(ch[p][0]), spread(ch[p][1]);
swap(ch[p][0], ch[p][1]);
rev[p] = false;
}
合并
欲将合并两棵子树 \(p, q\),根据论文,我们进行如下分类讨论:
- 若 \(\min(siz[p], siz[q])\geq \alpha\times(siz[p]+siz[q])\),新建节点 \(t\),将 \(p, q\) 作为 \(t\) 的左右儿子。
- 否则钦定 \(siz[p]\geq siz[q]\),则
- 若 \(siz[ch[p][0]]\geq \alpha\times(siz[p]+siz[q])\),将 \(ch[p][1]\) 与 \(q\) 合并,再与 \(ch[p][0]\) 合并。
- 否则合并 \(ch[p][0], ch[ch[p][1]][0]\),再合并 \(ch[ch[p][1]][1], q\),最后合并前两次的结果。
int merge(int p, int q) {
if (!p || !q) return p + q;
if (min(siz[p], siz[q]) >= alpha * (siz[p] + siz[q])) {
int t = newnode(0);
ch[t][0] = p, use[p] += 1;
ch[t][1] = q, use[q] += 1;
maintain(t);
return t;
}
if (siz[p] >= siz[q]) {
pushdown(p);
if (siz[ch[p][0]] >= alpha * (siz[p] + siz[q])) {
return merge(ch[p][0], merge(ch[p][1], q));
} else {
pushdown(ch[p][1]);
return merge(merge(ch[p][0], ch[ch[p][1]][0]),
merge(ch[ch[p][1]][1], q));
}
} else {
pushdown(q);
if (siz[ch[q][1]] >= alpha * (siz[p] + siz[q])) {
return merge(merge(p, ch[q][0]), ch[q][1]);
} else {
pushdown(ch[q][0]);
return merge(merge(p, ch[ch[q][0]][0]),
merge(ch[ch[q][0]][1], ch[q][1]));
}
}
}
分裂
根据子树大小分裂,掰开左子树或右子树,然后用 merge 操作将剩下没掰开的子树合并起来。这是 \(O(\log siz)\) 的。
void split(int p, int k, int &x, int &y) {
if (!k) return x = 0, y = p, void();
if (isleaf(p)) return x = p, y = 0, void();
pushdown(p);
if (k <= siz[ch[p][0]]) {
split(ch[p][0], k, x, y);
y = merge(y, ch[p][1]);
} else {
split(ch[p][1], k - siz[ch[p][0]], x, y);
x = merge(ch[p][0], x);
}
}
代码
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define debug(...) void(0)
#endif
typedef long long LL;
template <int N>
struct WBLT {
static constexpr double alpha = 0.292;
int ch[N << 1][2], val[N << 1], siz[N << 1], tot, root, tsh[N << 1], tct;
WBLT() { root = newnode(-1e9); }
bool isleaf(int p) { return !ch[p][0]; }
void destroy(int p) { tsh[++tct] = p; }
void maintain(int p) { // also known as: pushup
if (isleaf(p)) return ;
val[p] = val[ch[p][1]];
siz[p] = siz[ch[p][0]] + siz[ch[p][1]];
}
bool rev[N << 1];
void spread(int p) {
rev[p] ^= 1;
}
void pushdown(int p) {
if (!rev[p] || isleaf(p)) return ;
spread(ch[p][0]), spread(ch[p][1]);
swap(ch[p][0], ch[p][1]);
rev[p] = false;
}
void rotate(int p, int r) {
if (isleaf(p) || isleaf(ch[p][r])) return ;
int q = ch[p][r];
pushdown(q);
swap(ch[p][0], ch[p][1]);
swap(ch[p][r], ch[q][r]);
swap(ch[q][0], ch[q][1]);
maintain(q);
maintain(p);
}
void update(int p) { // also known as: maintain
if (isleaf(p)) return ;
pushdown(p);
int r = siz[ch[p][0]] < siz[ch[p][1]];
if (siz[ch[p][!r]] >= siz[p] * alpha) return;
pushdown(ch[p][r]);
if (siz[ch[ch[p][r]][!r]] >= siz[ch[p][r]] * (1 - alpha * 2) / (1 - alpha))
rotate(ch[p][r], !r);
rotate(p, r);
}
int newnode(int v) {
int p = tct ? tsh[tct--] : ++tot;
val[p] = v;
ch[p][0] = ch[p][1] = 0;
siz[p] = 1;
return p;
}
void insert(int p, int v) {
if (isleaf(p)) {
ch[p][0] = newnode(val[p]);
ch[p][1] = newnode(v);
if (val[ch[p][0]] > val[ch[p][1]]) swap(ch[p][0], ch[p][1]);
} else {
pushdown(p);
insert(ch[p][val[ch[p][0]] < v], v);
}
maintain(p);
update(p);
}
void erase(int p, int v) {
pushdown(p);
int r = val[ch[p][0]] < v;
if (isleaf(ch[p][r])) {
if (val[ch[p][r]] != v) return;
destroy(ch[p][0]), destroy(ch[p][1]);
int q = ch[p][!r];
memcpy(ch[p], ch[q], sizeof ch[p]);
val[p] = val[q];
siz[p] = siz[q];
} else {
erase(ch[p][r], v);
}
maintain(p);
update(p);
}
int getrnk(int p, int v) {
int res = 0;
while (!isleaf(p)) {
pushdown(p);
int r = val[ch[p][0]] < v;
if (r) res += siz[ch[p][0]];
p = ch[p][r];
}
return res + (val[p] < v);
}
int getkth(int p, int k) {
k += 1;
while (!isleaf(p)) {
pushdown(p);
int r = k > siz[ch[p][0]];
if (r) k -= siz[ch[p][0]];
p = ch[p][r];
}
return val[p];
}
int merge(int p, int q) {
if (!p || !q) return p + q;
if (min(siz[p], siz[q]) >= alpha * (siz[p] + siz[q])) {
int t = newnode(0);
ch[t][0] = p, use[p] += 1;
ch[t][1] = q, use[q] += 1;
maintain(t);
return t;
}
if (siz[p] >= siz[q]) {
pushdown(p);
if (siz[ch[p][0]] >= alpha * (siz[p] + siz[q])) {
return merge(ch[p][0], merge(ch[p][1], q));
} else {
pushdown(ch[p][1]);
return merge(merge(ch[p][0], ch[ch[p][1]][0]),
merge(ch[ch[p][1]][1], q));
}
} else {
pushdown(q);
if (siz[ch[q][1]] >= alpha * (siz[p] + siz[q])) {
return merge(merge(p, ch[q][0]), ch[q][1]);
} else {
pushdown(ch[q][0]);
return merge(merge(p, ch[ch[q][0]][0]),
merge(ch[ch[q][0]][1], ch[q][1]));
}
}
}
void split(int p, int k, int &x, int &y) {
if (!k) return x = 0, y = p, void();
if (isleaf(p)) return x = p, y = 0, void();
pushdown(p);
if (k <= siz[ch[p][0]]) {
split(ch[p][0], k, x, y);
y = merge(y, ch[p][1]);
} else {
split(ch[p][1], k - siz[ch[p][0]], x, y);
x = merge(ch[p][0], x);
}
destroy(p);
}
void dfs(int p) {
pushdown(p);
if (isleaf(p)) {
if (val[p] > 0) cout << val[p] << " ";
else debug("-inf ");
} else {
dfs(ch[p][0]);
dfs(ch[p][1]);
}
}
void print(int p) {
if (!isleaf(p)) print(ch[p][0]),print( ch[p][1]);
debug("ch[%d] = {%d, %d}\n", p, ch[p][0], ch[p][1]);
}
};
WBLT<300010> t;
int main() {
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++) t.insert(t.root, i);
for (int i = 1; i <= m; i++) {
int l, r;
cin >> l >> r;
debug("l = %d, r = %d\n", l, r);
int x, y, z;
t.split(t.root, l, x, y);
t.split(y, r - l + 1, y, z);
t.spread(y);
t.root = t.merge(x, t.merge(y, z));
}
t.dfs(t.root), cout << endl;
return 0;
}
持久化文艺 WBLT
基本思路
鉴于平衡树一般都要维护信息和懒标记,这里跳过持久化 WBLT。将文艺 WBLT 修改为持久化的文艺 WBLT,可以使用路径复制,即将访问到的节点复制下来,形成一条路径。
懒标记
为了处理懒标记,我们这样考虑:因为在一棵持久化的 WBLT 上,一个点可能有多个父亲,但是儿子数量只能是 0 或 2 个。pushdown 的下放懒标记的操作,只会影响它的儿子,我们对一个点进行 pushdown,是没有影响的;反而是它的儿子,它的儿子可能不止它一个父亲,将它的标记下放到儿子,可能导致在别的父亲的版本上,多了一个不属于那个版本的懒标记,这就错了;除非它的儿子只有它一个父亲。所以我们应该在 pushdown 的时候,复制一遍儿子,把懒标记打到新的儿子上。
实现路径复制
在进行路径复制的时候,有一个想法是我们使用一个 refresh(p) 函数,表示把节点 \(p\) 复制一下,产生一个新的节点,重新赋值给 \(p\),这样比较好写;记得进入操作函数时传引用。使用 refresh 的原则是,如果它或它的儿子将要被修改,那么就 refresh,否则不需要;静态的查询,除了 pushdown 之外都不用 refresh。
pushdown 和 refresh 的顺序问题,如果保证什么操作都做路径复制,那么它们的顺序是无所谓的。
一个小优化
这里有一个优化。观察到 pushdown 的时候要复制两个节点,可以写标记永久化,但是刚才说了,如果它的儿子只有它一个父亲,可以不用复制。考虑记录每个节点有多少个父亲(认为每个版本的根都有一个父亲),记为 use。每次 refresh 的时候,如果 \(use\leq 1\) 则根本不用重建节点,否则新建节点并且 \(use\) 自减 \(1\) 表示父亲带着这个儿子跑了,父亲可以随意修改新的节点而不影响其它版本。另外每次复制节点的时候,如果节点有儿子,两个儿子的 \(use\) 自增 \(1\);合并两个子树时,返回的节点对两个儿子也有一个父亲的 \(use\);删除节点时,两个子节点都丢失一个父亲:这样能优化一些时空。
代码
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define endl "\n"
#define debug(...) void(0)
#endif
typedef long long LL;
template <int N>
struct WBLT {
static constexpr double alpha = 0.292;
int ch[N << 1][2], siz[N << 1], tot, root, tsh[N << 1], tct;
int val[N << 1];
LL sum[N << 1];
bool rev[N << 1];
int use[N << 1];
WBLT() { root = newnode(-(int)((1u << 31) - 1)); }
bool isleaf(int p) { return !ch[p][0]; }
void destroy(int p) { tsh[++tct] = p; }
void clone(int p, int q) {
memcpy(ch[p], ch[q], sizeof ch[0]);
val[p] = val[q];
siz[p] = siz[q];
sum[p] = sum[q];
rev[p] = rev[q];
if (!isleaf(p)) {
use[ch[p][0]] += 1;
use[ch[p][1]] += 1;
}
}
int newnode(LL v) {
int p = tct ? tsh[tct--] : ++tot;
memset(ch[p], 0, sizeof ch[p]);
val[p] = v;
siz[p] = 1;
sum[p] = v;
rev[p] = 0;
use[p] = 1;
return p;
}
void refresh(int &p) {
if (use[p] <= 1) return;
use[p] -= 1;
int q = exchange(p, newnode(0));
clone(p, q);
}
void maintain(int p) { // also known as: pushup
if (isleaf(p)) return;
val[p] = val[ch[p][1]];
sum[p] = sum[ch[p][0]] + sum[ch[p][1]];
siz[p] = siz[ch[p][0]] + siz[ch[p][1]];
}
void spread(int &p) {
if (isleaf(p)) return;
refresh(p);
rev[p] ^= 1;
}
void pushdown(int p) {
if (!rev[p] || isleaf(p)) return;
spread(ch[p][0]), spread(ch[p][1]);
swap(ch[p][0], ch[p][1]);
rev[p] = false;
}
void rotate(int p, int r) {
if (isleaf(p) || isleaf(ch[p][r])) return;
pushdown(ch[p][r]);
refresh(ch[p][r]);
int q = ch[p][r];
swap(ch[p][0], ch[p][1]);
swap(ch[p][r], ch[q][r]);
swap(ch[q][0], ch[q][1]);
maintain(q);
maintain(p);
}
void update(int p) { // also known as: maintain
if (isleaf(p)) return;
int r = siz[ch[p][0]] < siz[ch[p][1]];
if (siz[ch[p][!r]] >= siz[p] * alpha) return;
pushdown(ch[p][r]);
refresh(ch[p][r]);
if (siz[ch[ch[p][r]][!r]] >= siz[ch[p][r]] * (1 - alpha * 2) / (1 - alpha))
rotate(ch[p][r], !r);
rotate(p, r);
}
void insert(int &p, int v, int k) {
pushdown(p);
refresh(p);
int r = siz[ch[p][0]] < k;
if (isleaf(p)) {
ch[p][0] = newnode(val[p]);
ch[p][1] = newnode(v);
} else {
if (r) k -= siz[ch[p][0]];
insert(ch[p][r], v, k);
}
maintain(p);
update(p);
}
void erase(int &p, int k) {
pushdown(p);
refresh(p);
int r = siz[ch[p][0]] < k;
if (isleaf(ch[p][r])) {
// if (val[ch[p][r]] != v) return;
use[ch[p][0]] -= 1;
use[ch[p][1]] -= 1;
clone(p, ch[p][!r]);
} else {
if (r) k -= siz[ch[p][0]];
erase(ch[p][r], k);
}
maintain(p);
update(p);
}
int merge(int p, int q) {
if (!p || !q) return p + q;
if (min(siz[p], siz[q]) >= alpha * (siz[p] + siz[q])) {
int t = newnode(0);
ch[t][0] = p, use[p] += 1;
ch[t][1] = q, use[q] += 1;
maintain(t);
return t;
}
if (siz[p] >= siz[q]) {
pushdown(p);
if (siz[ch[p][0]] >= alpha * (siz[p] + siz[q])) {
return merge(ch[p][0], merge(ch[p][1], q));
} else {
pushdown(ch[p][1]);
return merge(merge(ch[p][0], ch[ch[p][1]][0]),
merge(ch[ch[p][1]][1], q));
}
} else {
pushdown(q);
if (siz[ch[q][1]] >= alpha * (siz[p] + siz[q])) {
return merge(merge(p, ch[q][0]), ch[q][1]);
} else {
pushdown(ch[q][0]);
return merge(merge(p, ch[ch[q][0]][0]),
merge(ch[ch[q][0]][1], ch[q][1]));
}
}
}
void split(int p, int k, int &x, int &y) {
if (!k) return x = 0, y = p, void();
if (isleaf(p)) return x = p, y = 0, void();
pushdown(p);
if (k <= siz[ch[p][0]]) {
split(ch[p][0], k, x, y);
y = merge(y, ch[p][1]);
} else {
split(ch[p][1], k - siz[ch[p][0]], x, y);
x = merge(ch[p][0], x);
}
}
LL getsum(int &p, int k) {
pushdown(p);
int r = siz[ch[p][0]] < k;
if (isleaf(p)) {
return val[p];
} else {
LL ret = 0;
if (r) k -= siz[ch[p][0]], ret += sum[ch[p][0]];
return getsum(ch[p][r], k) + ret;
}
}
LL getsum(int &p, int L, int R) {
auto lans = getsum(p, L);
auto rans = getsum(p, R + 1);
return rans - lans;
}
void dfs(int p, bool r = false) {
r ^= rev[p];
if (isleaf(p)) {
if (val[p] >= -1e9)
debug("%d ", val[p]);
else
debug("-inf ");
} else {
dfs(ch[p][r], r);
dfs(ch[p][!r], r);
}
}
void rem(int p, vector<int> &vec, bool r = false) {
r ^= rev[p];
if (isleaf(p)) {
vec.push_back(val[p]);
} else {
rem(ch[p][r], vec, r);
rem(ch[p][!r], vec, r);
}
}
};
WBLT<5000010> t;
int m;
int root[500010];
int main() {
#ifndef LOCAL
cin.tie(nullptr)->sync_with_stdio(false);
#endif
cin >> m;
root[0] = t.root;
LL lastans = 0;
for (int i = 1; i <= m; i++) {
LL op, l, r;
int v;
cin >> v >> op >> l;
t.use[root[i] = root[v]] += 1;
if (op != 2) cin >> r;
l ^= lastans, r ^= lastans;
int x, y, z;
switch (op) {
case 1:
t.insert(root[i], r, l + 1);
break;
case 2:
t.erase(root[i], l + 1);
break;
case 3:
t.split(root[i], l, x, y);
t.split(y, r - l + 1, y, z);
t.spread(y);
root[i] = t.merge(x, t.merge(y, z));
break;
case 4:
cout << (lastans = t.getsum(root[i], l, r)) << endl;
break;
}
}
return 0;
}
例题:第 \(k\) 小子串
题目描述
定义字典树上的子串为字典树上从上到下的一条有向路径边上所有字符依次连成的字符串,两个字符串 \(S\) 与 \(T\) 本质不同当且仅当 \(|S|\ne|T|\vee(\exists i\in[1,\min(|S|,|T|)],\;S_i\ne T_i)\)。
为了检验单词记忆的成果,你在心里想好了 \(q\) 个问题,每个问题会询问这棵字典树上字典序第 \(k\) 小的本质不同的非空子串。由于这个子串可能会很长,所以你只需要回答整个子串的 \(\textit{ASCII}\) 码之和就可以了。
\(2\leqslant n\leqslant 2\times 10^5,\;1\leqslant q\leqslant 5\times 10^5, k\le 10^{12}\)。
solution
首先对字典树建出广义 SAM,这样,一个子串就是 SAM 的 DAG 上一条从根出发的路径。考虑一些眼前一黑的 dp。设 \(f_u\) 是一个序列,按照字典序记录了所有从 \(u\) 出发的路径。显然 \(f_u\) 有一个暴力转移:
其中 \(\delta(u, r)=v\) 刻画了 DAG,状态 \(u\) 向字符 \(r\) 转移到达状态 \(v\);\((+)\) 是序列拼接,\((\times)\) 表示序列中的每一个路径都前插一个元素,即边代表的字符。
因为这是一个 DAG,考虑使用持久化平衡树优化 \(f\) 的转移,查询时在平衡树上做类似二分的工作。
复杂度是 \(O(n\log n)\)。注意这里因为子串个数显然不超过 \(O(n^2)\),所以平衡树大小不超过 \(O(n^2)\),深度不超过 \(O(\log n^2)=O(\log n)\),这样才能保证复杂度正确。如果这是一般的 DAG,路径数量可以达到 \(O(2^n)\),那么 WBLT 的深度达到 \(O(n)\) 就做不了了。
实际表现上,笔者的持久化 WBLT 的时空都远远不如 \(O(n\log^2n)\) 的 DAG 链剖分。
代码
点击查看代码
#include <bits/stdc++.h>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define debug(...) void(0)
#endif
typedef long long LL;
template <int N>
struct WBLT {
static constexpr double alpha = 0.292;
int ch[N << 1][2], tot, root;
LL siz[N << 1];
int val[N << 1];
int tag[N << 1];
int use[N << 1];
bool isleaf(int p) { return !ch[p][0]; }
void clone(int p, int q) {
memcpy(ch[p], ch[q], sizeof ch[0]);
val[p] = val[q];
siz[p] = siz[q];
tag[p] = tag[q];
if (!isleaf(p)) {
use[ch[p][0]] += 1;
use[ch[p][1]] += 1;
}
}
int newnode(LL v) {
int p = ++tot;
memset(ch[p], 0, sizeof ch[p]);
val[p] = v;
siz[p] = 1;
tag[p] = 0;
use[p] = 1;
return p;
}
void refresh(int &p) {
if (use[p] <= 1) return;
use[p] -= 1;
int q = exchange(p, newnode(0));
clone(p, q);
}
void maintain(int p) { // also known as: pushup
if (isleaf(p)) return;
val[p] = val[ch[p][1]];
siz[p] = siz[ch[p][0]] + siz[ch[p][1]];
}
void spread(int &p, int k) {
refresh(p);
if (!isleaf(p)) tag[p] += k;
val[p] += k;
}
void pushdown(int p) {
if (!tag[p] || isleaf(p)) return;
spread(ch[p][0], tag[p]), spread(ch[p][1], tag[p]);
tag[p] = 0;
}
void rotate(int p, int r) {
if (isleaf(p) || isleaf(ch[p][r])) return;
pushdown(ch[p][r]);
refresh(ch[p][r]);
int q = ch[p][r];
swap(ch[p][0], ch[p][1]);
swap(ch[p][r], ch[q][r]);
swap(ch[q][0], ch[q][1]);
maintain(q);
maintain(p);
}
void update(int p) { // also known as: maintain
if (isleaf(p)) return;
int r = siz[ch[p][0]] < siz[ch[p][1]];
if (siz[ch[p][!r]] >= siz[p] * alpha) return;
pushdown(ch[p][r]);
refresh(ch[p][r]);
if (siz[ch[ch[p][r]][!r]] >= siz[ch[p][r]] * (1 - alpha * 2) / (1 - alpha))
rotate(ch[p][r], !r);
rotate(p, r);
}
void insert(int &p, int v, int k) {
pushdown(p);
refresh(p);
int r = siz[ch[p][0]] < k;
if (isleaf(p)) {
ch[p][0] = newnode(val[p]);
ch[p][1] = newnode(v);
} else {
if (r) k -= siz[ch[p][0]];
insert(ch[p][r], v, k);
}
maintain(p);
update(p);
}
void erase(int &p, int k) {
pushdown(p);
refresh(p);
int r = siz[ch[p][0]] < k;
if (isleaf(ch[p][r])) {
// if (val[ch[p][r]] != v) return;
use[ch[p][0]] -= 1;
use[ch[p][1]] -= 1;
clone(p, ch[p][!r]);
} else {
if (r) k -= siz[ch[p][0]];
erase(ch[p][r], k);
}
maintain(p);
update(p);
}
int merge(int p, int q) {
if (!p || !q) return p + q;
if (min(siz[p], siz[q]) >= alpha * (siz[p] + siz[q])) {
int t = newnode(0);
ch[t][0] = p, use[p] += 1;
ch[t][1] = q, use[q] += 1;
maintain(t);
return t;
}
if (siz[p] >= siz[q]) {
pushdown(p);
if (siz[ch[p][0]] >= alpha * (siz[p] + siz[q])) {
return merge(ch[p][0], merge(ch[p][1], q));
} else {
pushdown(ch[p][1]);
return merge(merge(ch[p][0], ch[ch[p][1]][0]),
merge(ch[ch[p][1]][1], q));
}
} else {
pushdown(q);
if (siz[ch[q][1]] >= alpha * (siz[p] + siz[q])) {
return merge(merge(p, ch[q][0]), ch[q][1]);
} else {
pushdown(ch[q][0]);
return merge(merge(p, ch[ch[q][0]][0]),
merge(ch[ch[q][0]][1], ch[q][1]));
}
}
}
void split(int p, int k, int &x, int &y) {
if (!k) return x = 0, y = p, void();
if (isleaf(p)) return x = p, y = 0, void();
pushdown(p);
if (k <= siz[ch[p][0]]) {
split(ch[p][0], k, x, y);
y = merge(y, ch[p][1]);
} else {
split(ch[p][1], k - siz[ch[p][0]], x, y);
x = merge(ch[p][0], x);
}
}
int query(int p, LL k, int pre = 0) {
int r = siz[ch[p][0]] < k;
if (isleaf(p))
return val[p] + pre;
else
return r && (k -= siz[ch[p][0]]), query(ch[p][r], k, pre + tag[p]);
}
};
template <int N, int M>
struct suffixam {
int ch[N << 1][M], tot, len[N << 1], link[N << 1];
suffixam() : tot(1) {
memset(ch[1], 0, sizeof ch[0]);
link[1] = len[1] = 0;
}
int split(int p, int q, int r) {
if (len[q] == len[p] + 1) return q;
int u = ++tot;
len[u] = len[p] + 1;
memcpy(ch[u], ch[q], sizeof ch[0]);
link[u] = link[q], link[q] = u;
for (; p && ch[p][r] == q; p = link[p]) ch[p][r] = u;
return u;
}
int expand(int p, int r) {
if (ch[p][r]) return split(p, ch[p][r], r);
int u = ++tot;
len[u] = len[p] + 1;
memset(ch[u], 0, sizeof ch[0]);
for (; p; p = link[p]) {
if (!ch[p][r])
ch[p][r] = u;
else
return link[u] = split(p, ch[p][r], r), u;
}
return link[u] = 1, u;
}
};
int n, m, Q;
suffixam<1 << 18, 26> s;
vector<pair<int, int>> g[1 << 18];
void bfs() {
queue<tuple<int, int, int>> q;
q.emplace(1, 0, 1);
while (!q.empty()) {
int u, fa, last;
tie(u, fa, last) = q.front();
q.pop();
for (auto e : g[u])
if (e.first != fa) {
int v = e.first, r = e.second;
q.emplace(v, u, s.expand(last, r));
}
}
}
int per[1 << 19], root[1 << 19];
void toposort() {
static int buc[1 << 19];
memset(buc, 0, sizeof buc);
for (int i = 1; i <= m; i++) ++buc[s.len[i]];
for (int i = 1; i <= m; i++) buc[i] += buc[i - 1];
for (int i = m; i >= 1; i--) per[buc[s.len[i]]--] = i;
}
WBLT<400010 << 5> t;
int main() {
#ifndef LOCAL
freopen("gre.in", "r", stdin);
freopen("gre.out", "w", stdout);
#endif
scanf("%d%d", &n, &Q);
for (int i = 1; i < n; i++) {
int u, v;
char ch;
scanf("%d%d %c", &u, &v, &ch);
g[u].emplace_back(v, ch - 'a');
g[v].emplace_back(u, ch - 'a');
}
bfs();
m = s.tot;
toposort();
for (int j = m; j >= 1; j--) {
int p = per[j];
root[p] = t.newnode(0);
for (int r = 0; r < 26; r++)
if (s.ch[p][r]) {
int q = t.newnode(0);
t.clone(q, root[s.ch[p][r]]);
t.spread(q, r + 'a');
root[p] = t.merge(root[p], q);
}
}
debug("There are %lld paths.\n", t.siz[root[1]]);
for (LL k; Q--;
scanf("%lld", &k),
printf("%lld\n", ++k <= t.siz[root[1]] ? t.query(root[1], k) : -1ll))
;
return 0;
}
例题:区间复制
给一个序列,\(m\) 次操作支持 \(\forall l_1\leq i\leq r_1, a_i\gets a_{i - l_1 + l_2}\)。\(n, m\leq 10^5\),\([l_1, r_1]\cap[l_2, r_2]=\varnothing\)。
考虑分裂出 \([l_1, l_2], [l_2, r_2]\) 后,把 \([l_2, r_2]\) 那个部分拼两次到序列中,使用持久化平衡树维护,\(O(m\log n)\)。
但这样有个问题就是你的空间有点太极端了。考虑每做 \(O(n/\log n)\) 次操作后,增加了 \(O(n/\log n)\times O(\log n)=O(n)\) 的空间,然后我们把序列拿出来,全部重构一遍,所有的节点都回炉重造,重新开始。重构的复杂度和空间复杂度一样,一共进行了 \(O(m\log n/n)\) 次重构,每一次重构 \(O(n)\),重构代价是 \(O(m\log n)\),不影响时间复杂度,却把空间复杂度降至 \(O(n)\)。
笔者没有实现这个代码,因此没有代码。
本文来自博客园,作者:caijianhong,转载请注明原文链接:https://www.cnblogs.com/caijianhong/p/17999815/template-wblt


 浙公网安备 33010602011771号
浙公网安备 33010602011771号