题解 AtCoder wtf22_day1_b【Non-Overlapping Swaps】

题解 AtCoder wtf22_day1_b【Non-Overlapping Swaps】

problem

给定一个排列，要求交换最多 \(n-1\) 对元素，使得这个排列变成 [1,2,...,n] 的有序排列。

当然没有那么简单，对于交换还是有限制的，对于相邻的两次交换，不妨叫做 \((l_i, r_i)\) 和 \((l_{i+1}, r_{i+1})\)，必须满足这两个交换所对应的区间，没有交集，即：

• 要么 \(r_i <= l_{i+1}\)；
• 要么 \(r_{i+1} <= l_i\)。

请给出一种构造。

\(n\leq 200000\)。

solution

考虑对于一个置换环，如果能解决一个置换环的问题，那么在两个置换环中间插入 1 1 就能将两个置换环连接起来。所以我们只需要考虑一个置换环。

考虑一个置换环，我们连边 \(i\to p_i\)，然后取出标号最小的两个元素，不妨记为 \(a,b\)。考虑构造：

• 首先找到 \(a\) 的前驱，记为 \(c\)，使 \(c\) 重新连向 \(b\)，对 \(c\to b\) 所在的置换环（绿色）进行递归构造。
• 然后交换 \(a,b\)。（浅蓝色）
• 找到之前 \(a\) 的后继，记为 \(d\)，将 \(a\)（现在在原来 \(b\) 的位置）重新连向 \(d\)，对 \(a\to d\) 所在的置换环（棕色）进行递归构造。

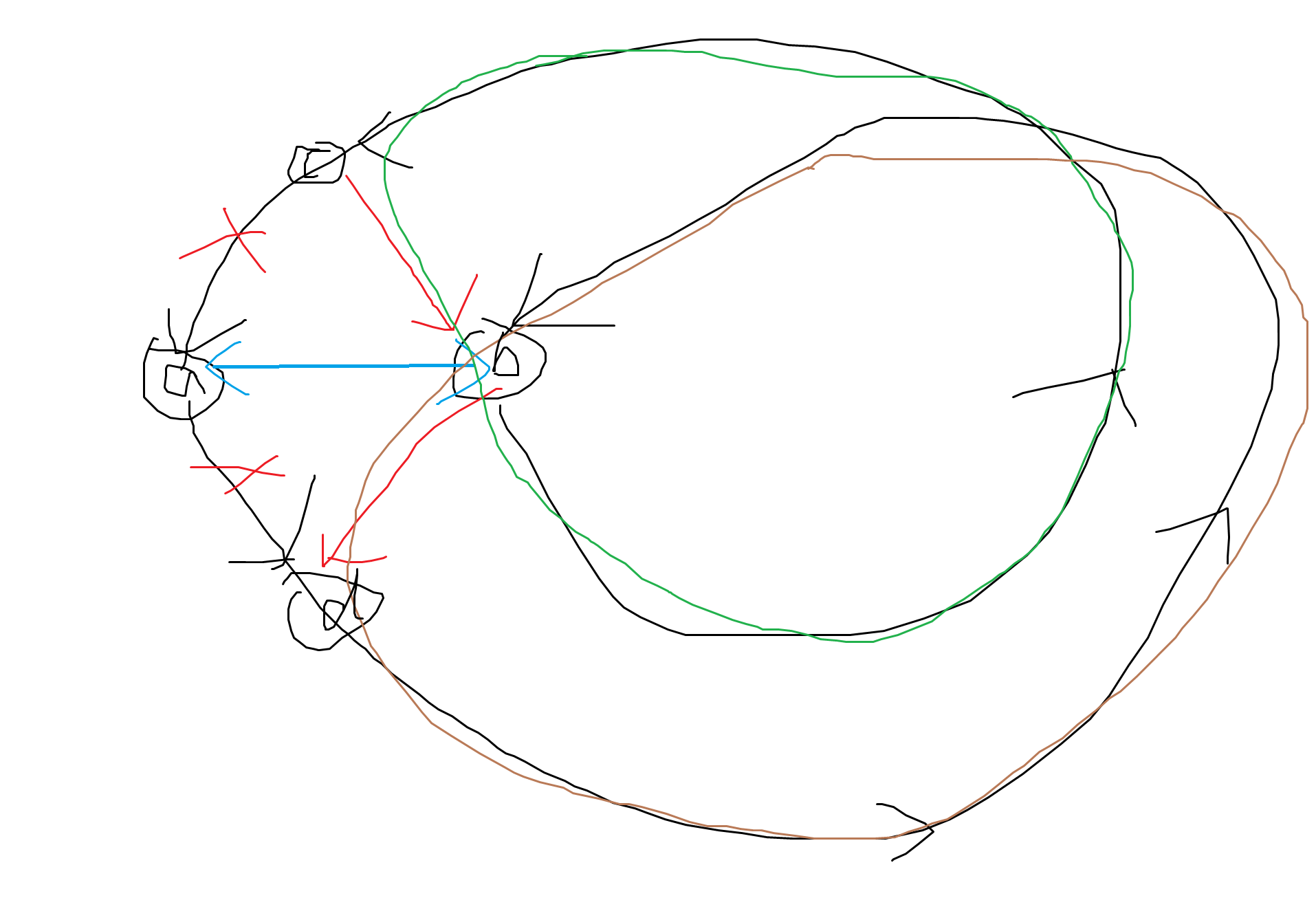
正确性：

• 不是 \(a,b,c,d\) 的点，都被交换到它的后继。
• \(a\) 确实最后到达了 \(d\) 的位置，\(b\) 到达了 \(b\) 的后继，\(d\) 到达了 \(d\) 的后继，\(c\) 到达了 \(b\) 原来所有的位置后被 swap 到原来 \(a\) 的位置。
• （这个题的位置关系很乱，本文统一使用“前驱” “后继”）
• 做完绿色置换环后，交换 \(a, b\)，不会产生冲突，因为根据定义，\(a,b\) 是标号最小的。如果冲突了说明其中有一个点的标号 \(<b\)。
• 同理，交换 \(a, b\) 后做棕色置换环，不会产生冲突。

那么这是一个合法的构造，我们如果要实现这个过程有两种方法：

method 1

用一个 std::set 表示这个置换环，则我们可以轻易找出这个置换环的标号最小的两个节点。然后我们发现不能轻易地分裂两个置换环，因为时间复杂度会爆炸。考虑启发式分裂，每次将小的分裂出去；找到小的置换环，只需要使用两个指针在两个置换环上分别跳，谁先回到原点谁就是小置换环；这样判断的复杂度是 \(O(2siz_{small})\) 因此非常正确，然后在 set 中删数也是非常正确，一共 \(O(n\log^2n)\)。

method 2

考虑所谓拿出最小值的过程可以类比笛卡尔树，于是我们的惊人结论是将置换环拍成一行后，将最小的放在前面，然后建笛卡尔树。使用笛卡尔树构造方案，先递归左子树，然后交换它与父亲，然后递归右子树。这样就完美实现题目过程（最小的点相当于父亲，而次小相当于儿子，类似这样）。\(O(n)\)。至于为什么最小的要放在前面，因为最小的点作为树根，没有父亲提供中转。

code

//505161648
#include <cstdio>
#include <vector>
#include <cstring>
#include <cassert>
#include <algorithm>
using namespace std;
#ifdef LOCAL
#define debug(...) fprintf(stderr, ##__VA_ARGS__)
#else
#define debug(...) void(0)
#endif
typedef long long LL;
int n, a[1 << 18], vis[1 << 18], tim, ch[1 << 18][2];
int build(vector<int> h) {
    static int stk[1 << 18];
    int top = 0; ch[0][1] = stk[++top] = h[0];
    for (int p: h) {
        ch[p][0] = ch[p][1] = 0;
        if (p == h[0]) continue;
        while (top && stk[top] >= p) --top;
        ch[p][0] = ch[stk[top]][1];
        ch[stk[top]][1] = p;
        stk[++top] = p;
    }
    return ch[0][1];
}
void dfs(int p, int f) {
    if (!p) return ;
    dfs(ch[p][0], p);
    if (f) {
        int l = p, r = f;
        if (l > r) swap(l, r);
        printf("%d %d\n", l, r);
    }
    dfs(ch[p][1], p);
}
int mian() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
    printf("%d\n", n - 1);
    int last = 0;
    for (int i = 1; i <= n; i++) if (vis[i] < tim) {
        vector<int> h;
        for (int p = i; vis[p] < tim; p = a[p]) h.push_back(p), vis[p] = tim;
        reverse(h.begin(), h.end());
        rotate(h.begin(), prev(h.end()) ,h.end());
        if (last) printf("1 1\n");
        else last = i;
        dfs(build(h), 0);
    }
    return 0;
}
int main() {
    int T;
    scanf("%d", &T);
    while (T--) ++tim, mian();
    return 0;
}