【笔记】简单解析几何(OI 无关)
首先我不太清楚什么是解析几何什么是计算几何,总之在这里它指在平面内的一些计算。
向量
见 题解 HDU3629【Convex】—— prework:向量。内容很少。
向量运算的性质定理
以下是一些小性质,或者叫定义,我不知道:
- \(\vec a\times\vec b=X_aY_b-X_bY_a\)。(叉乘的本质是二维行列式)
- 平行判定:\(a//b\Leftrightarrow\vec a\times \vec b=0\)。
- 垂直判定:\(a\perp b\Leftrightarrow\vec a\cdot \vec b=0\)。
- 模长:\(|a|=\sqrt{x^2+y^2}=\sqrt{a\cdot a}\)。
- 辐角:\(\theta=\arctan \frac{y}{x}\)。
当然我们这是数学不是 OI,所以以下我们暂时不管过程啊。要写过程就怎么呢,过点 A 作 \(x\) 轴、\(y\) 轴的垂线,云云,不管。
一次函数
\(y=kx+b\) 这种一次函数怎么搞?我们叫 \(k\) 为斜率,\(b\) 为截距(与 \(y\) 轴交点的 \(y\) 坐标)。
- 过两点插直线:求 \(k=\frac{y_2-y_1}{x_2-x_1}\),然后它可以写成 \(y-y_1=k(x-x_1)\) 并化简它。千万不要待定系数法,太慢了。
- 两直线求交:联立两个直线方程。
- 两直线平行判定:斜率相同。
- 两直线垂直判定:斜率的乘积为 \(-1\)。
垂直平分线
中点公式:\((\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})\)。
首先求中点,然后这条线的斜率是已知的,然后插就是了。
点到直线的距离
直线 \(l:Ax+By+C=0\),点 \(P(x_0,y_0)\),则点 \(P\) 到直线 \(l\) 的距离为:
因为 \(y=kx+b\Rightarrow kx-y+b=0\),所以也写作
三角函数
就是三角函数的东西,见 题解 HDU3629【Convex】—— prework:三角函数初步。内容很少。
另外有 \(\cot x=\dfrac 1 {\tan x}, \csc x = \dfrac 1 {\sin x}, \sec x = \dfrac 1 {\cos x}\)
和积化差
主要是这两个公式:
- \(\sin(\alpha\pm\beta)=\sin\alpha\cos\beta\pm\cos\alpha\sin\beta\)
- \(\cos(\alpha\pm\beta)=\cos\alpha\cos\beta\mp\sin\alpha\sin\beta\)
\(\begin{bmatrix}\sin,\cos\\\cos,-\sin\end{bmatrix}\alpha+\begin{bmatrix}\cos,\sin\\\cos,\sin\end{bmatrix}\beta\)
其它都可以推,都可以推。
推一下:
再推就是 \(\tan(\alpha\pm\beta)=\frac{\tan\alpha\pm\tan\beta}{1\mp\tan\alpha\tan\beta}\)。这里为后文埋下伏笔(那还叫伏笔?)
诱导
| \(\alpha\) | \(\sin\) | \(\cos\) | \(\tan\) |
|---|---|---|---|
| \(2\pi+\alpha\) | \(\sin\) | \(\cos\) | \(\tan\) |
| \(2\pi-\alpha\) | \(-\sin\) | \(\cos\) | \(-\tan\) |
| \(\pi+\alpha\) | \(-\sin\) | \(-\cos\) | \(\tan\) |
| \(\pi-\alpha\) | \(\sin\) | \(-\cos\) | \(-\tan\) |
| \(\pi/2+\alpha\) | \(\cos\) | \(-\sin\) | \(-\tan^{-1}\) |
| \(\pi/2-\alpha\) | \(\cos\) | \(\sin\) | \(\tan^{-1}\) |
| \(3\pi/2+\alpha\) | \(-\cos\) | \(\sin\) | \(-\tan^{-1}\) |
| \(3\pi/2-\alpha\) | \(-\cos\) | \(-\sin\) | \(\tan^{-1}\) |
看的方法:如 \(\cos(\pi/2+\alpha)=-\sin\alpha\)(交错组合)
特殊角
- \(0,2\pi=360^\circ\) 对应 \((1,0)\) 这个点。
- \(\pi/2=90^\circ\) 对应 \((0,1)\) 这个点。
- \(\pi=180^\circ\) 对应 \((-1,0)\) 这个点。
- \(3\pi/2=270^\circ\) 对应 \((0,-1)\) 这个点。
- \(\pi/6=30^\circ\) 对应的是 \((\frac{\sqrt{3}}{2},\frac{1}{2})\)。等边三角形。
- \(\pi/4=45^\circ\) 对应的是 \((\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})\)。
余弦定理
\(a^2=b^2+c^2-2bc\cos A\)
正弦定理
\(\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2r\),\(r\) 是外接圆半径。
你发现有了这两个定理,给出 SSS(余弦),SAS(余弦),AAS(正弦),ASA(正弦) 的三角形,从理论上来说都可以解三角形。
三角形的面积
\(\Delta ABC\),则 \(S=|\frac{1}{2}(\vec{AB}\times\vec{AC})|\)。
平行四边形
平行四边形 \(ABCD\)(已经有顺序了),判定的原则是:\(\vec{AD}=\vec{BC}\),或者反过来,就是平行且相等。
这里我们思考一个问题:已知点 \(A,B,C\),求剩下一个点 \(D\) 使它们组成平行四边形的方案数。一共六种,\(3\) 个重根,剩下的分别是:
- \(A+\vec{BC}\)
- \(B+\vec{CA}\)
- \(C+\vec{AB}\)
等腰三角形
判定就是 \(AB=AC\),没有别的很好的办法了。
但是一个好玩的:已知点 \(A,B\),求点 \(C\) 使得 \(\Delta ABC\) 为等腰三角形,我们欣赏一下:
那些线都是
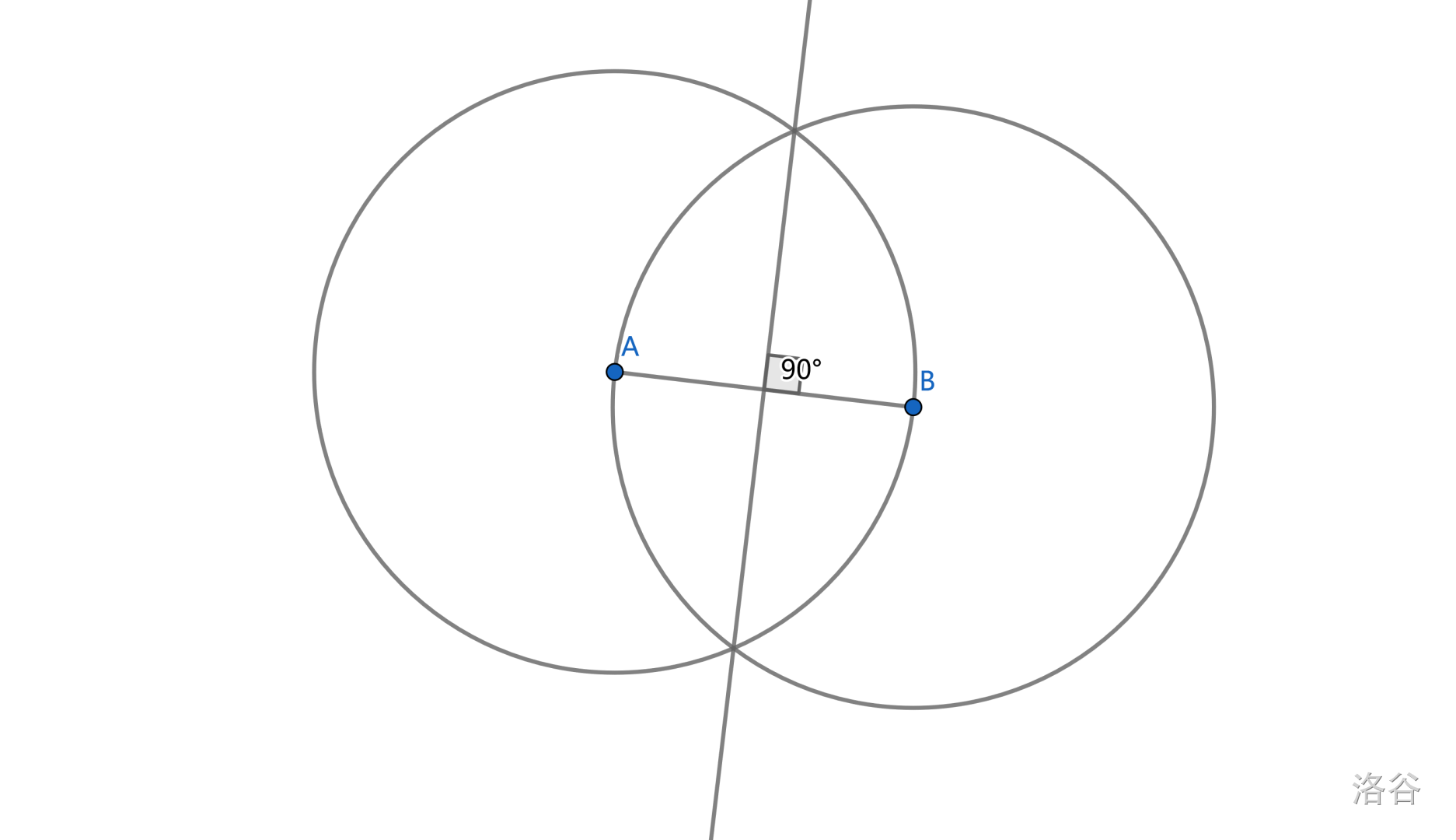
所以如果问方案数的,你画一次这个图,然后用一条直线截它就行了。
直角三角形
勾股定理:\(\angle C=90^\circ\Leftrightarrow AC^2+BC^2=AB^2\)。
但是一个好玩的:已知点 \(A,B\),求点 \(C\) 使得 \(\Delta ABC\) 为直角三角形,我们欣赏一下:
好玩的图像
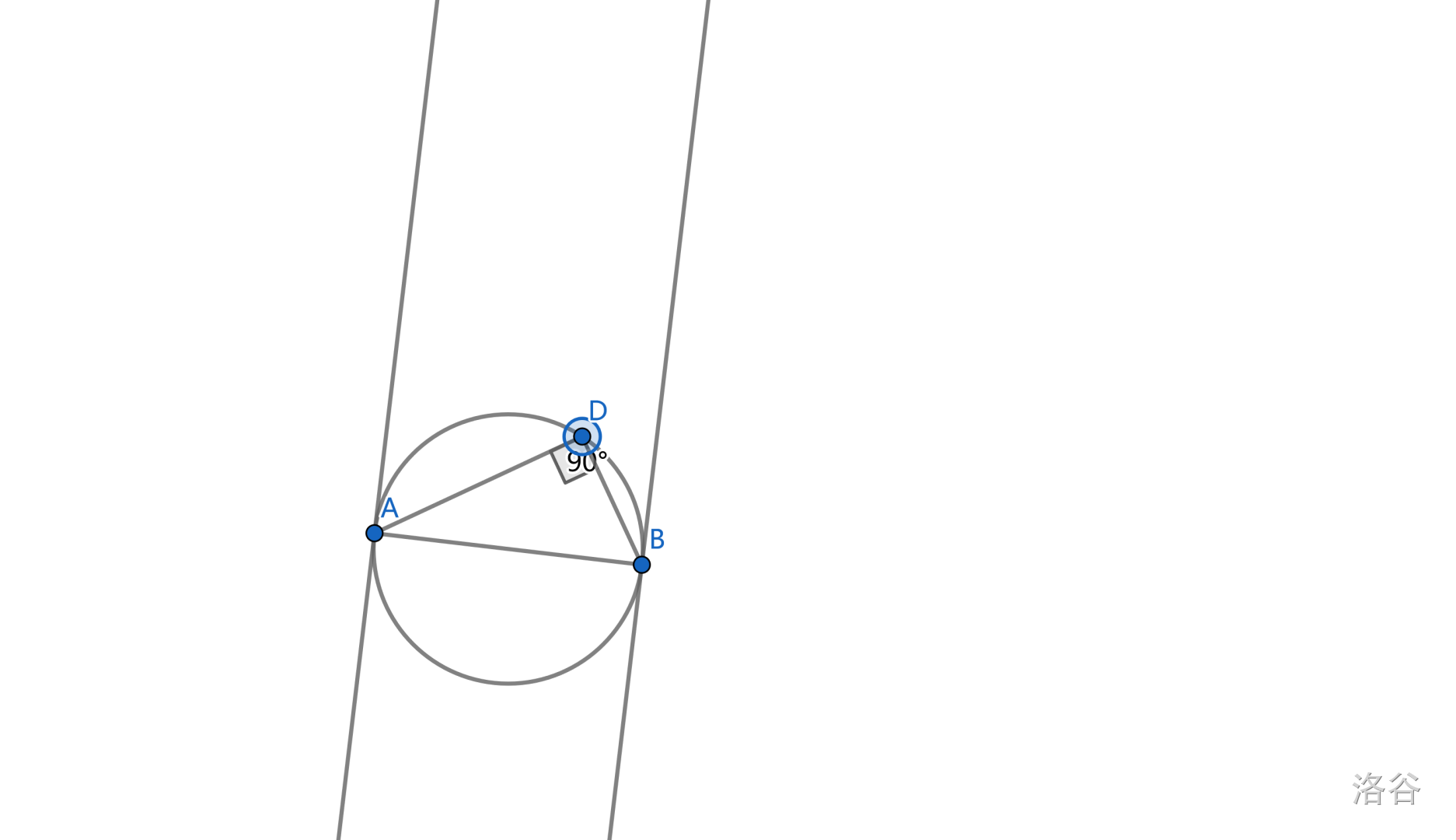
等腰直角三角形
法一
等腰 \(Rt\Delta ABC\),其中 \(\angle B=90^\circ\),它的判定是什么?
- \(|\vec{AB}|=|\vec{BC}|\)
- \(AB\perp BC\)
我们仔细思考一下会发现:其实是 \(\vec{BA}=(x_1,y_1)\) 和 \(\vec{BC}=(x_2,y_2)\),然后 \(x_1=y_2,x_2+y_1=0\) 或 \(x_2=y_1,x_1+y_2=0\)。证明是感性理解。
这是暴力做法,纯正几何做法是一线三垂直。但都搞到这份上了,就不管过程之类的了。
法二
注意到等腰直角三角形的一个角是 \(45^\circ=\pi/4\),有的题目就会问你,一条直线旋转 \(\pi/4\) 之后与另一条直线的交点是什么,这种的几何做法还是一线三等角,但我们可以给它进行降维打击:
注意到 \(\sin\pi/4=\cos\pi/4=\sqrt{2}/2\)(什么你问我怎么证?考虑 \(\sin^2+\cos^2=1\))。所以 \(\tan\pi/4=1\)。
令要旋转直线的斜率是 \(k\),我们要求的新直线的斜率是(以逆时针为例,顺时针取负倒数):
所以是降维打击。
你能解释为什么对于函数 \(f(x)=\frac{1+x}{1-x}\),总有 \(f(f(f(f(x))))=x\) 了吗?什么时候会出现除以 \(0\)?
法三
三个点 \(A,B,C\),如果 \(AB\) 很好求,点 \(C\) 到 \(AB\) 的距离很好求(有时表现为点 \(C\) 在坐标轴上且 \(AB\) 平行于那条坐标轴),我们叫做 \(h\)。
那么分讨很少:
- \(AB=h\)。这是 \(AB\) 为一条腰的情况。
- \(AB=2h\)。这是 \(AB\) 为底的情况。
等腰三角形“三线合一”:等腰三角形中,底边的中线、顶角的角平分线、底边上的高,互相重合。
在直角三角形中,斜边上的中线等于斜边的一半。
于是可以很快乐的求出点 \(A,B\),至于 \(C\),如果是第一种情况就注意一下两边都有可能做垂线,第二种情况就做 \(AB\) 的垂直平分线之类的东西。
暂时写到这里,去写作业。
本文来自博客园,作者:caijianhong,转载请注明原文链接:https://www.cnblogs.com/caijianhong/p/16999127.html


