【笔记】动态规划：斜率优化、WQS 二分

posted on 2022-07-26 15:03:06 | under 学术 | source

太难所以要写，我太菜了。

斜率优化

problem

形如

\[f_i=\min/\max\limits_{1\leq j<i}\{{f_j-a_i\cdot c_j}\}+d_i \]

的式子可以被斜率优化。它的特征是，拥有一个关于 \(i,j\) 的项。

solution

为了优化它，考虑写成直线方程，我们可以移项：

\[f_i-d_i+a_i\cdot c_j=f_j \]

令 \(b=f_i-d_i,k=a_i,x=c_j,y=f_j\)，则 \(b+kx=y\)，原问题转化成：

初始时平面上没有点，需要支持操作：

• 插入一个点 \((x,y)\)。实际操作时插入 \((c_j,f_j)\)。
• 给定斜率 \(k=a_i\)，找到一条过平面上任意一点的直线，使截距 \(b=f_i-d_i\) 最小。

这是线性规划问题，维护一个凸包。如果询问 \(\min\) 维护下凸包，否则上凸包（或者想象是 \(y=\infty\) 有用（上）还是 \(y=-\infty\) 有用（下））。如果插入的 \(x=c_j\) 和询问的 \(k=a_i\) 单调，使用单调队列维护 \(O(n)\)；如果询问的 \(k=a_i\) 不单调，在单调栈上二分 \(O(n\log n)\)；如果插入的 \(x=c_j\) 和询问的 \(k=a_i\) 不单调，使用平衡树（std::set）或李超线段树维护凸包 \(O(n\log n)\)。

来自 2023 年：斜率优化就是将决策点表示成 \((x_j,y_j)\) 的形式，然后转移 \(i\) 时用一个固定的斜率 \(k_i\) 去切这些点，使切得的截距 \(b=y_j-k_ix_j\) 最小/最大。可以通过维护凸包的方式解决。

pre-knowledge

为了写程序方便，引入向量 \(\vec{a}=(x,y)\)。\(\vec{a}\) 本质上是一个点的偏移量，因此我们不关心它的起点是什么，可以减，例如两个点 \(A=(x_1,y_1),B=(x_2,y_2)\)，有向线段可以表示为向量 \(\vec{AB}=(x_2-x_1,y_2-y_1)\)。注意到令 \(O=(0,0)\) 为原点，\(\vec{OA}=(x,y)=A\) 因此向量可以用点的方式存储。

令 \(\vec{a}=(x_1,y_1),\vec{b}=(x_2,y_2)\)，定义一些运算：

• 向量模长：\(|\vec{a}|=\sqrt{x^2+y^2}\).
• 向量加法：\(\vec{a}+\vec{b}=(x_1+x_2,y_1+y_2)\)。
• 向量减法：\(\vec{a}-\vec{b}=(x_1-x_2,y_1-y_2)\)。
• 向量数乘：\(\lambda\vec{a}=(\lambda x,\lambda y)\)。
• 向量点乘：\(\vec{a}\cdot\vec{b}=x_1x_2+y_1y_2\)。
• 向量叉乘：\(\vec{a}\times\vec{b}=x_1y_2-x_2y_1\)。

template<class T=double> struct dot{
	T x,y;
	dot(T x=0,T y=0):x(x),y(y){}
	dot operator+(dot b){return dot(x+b.x,y+b.y);}
	dot operator-(dot b){return dot(x-b.x,y-b.y);}
	dot operator*(T k){return dot(x*k,y*k);}
	T operator*(dot b){return x*b.y-b.x*y;}
	T operator^(dot b){return x*b.x+y*b.y;}
	friend T dist(dot a){return sqrt(a^a);}
};

点乘和叉乘都属于乘法，书写的时候给它们钦定一个符号，例如下文规定 \(\vec{a}\times{\vec{b}}\) 是叉乘。叉乘拥有很重要的性质，首先它没有交换律，结果可正可负可 \(0\)，其次 \(\vec{a}\times{\vec{b}}\) 表示 \(\vec{a}\) 逆时针（不超过 \(180^\circ\)）转到 \(\vec{b}\) 扫过的（平行四边形的）面积。注意到向量的起点不重要，可以把两个向量放在一起转（具体地，通过平移，两个平行向量叉积为 \(0\)）。那我们考虑怎么用叉乘维护凸包呢？

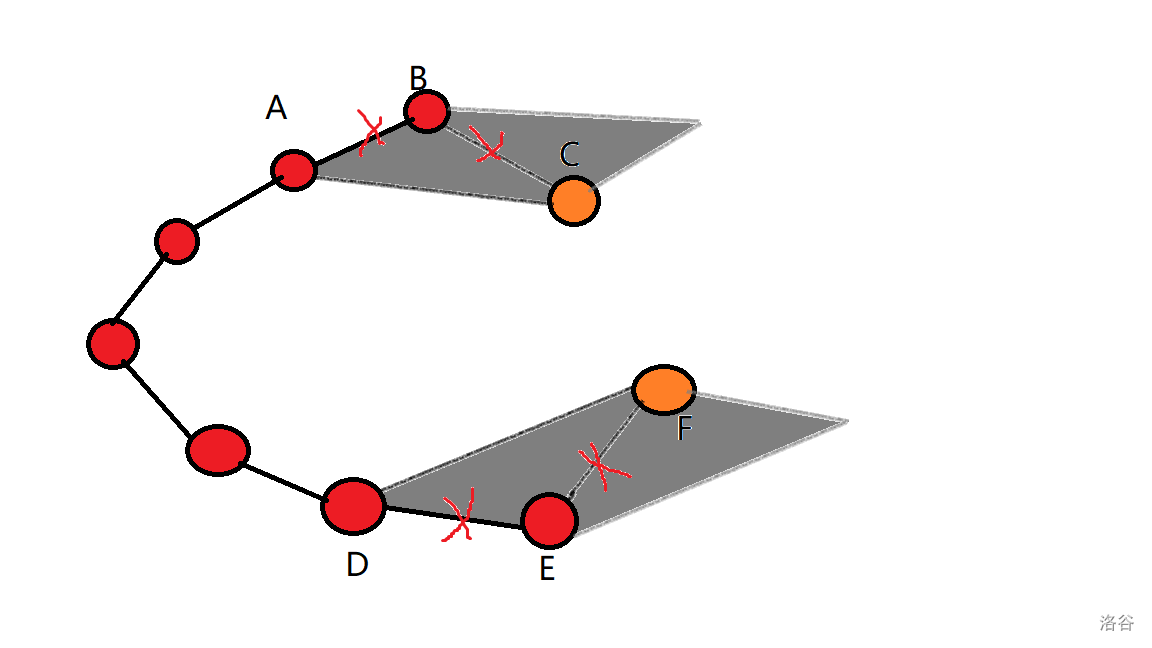
这是一个凸包，我们将其分裂成上凸包和下凸包。观察下凸包，我们将加入点 \(F\)，如果 \(\vec{DE}\times\vec{DF}\geq 0\)，说明这个平行四边形（阴影部分）存在，这肯定不是下凸包了，于是将点 \(E\) 弃掉。观察上凸包，我们将加入点 \(C\)，如果 \(\vec{AC}\times\vec{AB}\geq 0\) 就把点 \(B\) 弃掉。我们成功的维护了一个凸包。

那么怎么在凸包上二分斜率呢？一模一样，考虑对于斜率 \(k\)，固定起点为 \(O\)，则这个向量可以被表示为 \((1,k)\)，这是斜率的定义。然后画个图把这个向量和队首两个点组成的有向线段求叉积，看一下 \(>0\) 还是 \(<0\)，注意 \(=0\) 的是合法答案不要干掉。

example：P5785 [SDOI2012]任务安排

优化下列递推过程，其中 \(sc_i\) 单调不降，\(n\leq 3\times 10^5\)。

\[f_i=\min\limits_{1\leq j<i}\{f_j+st_i(sc_i-sc_j)+S(sc_n-sc_j)\} \]

解：忽略 \(\min\)，考虑拆开括号并移项：

\[f_i=f_j+st_isc_i-st_isc_j+Ssc_n-Ssc_j \]

\[\boxed{f_i-st_isc_i-Ssc_n}=\boxed{f_j-Ssc_j}-\boxed{st_isc_j} \]

熟悉的样子，令 \(b=f_i-st_isc_i-Ssc_n,y=f_j-Ssc_j,k=st_i,x=sc_j\)。于是可以斜率优化。注意到我们其实不太关心 \(b\) 是什么。

typedef long long LL;
int n,s;
dot<LL> q[300010];
LL sc[300010],st[300010],f[300010];
dot<LL> binary(int L,int R,dot<LL> p){
	int ans=R+1;
	while(L<=R){
		int mid=(L+R)>>1;
		if((q[mid+1]-q[mid])*p>0) L=mid+1;
		else R=mid-1,ans=mid;
	}
	return q[ans];
}
LL dp(){
	int L=1,R=0;q[++R]=dot<LL>(0,0);
	for(int i=1;i<=n;i++){
//		while(L<R&&(q[L+1]-q[L])*dot<LL>(1,st[i])>0) L++; 保证st单调可以单调队列
		//注意到凸包的线段斜率单调
		dot<LL> pre=binary(1,R-1,dot<LL>(1,st[i]));//否则在单调栈上二分
		f[i]=pre.y-st[i]*pre.x+st[i]*sc[i]+sc[n]*s;
		dot<LL> p=dot<LL>(sc[i],f[i]-s*sc[i]);
		while(L<R&&(p-q[R-1])*(q[R]-q[R-1])>=0) R--;
		q[++R]=p;
	}
	return f[n];
}

凸优化/WQS 二分

problem

有 \(n\) 个物品，求恰好选 \(k\) 个得到的最小权值。令 \(g(x)\) 为恰好选 \(x\) 个物品的最小权值，如果 \(\bold{g(x)}\) 是凸函数，则可以使用凸优化。

solution

解：二分一个 \(C\)，表示选一次物品要加上 \(C\) 的代价，若 \(C\) 越大能选的物品更少（因题而异），则若选的物品数量 \(\leq k\) 时，增大 \(C\)，否则减少 \(C\)。

这个做法有一些边界问题：我们可能二分出一个 \(g(l)=C,g(r)=C+1\)，然后发现 \(l<k<r\)，答案竟然在线段上，一般的解决方法是强行认为选了 \(k\) 个物品，最后必须减掉 \(k\) 个物品的贡献。

时间复杂度：\(O(\log nf(n))\)，其中 \(f(n)\) 是 check 一次的时间。我们用 \(\log n\) 换掉了 \(n\)。

explanation

我们枚举的 \(C\) 事实上是一个斜率，考虑在平面上对于每一个 \(i\in [1,n]\) 有一个 \((i,g(i))\) 的点，则这些点形成一个凸包。以上凸包为例，由于 \(g(m)\) 一般很难求出，我们考虑用一条斜率为 \(k\) 的直线切这个凸包。和斜率优化相似，我们假设这条直线是 \(y-kx=b\)，令 \(b=f(x)\)，试图算出 \(f(x)\)，由定义得 \(g(x)=f(x)-kx\)，于是我每选一个点就把贡献加上 \(k\)，最后减掉，于是我们算出了 \(x,g(x)\)，拿着这个 \(x,g(x)\) 二分答案即可。

example：P2619 [国家集训队]Tree I

求恰好选 \(k\) 条白边的最小生成树。

注意在排序上动点手脚，先选白边，最后算答案强行认为选了 \(k\) 条白边。

bool operator<(edge b){return w.first==b.w.first?w.second>b.w.second:w.first<b.w.first;}
int n,m,k;
graph<50010,100010,node> g;
node check(int d){
	dsu<50010> s(n);
	for(int i=1;i<=g.cnt;i++) g[i].w.first+=g[i].w.second*d;
	sort(g.e+1,g.e+g.cnt+1);
	node res=node(0,0);
	for(int i=1;i<=g.cnt;i++){
		int u=g[i].u,v=g[i].v;
		if(s.find(u)!=s.find(v)){
			s.merge(u,v);
			res.first+=g[i].w.first;
			res.second+=g[i].w.second;
		}
	}
	for(int i=1;i<=g.cnt;i++) g[i].w.first-=g[i].w.second*d;
	return res;
}
int binary(int L,int R){
	int ans=-1e9;
	while(L<=R){
		int mid=(L+R)>>1;
		node res=check(mid);
		if(res.second>=k) ans=res.first-k*mid,L=mid+1;
        //								^
		else R=mid-1;
	}
	return ans;
}
int main(){
	scanf("%d%d%d",&n,&m,&k);
	for(int i=1,u,v,w,z;i<=m;i++) scanf("%d%d%d%d",&u,&v,&w,&z),g.add(u+1,v+1,node(w,!z));
	printf("%d\n",binary(-114,114));
	return 0;
}