【模板】广义后缀自动机 exSAM

posted on 2022-11-02 18:51:48 | under 模板 | source

link -> https://www.cnblogs.com/caijianhong/p/template-suffixam.html

重要结论：反串上跳 fail 等价于正串上跳 next。

点击查看代码

template<int N,int M> struct suffixam{
	int ch[N<<1][M],link[N<<1],len[N<<1],tot;
	suffixam():tot(1){link[1]=0,len[1]=0;}
	int split(int r,int p,int q){
		if(len[q]==len[p]+1) return q;
		int u=++tot; len[u]=len[p]+1;
		memcpy(ch[u],ch[q],sizeof ch[0]);
		link[u]=link[q],link[q]=u;
		for(;p&&ch[p][r]==q;p=link[p]) ch[p][r]=u;
		return u;
	}
	int expand(int r,int p){
		if(ch[p][r]) return split(r,p,ch[p][r]);
		int u=++tot; len[u]=len[p]+1;
		for(;p;p=link[p]){
			if(ch[p][r]) return link[u]=split(r,p,ch[p][r]),u;
			else ch[p][r]=u;
		}
		return link[u]=1,u;
	}
};

solution

膜拜 @xzzduang。

我们重学一个 SAM。

一个点维护的是所有 \(endpos=S\) 的（本质不同的）串，显然这些串的长度连续，较短者为最长者的后缀，我们记最长的长度为 \(len_u\)。

从根节点出发，到达点 \(u\) 的所有路径组成的字符串就是点 \(u\) 维护的字符串。

什么是转移边 / 出边 \(ch_{u,i}\)？表示在点 \(u\) 维护的字符串等价类后面加上字符 \(a\)。

什么是后缀链接 \(link_u\)（务必与 AC 自动机上的 \(fail\) 区分）？就是点 \(u\) 维护的最短的串砍掉一个字符后的一个新的等价类。长度一定是连续的，因此我们说点 \(u\) 维护的子串的最短长度是 \(len_{link_u}+1\)，最长的是 \(len_u\)。

注意结论：对于一个字符串，你加长它会使等价类变小，缩短它会使等价类变长。

结论：一个点 \(u\) 的真实的 \(endpos\) 是它 \(fail\) 子树中的所有 \(endpos\) 的并。

现在开始增量构造。假如我们有一个 \(tail\) 表示上一次加入的那个整串。加入字符 \(r\)，新开一个 \(u\) 表示新的整串。时刻记住，我们要维护出边和后缀链接。

显然 \(ch_{tail,r}=u\)，从 \(tail\) 往上跳 \(link\) 到 \(p\)，这是在砍掉前缀，如果 \(ch_{t,r}=\varnothing\) 那么接上 \(ch_{p,r}=u\)。

如果 \(ch_{p,r}\neq\varnothing\)，因为我们在砍前缀，再砍它的出边也存在，所以我们在这里停下来更新。令 \(q=ch_{p,r}\)。我们很天真地想要 \(fail_u=q\)，这不好。

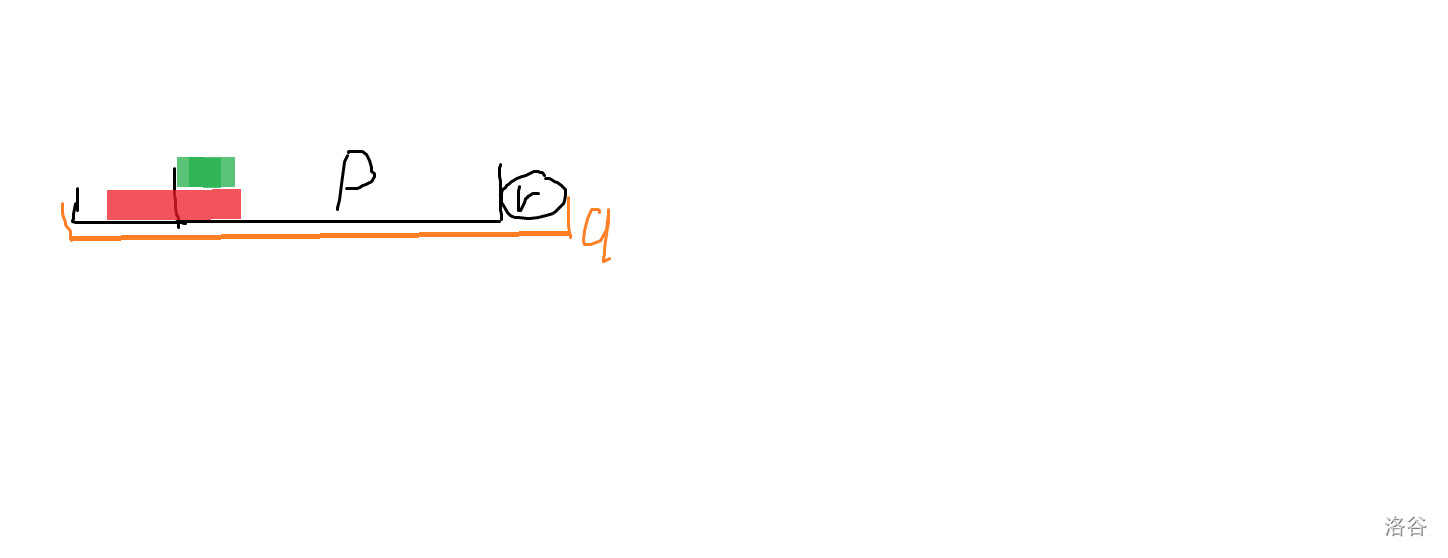
对于一个出现位置，有颜色的部分，是可能的子串左端点。显然 \(p\) 在这里面。如果 \(p\) 刚好是 \(q\) 的最短的字符串（绿色部分），那么直接 \(fail_u=q\) 是正确的。

否则（红色部分）我们就会发现，对于黑线右边的这一部分，它们的 \(endpos\) 的集合加上 \(n\)，但是左边这一部分不是，这两部分已经不一样了。

所以我们要分裂，假设我们分裂出 \(cq\)，那么使 \(cq\) 成为黑线右边这一部分，\(q\) 成为黑线左边的，根据定义，此时 \(fail_{cq}\) 为原来的 \(fail_q\)，\(fail_q\) 改成 \(fail_{cq}\)（因为等价类的大小，越往上跳越多）；\(fail_u=cq\)，就是说 \(u\) 贡献的这个 \(endpos\) 不会给到 \(q\)，这是正确的。对于 \(cq\) 的出边，和 \(q\) 是一模一样的。

对于 \(p\) 剩下的 \(fail\)，如果有 \(fail_{p',r}=q\) 那么改成 \(fail_{p',r}=cq\)。

现在维护 \(endpos\)，就是在我们建立的新的 \(u\) 那里打标记就行了。

现在升级成广义 SAM。

每次加入新的字符串，我们的 \(tail=root\)。这个时候注意：如果 \(ch_{tail,r}\) 已经存在，我们该分裂的分裂，反正不用在跳 \(fail\) 了。

很多细节，看代码。

时空复杂度 \(O(n)\)。

code

双倍空间捏！

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
template<int N,int M> struct suffixam{
	int ch[N<<1][M],link[N<<1],len[N<<1],tot;
	suffixam():tot(1){link[1]=0,len[1]=0;}
	int split(int r,int p,int q){
		if(len[q]==len[p]+1) return q;
		int u=++tot; len[u]=len[p]+1;
		memcpy(ch[u],ch[q],sizeof ch[0]);
		link[u]=link[q],link[q]=u;
		for(;p&&ch[p][r]==q;p=link[p]) ch[p][r]=u;
		return u;
	}
	int expand(int r,int p){
		if(ch[p][r]) return split(r,p,ch[p][r]);
		int u=++tot; len[u]=len[p]+1;
		for(;p;p=link[p]){
			if(ch[p][r]) return link[u]=split(r,p,ch[p][r]),u;
			else ch[p][r]=u;
		}
		return link[u]=1,u;
	}
};
int n,cnt[2000010];
LL ans;
char a[1000010];
suffixam<1000010,26> s;
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%s",a+1);
		int m=strlen(a+1),last=1;
		for(int j=1;j<=m;j++) cnt[last=s.expand(a[j]-'a',last)]++;
	}
	for(int i=2;i<=s.tot;i++) ans+=s.len[i]-s.len[s.link[i]];
	printf("%lld\n",ans);
	return 0;
}