日记 2023.10.5：2023 syzx 秋季训练 3

A

1. 不同元素个数只会减少不会增加。
2. 最终的 \(b\) 是若干段。
3. 若能在 \(a\) 中找到段的开头，则可以旋转得解（注意必须有一块的块长大于二，否则除了 \(a=b\) 外无法旋转）

故枚举 \(b_1\) 的匹配，分段后循环找 \(a\) 的对应，在循环一圈之前完成则有解。

若一开始 \(b_1=b_n\)，它们应该分成一段，需要做循环位移，使得 \(b_1\neq b_n\)。

\(O(n^2)\)。

B

相当于二进制的进位。因为只关心形态，从低往高做。

\(dp(pos, add)\) 枚举到 \(pos\)，进位是 \(add\)。\(dp(pos, add)\to dp(pos+1, add'),where\ add\in[0,(add+buc_{pos})/2]\)。

每个数字只会为后面 \(\log n\) 个地方产生贡献。是状态数少的离散 DP。前缀和优化一下。

C

打表找规律

D

a[i] = -a[i] === a[i] -= 2 * a[i]

即，操作后整个序列的总和不变。

考虑前缀和。

发现操作是交换前缀和。

• 相邻项交换直到有序：逆序对
• 任意两个元素交换直到有序：\(n-\) 置换环个数
• 任选一个元素删除并插入到其他位置：\(n-|LIS|\)

E

等价于选出两条边不交的链。分成两条链交在一点和不交两种情况，后者直接枚举一条边断开算子树内和子树外的直径。换根 DP 维护前四大的从这个点出发的链，随意玩玩。可以 \(O(n)\)？

F

相当于相邻两个中必须选一个，还有最前面和最后面。

meet in the middle。

枚举前一半和后一半，标记合法的。枚举后一半的时候，对不选的点相当于知道了前一半哪些必须选，所以对前一半的做高维前缀和，找一个必选点的超集中的最小价值。

\(O(2^{m/2}m)\)。

G

观察到如果可以将所有值绑在一起考虑那么操作次数是 \(O(n+q)\)。

考虑用并查集维护值的修改关系。对于操作一，新开点，然后记录当前点的值是它。操作三就拿出所有符合条件的值，暴力连父亲。\(O((n+q)\log n)\)。

H

路径肯定可以改成单调的。所以只考虑 \(a_l<a_r\)。

考虑从之前的某个关键点转移一部分答案。我们可以枚举一下是距离最近还是值最小，枚举一下发现是距离最近。就是对于 \(l\) 找到第一个 \(r\) 满足 \(a_r-a_l\leq k,a_r>a_l\)，然后 \(l\) 可以跳到 \(r\)，取 \(r\) 的答案；或者 \([a_l+1, a_r-1]\) 这一范围内的数字由 \(l\) 跳过去，还有 \(l\) 自己（因为 \(r\) 跳不了比他小的）。

使用一堆线段树。\(O(n\log n)\)。

I

限制相当于 \(\max(a_i, a_j)\geq \max(b_i, b_j)\land\min(a_i, a_j)\geq \min(b_i, b_j)\)。我们通过强制调整使得第二个限制被满足（直接将 \(\min(b_i, b_j)\) 分别对 \(a_i, a_j\) chkmax），这样只需要考虑第一个限制。这时候就有：\(a_i\geq b_i\) 或者 \(a_i\geq b_j\)，如果 \(a_i\geq b_i\land a_j\geq b_j\) 跳过，否则就是其中有一个 \(a_i\geq b_i\)，另外一个 \(a_i\leq a_j<b_j\)。我们将 \(a_i\geq b_i\) 划归 A 类点，\(a_i<b_i\) 划归 B 类点，则限制是在 A 类点和 B 类点之间的边，竟然是二分图。

于是对于 \(\max(a_i, a_j)\geq \max(b_i, b_j)\)，因为后面是常数，所以我们可以做最小割。

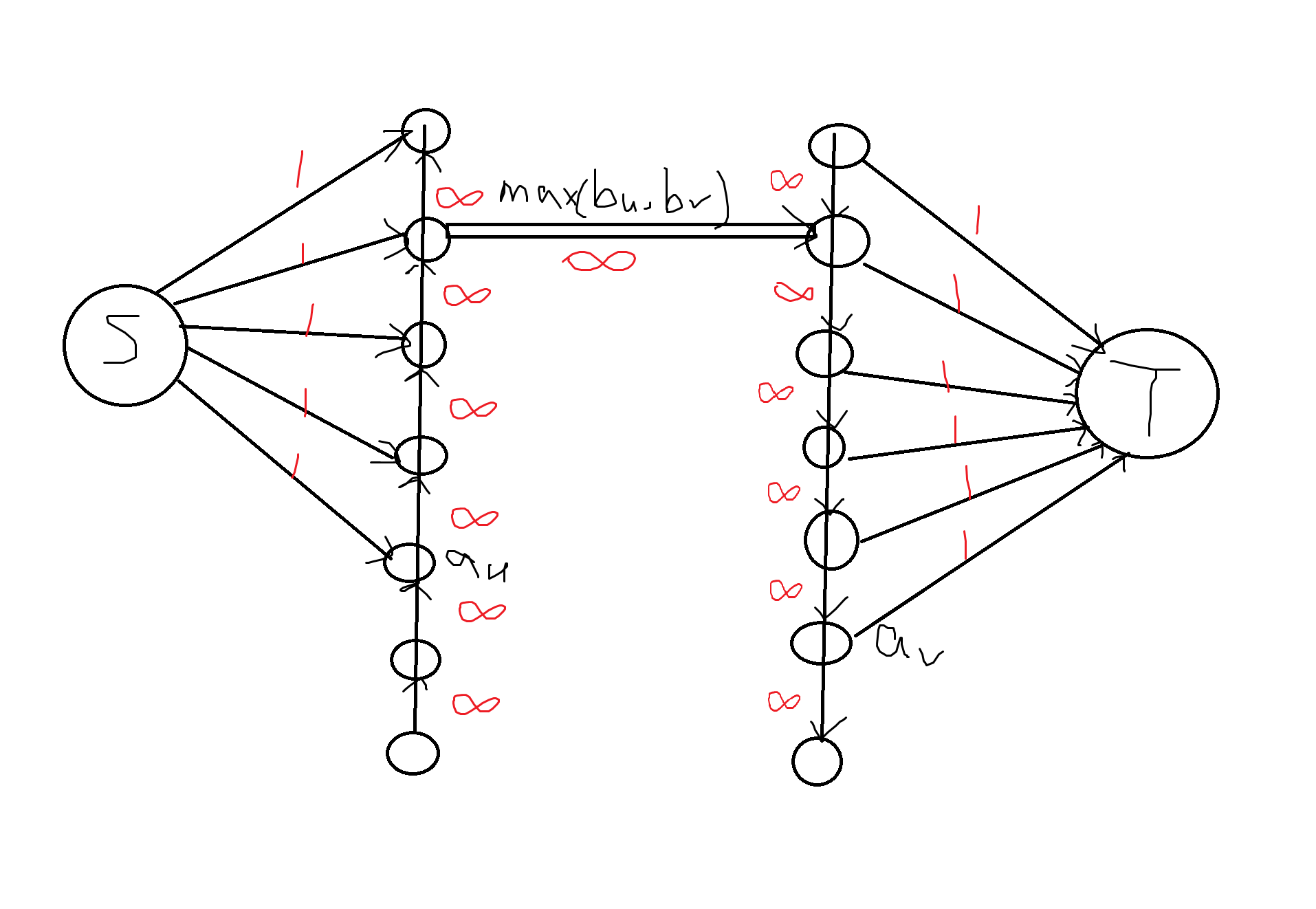
S 连 A 类点，T 连 B 类点，左边正链右边反链，就能完成题目限制。红色数字是边权。切完以后刚好是这样的。非常优美。