树状数组的学习
学习博客：https://www.cnblogs.com/wendster/p/treearray.html
树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和，但是每次只能修改一个元素的值；经过简单修改可以在log(n)的复杂度下进行范围修改，但是这时只能查询其中一个元素的值(如果加入多个辅助数组则可以实现区间修改与区间查询)。
树状数组和线段树很像，但能用树状数组解决的问题，基本上都能用线段树解决，而线段树能解决的树状数组不一定能解决。相比较而言，树状数组效率要高很多。
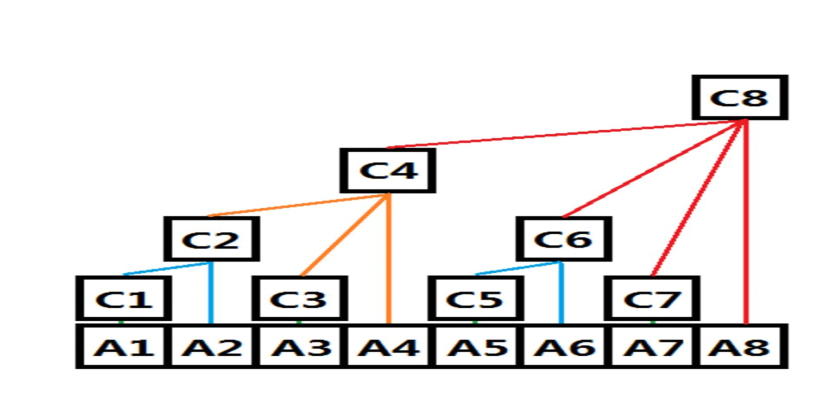
C1 = A1
C2 = A1 + A2
C3 = A3
C4 = A1 + A2 + A3 + A4
C5 = A5
C6 = A5 + A6
C7 = A7
C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
...
C16 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8 + A9 + A10 + A11 + A12 + A13 + A14 + A15 + A16
通过二进制，将数组的节点序号都转化成二进制。
就是这样的:
1--->001 C1 = A1
2--->010 C2 = A1 + A2
3--->011 C3 = A3
4--->100 C4 = A1 + A2 + A3 + A4
5--->101 C5 = A5
6--->110 C6 = A5 + A6
7--->111 C7 = A7
8--->1000 C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
但是这又有什么关系呢？
这里有一个有趣的性质：
设节点编号为x，那么这个节点管辖的区间为2^k（其中k为x二进制末尾0的个数）个元素。因为这个区间最后一个元素必然为Ax，
所以很明显：Cn = A(n – 2^k + 1) + A(n-2^k+2)+... + An
什么意思呢？举个栗子，1对应的二进制是001，二进制末尾0的个数为0，所以k=0，所以C1=A(1-2^k+1)+...An 就是C1=A(1-2^0+1)=A(1);
再来个栗子，4对应的二进制是100，二进制末尾0的个数为2，所以k=2，所以C4=A(4-2^2+1)+A(4-2^2+2)+...+A(4)=A(1)+A(2)+A(3)+A(4);
再搞不懂就自己再手推几个数试试就可以了。
至于怎么得出来的这个神奇的东西，就是靠二进制。
接下来就是怎么代码实现这个呢？
就是要靠神奇的lowbit了。
int lowbit(int x)
{
return x&(-x);
}
x&(-x)就是整数x与其相反数(负号取反)的按位与:相同位的两个数字都为1，则为1；若有一个不为1，则为0，即:1&1=1,0&1=0,0&0=0;
计算机中负数使用对应正数的补码来表示。
-x就是x对应的二进制数先各位取反，0变成1，1变成0。然后最低位加1。
举个栗子，4对应二进制为100；-4对应的为011+1=100，所以为(100)&(100)所以为100。
知道这个就可以进行区间查询啦。
区间查询利用C[i]求A数组前i个的和；
//代码1：
int SUM(int n)
{
int s=0;
while(n>0){
s+=c[n];
n-=lowbit(n);
}
return s;
}
//代码2：
int SUM(int n)
{
int s=0;
for(int i=n;i>0;i-=lowbit(i))
s+=c[i];
return s;
}
两个代码哪个好理解就理解哪个。
接着刚刚举的栗子4，求A数组前4个数的和；
lowbit(4)得出100；然后100就是4，所以为s+=c[4];此时i=4,4-lowbit(4)=100-100=0;结束。
再举个栗子7，求前7个数的和，就是s+=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7];
因为
1--->001 C1 = A1
2--->010 C2 = A1 + A2
3--->011 C3 = A3
4--->100 C4 = A1 + A2 + A3 + A4
5--->101 C5 = A5
6--->110 C6 = A5 + A6
7--->111 C7 = A7
8--->1000 C8 = A1 + A2 + A3 + A4 + A5 + A6 + A7 + A8
所以为C[4]+C[6]+C[7];
就是C[100]+C[110]+C[111];
首先s+=c[7];
然后lowbit[7]=(111)&(001)=001;此时i=7,所以为7-lowbit(7)=111-001=110,110就是6;s+=c[6];
lowbit(6)=(110)&(010)=010;此时i=6,所以为6-lowbit(6)=110-010=100,100就是4;s+=c[4];
lowbit(4)=(100)&(100)=100;此时i=4,所以为4-lowbit(4)=100-100=0,结束。
所以得到A数组中前7个数的和为C[7]+C[6]+C[4];
不懂的话再自己手推一个数就差不多懂了。
接下来就是单点更新。
单点更新要从下往上依次更新。
//代码1:
void add(int x)
{
while(x<=N){
++a[x];
x+=lowbit(x);
}
}
//代码2:
void add(int x,int y)
{
for(int i=x;i<=n;i+=lowbit(i))
c[i]+=y;
}
更新过程仔细想一想就是查询过程的逆过程；
举个栗子，更新A1,还要继续更新C[1],C[2],C[4],C[8];
就是C[001],C[010],C[100],C[1000];
i=1;C[1]+=A[1];
lowbit(1)=(001)&(001)=001;此时i=1,所以为1+lowbit(1)=001+001=010,010就是2;C[2]+=A[1];
lowbit(2)=(010)&(110)=010;此时i=2,所以为2+lowbit(2)=010+010=100,100就是4;C[4]+=A[1];
lowbit(4)=(100)&(100)=100;此时i=4,所以为4+lowbit(4)=100+100=1000,1000就是8;C[8]+=A[1];结束。
