矩阵快速幂的学习(系统的学习)

学习博客：https://www.cnblogs.com/cmmdc/p/6936196.html

                  https://www.cnblogs.com/yan-boy/archive/2012/11/29/2795294.html

首先看看整数快速幂的用处：

如果我们要求x^19,一般思想是for循环来做，这样的话要循环19次，如果次方数太大的话，显然是很要时间的，如果用矩阵快速幂的方法的话，可以接着看：

19的二进制表示=10011;  x^19=x^16*x^2*x^1，看看16，2，1是怎么来的，其实就是19的二进制上面的1对应的值，所以依靠这个我们可以超级快的求出来x^19次方

下面看代码的解释：

#include<iostream>
#include<string.h>
#include<map>
#include<cstdio>
#include<cstring>
#include<stdio.h>
#include<cmath>
#include<ctype.h>
#include<math.h>
#include<algorithm>
#include<set>
#include<queue>
typedef long long ll;
using namespace std;
const ll mod=1e9+7;
const int maxn=1e4+10;
const int maxk=5e3+10;
const int maxx=1e4+10;
const ll maxe=1000+10;
#define INF 0x3f3f3f3f3f3f
#define Lson l,mid,rt<<1
#define Rson mid+1,r,rt<<1|1
int Quickpow(int x,int n)
{
    int ans=1,res=x;
    while(n)//这里看不太懂的话自己模拟一下
    {
        if(n&1)
        {
            ans*=res;
        }
        res*=res;
        n>>=1;
    }
    return ans;
}
int main()
{
    int n,x;
    cin>>x>>n;//求x^n次方
    cout<<Quickpow(x,n)<<endl;
    return 0;
}

下面看看矩阵快速幂：

 讲解一道题目来理解：

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1575

Tr A

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 7332    Accepted Submission(s): 5384


Problem Description
A为一个方阵，则Tr A表示A的迹（就是主对角线上各项的和），现要求Tr(A^k)%9973。
 

 

Input
数据的第一行是一个T，表示有T组数据。
每组数据的第一行有n(2 <= n <= 10)和k(2 <= k < 10^9)两个数据。接下来有n行，每行有n个数据，每个数据的范围是[0,9]，表示方阵A的内容。
 

 

Output
对应每组数据，输出Tr(A^k)%9973。
 

 

Sample Input
2 2 2 1 0 0 1 3 99999999 1 2 3 4 5 6 7 8 9
 

 

Sample Output
2 2686
 

 

Author
xhd
 

 

Source
HDU 2007-1 Programming Contest
 

 

Recommend
linle   |   We have carefully selected several similar problems for you:  1757 1588 2256 2604 2254 
 
思路： 没什么思路，其实就是一道矩阵快速幂的裸题，具体看代码：
#include<iostream>
#include<string.h>
#include<map>
#include<cstdio>
#include<cstring>
#include<stdio.h>
#include<cmath>
#include<ctype.h>
#include<math.h>
#include<algorithm>
#include<set>
#include<queue>
typedef long long ll;
using namespace std;
const ll mod=9973;
const int maxn=1e4+10;
const int maxk=5e3+10;
const int maxx=1e4+10;
const ll maxe=1000+10;
#define INF 0x3f3f3f3f3f3f
#define Lson l,mid,rt<<1
#define Rson mid+1,r,rt<<1|1
int n;
ll k;
struct matrix
{
    int a[15][15];
}ans,res;
void init()
{
    memset(ans.a,0,sizeof(ans.a));
    for(int i=0;i<n;i++)
    {
        ans.a[i][i]=1;//相当于整数快速幂里面的初值1 ，这里是一个单位矩阵
        for(int j=0;j<n;j++)
        {
            cin>>res.a[i][j];//初值
        }
    }
}
matrix multiply(matrix x,matrix y)
{
    matrix temp;
    memset(temp.a,0,sizeof(temp.a));
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            for(int l=0;l<n;l++)
            {
                temp.a[i][j]+=x.a[i][l]*y.a[l][j];
                if(temp.a[i][j]>mod) temp.a[i][j]%=mod;
            }
        }
    }
    return temp;
}
void Quickpow()
{
    while(k)
    {
        if(k&1)
        {
            ans=multiply(ans,res);//这里跟整数快速幂几乎一样
        }
        res=multiply(res,res);
        k>>=1;
    }
}
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        ll sum=0;
        cin>>n>>k;
        init();
        Quickpow();
        for(int i=0;i<n;i++)
            sum+=ans.a[i][i];
            sum%=mod;
        cout<<sum<<endl;
    }
    return 0;
}

 下面看一道应用题：

题目链接：http://poj.org/problem?id=3070

Fibonacci
Time Limit: 1000MS   Memory Limit: 65536K
Total Submissions: 19383   Accepted: 13413

Description

In the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

An alternative formula for the Fibonacci sequence is

.

Given an integer n, your goal is to compute the last 4 digits of Fn.

Input

The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.

Output

For each test case, print the last four digits of Fn. If the last four digits of Fn are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print Fn mod 10000).

Sample Input

0
9
999999999
1000000000
-1

Sample Output

0
34
626
6875

Hint

As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by

.

Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:

.

Source

Stanford Local 2006
 
题目大意：就是求斐波那契数列
 
思路：首先我们要构造一个矩阵快速幂，一般把一道题转化为矩阵快速幂分为两步：
第一步：写出递推式，在这里是a[n]=a[n-1]+a[n-2]
第二步：把递推式转化为矩阵快速幂，那么我们要构造一个矩阵的n次方
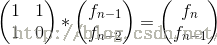,简写成T * a[n-1]=a[n]，T矩阵就是那个2*2的常数矩阵，而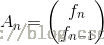

这里就是个矩阵乘法等式左边:1*f(n-1)+1*f(n-2)=f(n);1*f(n-1)+0*f(n-2)=f(n-1);

这里还是说一下构建矩阵递推的大致套路,一般a[n]与a[n-1]都是按照原始递推式来构建的，当然可以先猜一个a[n],主要是利用矩阵乘法凑出矩阵T,第一行一般就是递推式，后面的行就是不需要的项就让与其的相乘系数为0。矩阵T就叫做转移矩阵(一定要是常数矩阵),它能把a[n-1]转移到Aa[n];然后这就是个等比数列，直接写出通项:此处A1叫初始矩阵。所以用一下矩阵快速幂然后乘上初始矩阵就能得到a[n],这里a[n]就两个元素(两个位置)，根据自己设置的a[n]对应位置就是对应的值，按照上面矩阵快速幂写法，ans.a[0][0]=f(n)就是我们要求的。

注意构造的时候要构造为一个方阵，就是在原来构造的基础上补上0

看代码：

#include<iostream>
#include<string.h>
#include<map>
#include<cstdio>
#include<cstring>
#include<stdio.h>
#include<cmath>
#include<ctype.h>
#include<math.h>
#include<algorithm>
#include<set>
#include<queue>
typedef long long ll;
using namespace std;
const ll mod=10000;
const int maxn=1e9+10;
const int maxk=5e3+10;
const int maxx=1e4+10;
const ll maxe=1000+10;
#define INF 0x3f3f3f3f3f3f
#define Lson l,mid,rt<<1
#define Rson mid+1,r,rt<<1|1
int n;
struct matrix
{
    ll a[3][3];
}ans,res;
void init()
{
    res.a[0][0]=1;
    res.a[0][1]=1;
    res.a[1][0]=1;
    res.a[1][1]=0;
    ans.a[0][0]=1;
    ans.a[0][1]=0;
    ans.a[1][0]=0;
    ans.a[1][1]=1;
}
matrix multiply(matrix x,matrix y)
{
    matrix temp;
    memset(temp.a,0,sizeof(temp.a));
    for(int i=0;i<2;i++)
    {
        for(int j=0;j<2;j++)
        {
            for(int k=0;k<2;k++)
            {
                temp.a[i][j]=(temp.a[i][j]+x.a[i][k]*y.a[k][j])%mod;
            }
        }
    }
    return temp;
}
void Quickpow()
{
    while(n)
    {
        if(n&1)
        {
            ans=multiply(ans,res);
        }
        res=multiply(res,res);
        n>>=1;
    }
}
int main()
{
    while(cin>>n)
    {
        if(n==-1) break;
        if(n==0) cout<<0<<endl;
        else if(n==1) cout<<1<<endl;
        else
        {
            n--;
            init();
            Quickpow();
            cout<<ans.a[0][0]<<endl;
        }
    }
    return 0;
}

 

给一些简单的递推式
1.f(n)=a*f(n-1)+b*f(n-2)+c；（a,b,c是常数）

2.f(n)=c^n-f(n-1) ；（c是常数）

 

posted @ 2018-09-14 17:06  执||念  阅读(350)  评论(0)  编辑  收藏  举报