2006 飞行员配对(二分图最大匹配)

学习博客：https://www.cnblogs.com/fu3638/p/8784826.html

二分图匹配

基本概念：

给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两条边都不依附于同一个顶点，则称M是一个匹配。

通常分为以下几种匹配：

一、 最大匹配

指在当前已完成的匹配下,无法再通过增加未完成匹配的边的方式来增加匹配的边数。这个问题通常使用匈牙利算法解决，朴素时间复杂度为O（V^3）,使用邻接表的前提下时间复杂度为O（VE）。还有一种对匈牙利进行了优化的Hopcroft-Karp算法，时间复杂度为O（sqrt（V）*E）。

二、 完全匹配（完备匹配）

是在最大匹配下的一种特殊情况，指在二分图的两个集合中的点两两都能够得到匹配。

三、 最佳匹配

节点带有权值，在能够完全匹配的前提下，选择匹配方案使得权值之和最大。这个问题通常使用KM算法解决，时间复杂度O(V^3)。

 

算法介绍：

一、    匈牙利算法

1、基本概念：

1）交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边...形成的路径叫交替路。

2）增广路：从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），则这条交替路称为增广路（agumenting path）。

如下图所示：

 

 

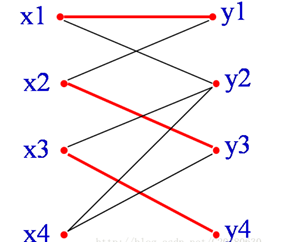
红边为三条已经匹配的边。从X部一个未匹配的顶点x4开始，能找到一条增广路：
x4->y3->x2->y1->x1->y2   所以到最后就是x1->y2   x2->y1  x3-y4  x4->y3

由增广路的定义可以推出下述三个结论：

①增广路的路径长度必定为奇数，第一条边和最后一条边都不属于M（已匹配子图），因为两个端点分属两个集合，且未匹配。

②增广路经过取反操作（已匹配边变为未匹配边，未匹配边变为已匹配边）可以得到一个更大的匹配M’。

③M为G的最大匹配当且仅当不存在相对于M的增广路径。

2、匈牙利算法能解决的问题：

1)最大匹配

最大匹配的匹配边的数目。

2)最小点覆盖数

二分图的最小点覆盖数=最大匹配数（König定理）

这里说明一下什么是最小点覆盖：假如选了一个点就相当于覆盖了以它为端点的所有边，你需要选择最少的点来覆盖所有的边。

3）最小路径覆盖

最小路径覆盖＝顶点数－最大匹配数

在一个N*N的有向图中，路径覆盖就是在图中找一些路经，使之覆盖了图中的所有顶点，

且任何一个顶点有且只有一条路径与之关联；（如果把这些路径中的每条路径从它的起始点走到它的终点。

最小路径覆盖就是找出最小的路径条数，使之成为G的一个路径覆盖。

由上面可以得出：

 ①一个单独的顶点是一条路径；

 ②如果存在一路径p1,p2,......pk，其中p1 为起点，pk为终点，那么在覆盖图中，顶点p1,p2,......pk不再与其它的顶点之间存在有向边。

4）最大独立集

最大独立集=顶点数-最大匹配数。

独立集：图中任意两个顶点都不相连的顶点集合。

3、算法实现(别的博客找的)

我们以下图为例说明匈牙利匹配算法。

 

 

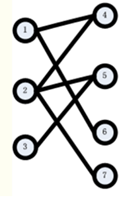
step1：从1开始，找到右侧的点4，发现点4没有被匹配，所以找到了1的匹配点为4 。得到如下图：

 

 

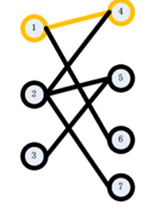
step2：接下来，从2开始，试图在右边找到一个它的匹配点。我们枚举5，发现5还没有被匹配，于是找到了2的匹配点，为5.得到如下图：

 

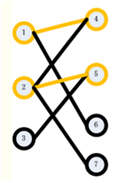
step3:接下来，我们找3的匹配点。我们枚举了5，发现5已经有了匹配点2。此时，我们试图找到2除了5以外的另一个匹配点，我们发现，我们可以找到7，于是2可以匹配7，所以5可以匹配给3，得到如下图：

 

 

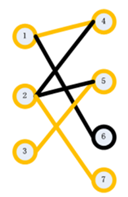
此时，结束，我们得到最大匹配为3。

匈牙利算法的本质就是在不断寻找增广路，直到找不到位置则当前的匹配图就是最大匹配。

题目链接：https://www.51nod.com/Challenge/Problem.html#!#problemId=2006

看代码：

#include<iostream>
#include<algorithm>
#include<stack>
#include<cstdio>
#include<map>
#include<queue>
#include<cstring>
using namespace std;
typedef long long LL;
const int maxn=1e2+5;
vector<int>v[maxn];
int link[maxn];//link[y]=x 即y和x匹配
bool vis[maxn];
int N,M;

//用dfs寻找增广路
bool dfs(int u)
{
    for(int i=0;i<v[u].size();i++)//遍历所有与u能够匹配的飞行员
    {
        int t=v[u][i];
        if(!vis[t])//本次查找还没有走过这个点 走过就不需要在走了
        {
            vis[t]=true;
            if(link[t]==-1||dfs(link[t]))//如果t尚未被匹配  或者link[t] 能够找到其它能够替代的点 则把t点让给u
            {
                link[t]=u;
                return true;
            }
        }
    }
    return false;//找不到能与自己匹配的飞行员
}

//返回最大匹配数
int max_match()
{
    memset(link,-1,sizeof(link));
    int ans=0;
    for(int i=1;i<=N;i++)//遍历二分图左边的所有点
    {
        memset(vis,false,sizeof(vis));//每次查找一个新的点都需要标记所有点没有走过 因为是一次新的查找
        if(dfs(i)) ans++;
    }
    return ans;
}
int main()
{

    cin>>N>>M;
    int a,b;
    while(cin>>a>>b)
    {
        if(a==-1&&b==-1) break;
        v[a].push_back(b);//a和b可以匹配
    }
    int t=max_match();
    if(t==0) cout<<"No Solution!"<<endl;
    else cout<<t<<endl;
    return 0;
}