出栈次序

题目： 

X星球特别讲究秩序，所有道路都是单行线。
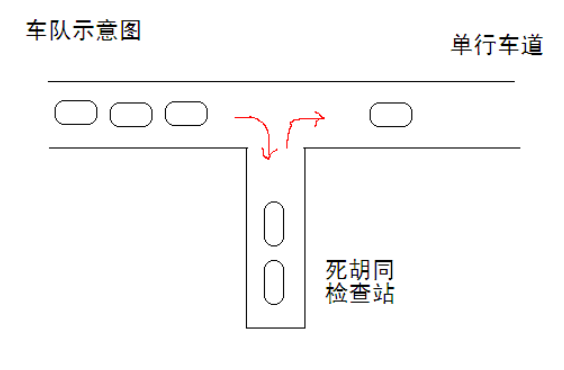
一个甲壳虫车队，共16辆车，按照编号先后发车，夹在其它车流中，缓缓前行。

路边有个死胡同，只能容一辆车通过，是临时的检查站，如图所示。
X星球太死板，要求每辆路过的车必须进入检查站，也可能不检查就放行，也可能仔细检查。
如果车辆进入检查站和离开的次序可以任意交错。那么，该车队再次上路后，可能的次序有多少种？

为了方便起见，假设检查站可容纳任意数量的汽车。
显然，如果车队只有1辆车，可能次序1种；2辆车可能次序2种；3辆车可能次序5种。

 

思路：这题说实话 ，唯一想到的是暴力，枚举每一种可能的情况，再判断是否可以行得通，但是很快就否决了，因为16个数的全排列根本数不清，16^16  太大了，然后没什么思路，看了

题解，是这么说的，其实就是找规律，下面具体看一下怎么做出来的：

我们把n个元素的出栈个数的记为f(n), 那么对于1,2,3, 我们很容易得出：

 

                                  f(1) = 1     //即 1

                                     f(2) = 2     //即 12、21

                                     f(3) = 5     //即 123、132、213、321、231

 

然后我们来考虑f(4), 我们给4个元素编号为a,b,c,d, 那么考虑：元素a只可能出现在1号位置，2号位置，3号位置和4号位置(很容易理解，一共就4个位置，比如abcd,元素a就在1号位置)。

分析：

 

1) 如果元素a在1号位置，那么只可能a进栈，马上出栈，此时还剩元素b、c、d等待操作，就是子问题f(3)；

2) 如果元素a在2号位置，那么一定有一个元素比a先出栈，即有f(1)种可能顺序（只能是b），还剩c、d，即f(2)，     根据乘法原理，一共的顺序个数为f(1) * f(2)；

3) 如果元素a在3号位置，那么一定有两个元素比1先出栈，即有f(2)种可能顺序（只能是b、c），还剩d，即f(1)，

    根据乘法原理，一共的顺序个数为f(2) * f(1)；

4) 如果元素a在4号位置，那么一定是a先进栈，最后出栈，那么元素b、c、d的出栈顺序即是此小问题的解，即f(3)；

 

结合所有情况，即f(4) = f(3) + f(2) * f(1) + f(1) * f(2) + f(3);

为了规整化，我们定义f(0) = 1；于是f(4)可以重新写为：

f(4) = f(0)*f(3) + f(1)*f(2) + f(2) * f(1) + f(3)*f(0) 

 

然后我们推广到n，推广思路和n=4时完全一样，于是我们可以得到：

f(n) = f(0)*f(n-1) + f(1)*f(n-2) + ... + f(n-1)*f(0)

看代码：

#include<iostream>
#include<stack>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn=100;
ll a[maxn];
//f(n) = f(0)*f(n-1) + f(1)*f(n-2) + ... + f(n-1)*f(0)
void solve(int x)
{
    ll sum=0;
    for(int i=0;i<x;i++) sum+=a[i]*a[x-1-i];
    a[x]=sum;
}
int main()
{
    a[0]=1;
    a[1]=1;
    a[2]=2;
    a[3]=5;
    for(int i=4;i<=16;i++) solve(i);

    cout<<a[16]<<endl;
    return 0;
}