树形dp学习

学习博客：https://www.cnblogs.com/qq936584671/p/10274268.html

树的性质：n个点，n-1条边，任意两个点之间只存在一条路径，可以人为设置根节点，对于任意一个节点只存在至多一个父节点，其余为子节点。

记忆化树形dp模型较为抽象难以理解，以下通过由浅到深的方式解析树形dp以及树的性质。

树形dp求树的直径：（在一颗树里找到点X，Y，使得|XY|最大）

 

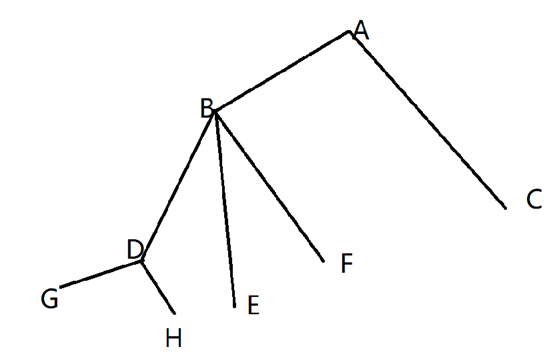
如图，我们令A为根节点，令dfs遍历顺序为ABDGHEFC。

在我们的dfs计算过程中，我们从下往上求解每一个节点，总的来说我们要求两个东西：

1、以每一个节点为根，所能到达的最长路径dp【u】

2、以每一个节点为根，它下面的的树的最长路径ans（其实就是找到 两个没有重复路径的子树，例如以B为根节点，会找到BDG+BE而不会找到BDG+BDH）

然后将子树中以子树根为起点所能到达的最长路径传给父节点，最后得出答案

具体看下面代码：

struct Node
{
    int nex,val;
};
vector<Node>node[maxn];//node[u][i].nex代表该节点的子节点  node[u][i].val代表该节点与子节点之间路径的权值
void dfs(int u,int fa)//该节点和该节点的父亲
{
    for(int i=0;i<node[u].size();i++)
    {
        int v=node[u][i].nex;
        if(v!=fa)//防止回到父节点
        {
            dfs(v,u);//
            ans=max(ans,d[u]+d[v]+node[u][i].val);//这个必须在下面一步的前面
            d[u]=max(d[u],d[v]+node[u][i].val);
        }
    }
}

 

理解了基本的树形dp之后，开始下面的练习：

 题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=4616

学习链接：https://www.cnblogs.com/zyb993963526/p/7223861.html

题目大意：在一颗有n（n<5e4）个节点的树中，每个节点有权值和是否有陷阱，你可以最多踏进c（c<=3）个陷阱，当你进入第c个陷阱时，你就无法继续移动了，你可以在任意节点出发，获取经过节点的权值（无法重复获取同一个节点），求能得到的最大权值和。

思路：

有点像树链剖分，对于一个以u为根的子树，因为每个顶点只能经过一次，那我们只能选择它的一个子树往下走。就像是把这棵树分成许多链，最后再连接起来。

这道题目麻烦的地方是陷阱的处理，用d【u】【j】【0/1】表示以u为根的某一子节点经过j个陷阱后到达u的最大权值和，0/1表示起点是否有陷阱。

 

假设当前到达u时经过了k个陷阱，分下面几种情况进行讨论：

①如果k==c，那么起点和终点至少有一个是陷阱（可能有些人会认为终点一定会是陷阱，这样是没错的，因为起点和终点时相对的，你也可以把起点看做终点）。

②如果k<c，那么起点和终点是否是陷阱是任意的，可以有也可以没有。

具体看代码：

#include<iostream>
#include<vector>
#include<math.h>
#include<string.h>
using namespace std;
const int maxn=50000+5;
int n,c;
int ans;
vector<int>G[maxn];
int val[maxn],trap[maxn];//分别存储节点的值和是否有陷阱
int d[maxn][5][2];//d[u][j][0/1]表示以u为根的某一子节点经过j个陷阱之后到达u的最大权值和
void dfs(int u,int fa)
{
    d[u][trap[u]][trap[u]]=val[u];

    //计算以u为根的子树所能获得的最大值，也就是将子树的链进行连接
    for(int i=0;i<G[u].size();i++)
    {
        int v=G[u][i];
        if(v!=fa)
        {
            dfs(v,u);
            for(int j=0;j<=c;j++)
            {
                for(int k=0;j+k<=c;k++)
                {
                    if(j!=c) ans=max(ans,d[u][j][0]+d[v][k][1]);
                    if(k!=c) ans=max(ans,d[u][j][1]+d[v][k][0]);
                    if(j+k<c) ans=max(ans,d[u][j][0]+d[v][k][0]);//起点和终点都可以为非陷阱
                    if(j+k<=c) ans=max(ans,d[u][j][1]+d[v][k][1]);//起点和终点都可以为陷阱

                }
            }
            for(int j=0;j+trap[u]<=c;j++)
            {
                d[u][j+trap[u]][0]=max(d[u][j+trap[u]][0],d[v][j][0]+val[u]);
                if(j!=0)
                {
                    d[u][j+trap[u]][1]=max(d[u][j+trap[u]][1],d[v][j][1]+val[u]);
                }
            }
        }
    }
}
int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        cin>>n>>c;//n个节点 最多可以踩c个陷阱
        for(int i=0;i<n;i++) G[i].clear();
        for(int i=0;i<n;i++) cin>>val[i]>>trap[i];//输入值和是否有陷阱
        for(int i=1;i<n;i++)
        {
            int u,v;
            cin>>u>>v;
            G[u].push_back(v);
            G[v].push_back(u);
        }
        ans=0;
        memset(d,0,sizeof(d));
        dfs(0,-1);
        cout<<ans<<endl;
    }
}