CF911F [Tree Destruction] 题解
链接
WC讲的第二道例题,被一分钟带过,我裂开了
首先知道一个比较显然的东西,对于一个点,距离最长的点必定是该树的直径的其中一个端点。
虽然这个挺显然的,不过还是证一下(老师昨天一秒带过太让人炸裂了)(这里用一个反证法吧)
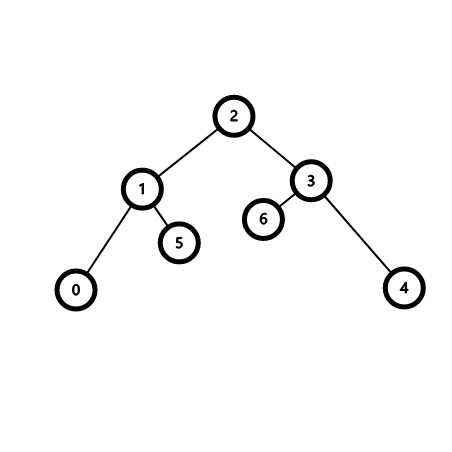
设 \(0,4\) 为直径两端,\(5,6\) 为直径外两点
若 \(5->6\) 为最长的链,那么 \(1->6\) 会大于 \(1->4\)
那么直径就会变成 \(0->6\) 这与前提矛盾,所以对于 \(5\) ,\(4\) 是最优的选择,对 \(6\),\(0\) 是最优的选择
然后怎么整呢,我们先把直径搞出来,对于每一个点,选择一个端点使得链最长,最后再按顺序删掉链上的所有点
然后想一下细节(会的同志可以直接开始写了)
对于一个点,可能有两种情况(这里使用换根法,没考虑不使用的做法)
- 1.与上面的端点匹配
- 2.与下面的端点匹配
怎么找到最优的端点,还要计算长度呢,我们想到了经典的 \(dep_x+dep_y-2*dep_{lca_{x,y}}\)
又想到,因为其中一个端点是在链上的,所以两点的 \(lca\)也会在链上
于是我们在 \(dfs\) 的时候,记录一个 \(top\) ,表示在 \(dfs\) 过程中上一个找到的一个在链上的点,这个点一定就是 \(lca\)了
这是考虑下面哪个端点,而与上面端点匹配的情况其实我们求过了
由于是换根法,根节点就是上面的端点,所以直接用 \(dep\) 值就好
啊,本人语文不好,如果看不懂也别慌,结合代码还是比较好懂得
#include<iostream>
#include<cstdio>
#include<cstring>
#define ll long long
using namespace std;
const ll N=2e5+10;
ll n,m,cnt,head[N],dep[N],faa[N],toper;
ll ans,Ans,final_ans,Time;
bool on[N];
struct answer{
ll a,b,c;
}A[N];
struct star_platinum{
ll to,nxt;
}q[N*3];
inline void add(ll u,ll v){
q[++cnt].to=v,q[cnt].nxt=head[u],head[u]=cnt;
q[++cnt].to=u,q[cnt].nxt=head[v],head[v]=cnt;
}
void dfs1(ll x,ll fa){
if(Time==0&&dep[x]>dep[ans])ans=x;
if(Time==1&&dep[x]>dep[Ans])Ans=x;
for(ll i=head[x];i;i=q[i].nxt){
ll v=q[i].to;
if(v!=fa){
dep[v]=dep[x]+1;
dfs1(v,x);
}
}
}
void dfs2(ll x,ll fa){
for(ll i=head[x];i;i=q[i].nxt){
ll v=q[i].to;
if(v!=fa){
dfs2(v,x);
faa[v]=x;
if(on[v])on[x]=1;
}
}
}
void dfs3(ll x,ll fa,ll topf){
for(ll i=head[x];i;i=q[i].nxt){
ll v=q[i].to;
if(fa!=v){
if(on[v])dfs3(v,x,v);
else dfs3(v,x,topf);
}
}
if(!on[x]){
if(dep[x]>dep[x]+dep[Ans]-(dep[topf]*2)){
final_ans+=dep[x];
A[++toper]=(answer){x,ans,x};
}
else {
final_ans+=dep[x]+dep[Ans]-(dep[topf]*2);
A[++toper]=(answer){Ans,x,x};
}
}
}
int main(){
scanf("%lld",&n);
for(ll a1,a2,i=1;i<n;i++){
scanf("%lld%lld",&a1,&a2);
add(a1,a2);
}
dfs1(1,0);
memset(dep,0,sizeof(dep)),Time++;
dfs1(ans,0);
on[Ans]=1;
dfs2(ans,0);
dfs3(ans,0,ans);
for(ll i=Ans;i!=ans;i=faa[i]){
final_ans+=dep[i];
A[++toper]=(answer){ans,i,i};
}
printf("%lld\n",final_ans);
for(ll i=1;i<=toper;i++){
printf("%lld %lld %lld\n",A[i].a,A[i].b,A[i].c);
}
}


