状压dp技巧之轮廓线 hdu1400/poj2411\acwing291 蒙德里安的梦想

我蒙德里安有一个梦想,就是成为方块填充之王!
POJ地址//HDU地址//acwing地址
(!注意,学习此方法需要一定状压基础,请至少做两道状压\(DP\)再学习)
一开始我脑中蹦出了状压整张图的想法,但显然不行,这时想一下,其实我们在乎的方格并不多,其实只需要一行
但是方块又有两种摆放方法,不能只存上一行,还需要知道左边的方格的信息,于是有大佬就发明了这个轮廓线做法
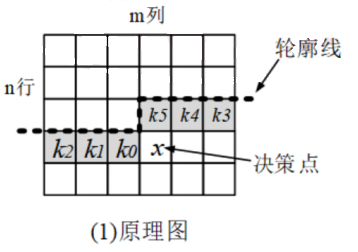
如图,\(x\)为\(dp\)过程中枚举的转移点,虚线即为轮廓线,我们状压轮廓线下的所有方块是否被覆盖
我们可以在\(k5=0\)时放置竖着的方块,在\(k5!=0\)时不放方块或在\(k0=0\)和\(k5!=0\)同时成立时在\(x\)处放置横向的方块(整张图必须填满)
如此甚好,然后我们便可以将轮廓往右推,如图

这样便能在下次继续转移,那么如何实现右移?
首先将整个状态\(k\)右移(即k<<=1),然后将第一位赋为\(1\)(当\(x\)上放置了方块时)
对于放置竖着的方块,我们将\(k5\)赋为\(0\)(因为已经溢出了,不予考虑)
对于横着的方块我们将\(k0\)(第二位)赋为\(1\)
若我们没有放置方块,那么此时\(k5\)时有值的,需要和情况一样赋为\(0\)
#include<iostream>
#include<cstdio>
#include<cstring>
#define ll long long
using namespace std;
ll f[3][100000],n,m,mst,now,old;
int main(){
scanf("%lld%lld",&n,&m);
while(n&&m){
mst=(1<<m)-1;
now=0,old=1;
memset(f,0,sizeof(f));
f[now][mst]=1;
for(ll i=1;i<=n;++i){
for(ll j=1;j<=m;++j){
swap(old,now);
memset(f[now],0,sizeof(f[now]));
for(ll k=0;k<=mst;++k){
if(k&(1<<(m-1))){
f[now][(k<<1)&(~(1<<m))]+=f[old][k];
if(j>1&&!(k&1))f[now][((k<<1)|3)&(~(1<<m))]+=f[old][k];
}
if(i>1&&!(k&(1<<(m-1))))f[now][(k<<1)^1]+=f[old][k];
}
}
}
printf("%lld\n",f[now][mst]);
scanf("%lld%lld",&n,&m);
}
}


