CF1292F Nora's Toy Boxes详细の题解
题面
啊,虽然昨晚被所有人爆踩了,但是在烦了广东队长一晚上后(俟其欣悦,俯身倾耳以请)
卒获有所闻(虽然还是有不少东西不懂,望指出)
首先把题目条件转变一下,把\(a_{i}|a_{j}\)视为\(i\)向\(j\)连边,然后我们就构建出了一个\(DAG\)
于是题目就变成了每次在\(DAG\)上删一个合法的点,问将每个弱连通块删的只剩2个点的方案数(毕竟题目要求了三个点中删一个点,所以最后剩两个)
那么答案就是每个连通块内答案的乘积
然而并没有办法直接计算删点方案数,所以考虑如何加点
我们留意到,在每个连通块内其实只有两种点:有可能被删的点,和绝对不会被删的点(可以看做根节点)
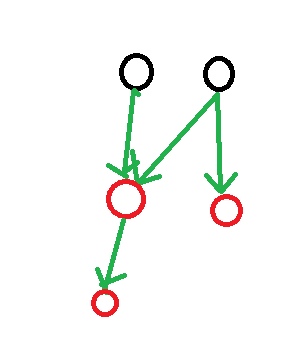
如图,黑色点删不了
而红色点无论在第几层都没啥区别(针对许多dp成瘾的小伙伴,这里不需要分层dp)
设所有黑色点为集合\(S\),所有红色点集合为\(T\)
口胡一个状态:\(dp_{s,t}\),\(t\)是我们已添加的点的集合,\(s\)则是所有与\(t\)中的点有连接的,且在\(S\)中的点的集合,所以
但是状态太多,直接爆炸,所以考虑把\(t\)改成其他东西,就改成已添加的点数好了
口胡一个方程
看似正确
实际上这个方程会重复统计,设对于一个点,所有与他有连接且在\(S\)内的点的集合为\(pi\)
若\(pi\)属于\(s\),那么在dp过程中,就会记重,比如
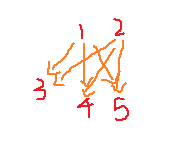
我们沿用上面\(s,t\)的状态解释,若\(s\)={1,2},\(t\)={4,5},当我们用这种状态,显然我们只会添加\(3\)
但是新的状态才不会管你这么多,\(4,5\)照样有可能被添加,那么我们就记重了
于是怎么办,若\(pi\)属于\(s\),那么设\(s\)下面挂着的节点个数是\(cs\)个
所以在\(dp_{s',t}\)的基础上,我们新添加一个点有\(cs-t\)种选择
所以总结下方程
最后累乘的时候还要考虑一个问题,若一个序列长度为\(x\)另一个为\(y\),两个序列是可以交叉的
所以还要乘上组合数\(C_{x+y}^{x}\),来统计交叉的情况,实际写下来就是\(C_{\sum{len}+x}^{x}\)
光说可能还是很玄幻,可以看代码:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<vector>
#include<algorithm>
#define ll long long
#define P peach//纯属好玩
using namespace std;
const ll mod=1e9+7;
ll n,m,a[401],f[1<<15][71],g[1<<15],fa[10001],in[1001],c[201][201];
ll peach[1<<15],ans=1,hd=0;
vector<ll>vec[101],Vec;
ll g_fa(ll x){//不需要分层,于是并查集很香
if(fa[x]==x)return x;
else return g_fa(fa[x]);
}
int main(){
scanf("%lld",&n);
for(ll i=1;i<=n;i++)scanf("%lld",&a[i]);
sort(1+a,1+a+n);
for(ll i=1;i<=n;i++)fa[i]=i;
for(ll i=1;i<=n;i++){
for(ll j=i+1;j<=n;j++){
if(a[j]%a[i]==0){
ll t1=g_fa(i),t2=g_fa(j);
in[j]++;
if(t1!=t2)fa[t2]=t1;
}
}
}
c[0][0]=c[0][1]=c[1][1]=1;
for(ll i=2;i<=2*n;i++){
c[0][i]=1;
for(ll j=1;j<=i;j++)c[j][i]=(c[j-1][i-1]+c[j][i-1])%mod;
}
for(ll i=1;i<=n;i++){
vec[g_fa(i)].push_back(i);
}
for(ll i=1;i<=n;i++){
if(vec[i].size()>1){
Vec.clear();
for(ll j=0;j<vec[i].size();j++){
if(in[vec[i][j]]==0)Vec.push_back(vec[i][j]);
}
ll N=1<<Vec.size(),cnt=0;
memset(g,0,sizeof g),memset(f,0,sizeof f);
for(ll j=0;j<vec[i].size();j++){
if(in[vec[i][j]]){
cnt++;
for(ll k=0;k<Vec.size();k++){
if(a[vec[i][j]]%a[Vec[k]]==0)P[vec[i][j]]|=1<<k;
}
g[P[vec[i][j]]]++;
}
}
for(ll j=0;j<Vec.size();j++){
for(ll k=0;k<N;k++){
if(k>>j&1)g[k]+=g[k-(1<<j)];
}
}
f[0][0]=1;
for(ll j=0;j<N;j++){
for(ll k=0;k<=cnt;k++){
if(f[j][k]){
if(k<g[j])f[j][k+1]=(f[j][k+1]+f[j][k]*(g[j]-k)%mod)%mod;
for(ll p:vec[i]){
if(in[p]&&((P[p]&j)!=P[p])&&((P[p]&j)||j==0)){
f[j|P[p]][k+1]=(f[j|P[p]][k+1]+f[j][k])%mod;
}
}
}
}
}
ans=ans*f[N-1][cnt]%mod*c[cnt-1][hd+cnt-1]%mod;
hd+=cnt-1;
}
}
cout<<ans;
}


