单调队列DP->斜率DP

蒟蒻题单

瑰丽华尔兹

考虑到知识点是单调队列，考虑怎么使用单调队列
首先说明一点，小天使可以选择当前时刻钢琴是否移动（并非一次就要一段时间）
考虑DP方程，由于每次只能走一个方向，选择不了，其实就相当于一个一维的DP了
以往上(北)为例(t为第t段时间)

\[f[t][i][j]=max_{f[t-1][i'][j]+(i-i')} \]

\[变形为 \]

\[f[t][i][j]=max_{f[t-1][i'][j]-i'}+i \]

然后把\(f[t-1][i'][j]-i'\) 扔进单调队列里就可以
然后代码没事找事用了提前声明,不太好看

#include<iostream>
#include<cstdio>
#include<cstring>
#define ll long long
using namespace std;
ll xx,yy,n,m,t,f[300][300],dx[5]={0,-1,1,0,0},dy[5]={0,0,0,-1,1},ans;
char c[300][300];

struct dequeue{
	ll pos,ff;
}q[100001];

void dp(ll x,ll y,ll d,ll len);

int main(){
	memset(f,-0x3f,sizeof f);
	scanf("%lld%lld%lld%lld%lld",&n,&m,&xx,&yy,&t);
	for(ll i=1;i<=n;i++){
		char dc=getchar();
		for(ll j=1;j<=m;j++){
			c[i][j]=getchar();
		}
	}
	f[xx][yy]=0;
	while(t--){
		ll T,S,D,L;
		scanf("%lld%lld%lld",&S,&T,&D);
		L=(T-S+1);
		if(D==1)for(ll i=1;i<=m;i++)dp(n,i,D,L);
		if(D==2)for(ll i=1;i<=m;i++)dp(1,i,D,L);
		if(D==3)for(ll i=1;i<=n;i++)dp(i,m,D,L);
		if(D==4)for(ll i=1;i<=n;i++)dp(i,1,D,L);
	}
	cout<<ans;
}

void dp(ll x,ll y,ll d,ll len){
	ll l=1,r=0;
	for(ll i=1;x<=n&&y<=m&&x>=1&&y>=1;x+=dx[d],y+=dy[d],i++){
		if(c[x][y]=='x')l=1,r=0;
		else {
			while(l<=r&&q[r].ff+i-q[r].pos<f[x][y])r--;
			q[++r]=dequeue{i,f[x][y]};
			while(i-q[l].pos>len)l++;
			f[x][y]=q[l].ff+i-q[l].pos;
			ans=max(ans,f[x][y]);
		}
	}
}

很好，咕了一年，让我们继续

火星藏宝图

题目
首先，\(n^2\)的做法不难想
暴力枚举现在的点，然后枚举决策点 \(f_i=min(f_j-dis_{ij}+w_{ij})\)
然后考虑优化
这里有个有意思的贪心：

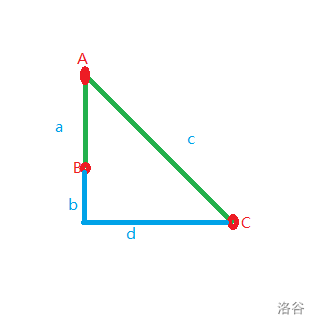
考虑题意，\(A C\)点间距离为\(c^2=(a+b)^2+d^2\)稍作计算就会发现直接走\(A C\)不如顺便去一下\(B\)
所以对于每一列，最下面的点必定是最优的（不要忘了\(w\)大于零）
用一个\(st\)数组记录下每一列的最优点在第几排，设\(f_{ij}\)表示走到第\((i,j)\)点的最大收获

\[f[i][j]=min(f[st[k]][k]-dis(i,j,st[k],k)+w[i][j]) \]

时间复杂度变成了\(m^3\)
意识到可以用下单调队列优化一下
先无视掉第一维，设\(i\)为当前列
设：

\[dis_{j}=(i-st[j]) \]

\[f[i]=min(f[j]-dis[j]-(i-j)^2)+w[i] \]

若第\(j\)列优于第\(k\)列

\[f[j->i]>f[k->i] \]

\[f[j]-dis[j]-i^2+2*ij-j^2>f[k]-dis[k]-i^2+2*ik-k^2 \]

\[f[j]-f[k]-dis[j]+dis[k]-j^2+k^2>2i*(k-j) \]

\[\frac{f[j]-f[k]-dis[j]+dis[k]-j^2+k^2}{2*(k-j)}>i \]

显然是斜率\(DP\)格式，后面就直接套"模板"

#include<iostream> 
#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
#define ld long double 
using namespace std;
const ld eps=1e-6;
const ll M=2100;
ll n,m,f[M][M],st[M],w[M][M],q[M],l,r,dis[M];

ll disc(ll x,ll y){
	return (x-y)*(x-y);
}

ld K(ll x,ll y){
	if(x!=y)return (f[st[x]][x]-dis[x]-x*x-f[st[y]][y]+dis[y]+y*y)/(y-x)/2.0;
	return -1e9;//这点不要忘记
}

int main(){
	memset(f,-0x3f,sizeof(f));
	scanf("%lld%lld",&n,&m);
	for(ll i=1,a1,a2,a3;i<=n;i++){
		scanf("%lld%lld%lld",&a1,&a2,&a3);
		w[a1][a2]=a3;
	}
	f[1][1]=w[1][1],st[1]=1;
	w[1][1]=0;
	for(ll i=1;i<=m;i++){
		l=1,r=0;
		for(ll j=1;j<=m;j++){
			dis[j]=(st[j]!=0)*disc(st[j],i);
		}
		for(ll j=1;j<=m;j++){
			if(st[j]){
				while(l<r&&K(q[r-1],q[r])>K(q[r],j))r--;
				q[++r]=j;
			}
			if(w[i][j]){
				while(l<r&&K(q[l],q[l+1])<j)l++;
				f[i][j]=f[st[q[l]]][q[l]]-dis[q[l]]-disc(j,q[l])+w[i][j];
				st[j]=i,dis[j]=0;//不要忘记dis赋为零
				while(l<r&&K(q[r-1],q[r])>K(q[r],j))r--;
				q[++r]=j;
			}
		}
	}
	cout<<f[m][m];
}