合并排序
根据网络博客教程修改而来。
合并排序，就是通过将两个有序的序列合并为一个大的有序序列的方式来实现排序。合并排序是一种典型的分治算法：首先将序列分为两部分，然后对每一部分进行循环递归的排序，然后逐个将结果进行合并。如下：
A. 分解，将待排序元素分成大小大致相同的两个子序列。
B. 求解子问题，用合并排序法分别对两个子序列递归的进行排序。
C. 合并，将排好序的有序子序列进行合并，得到符合要求的有序序列。
合并排序依赖于合并操作，即将两个已经排序的序列合并成一个序列，具体的过程如下：
- 申请空间，使其大小为两个已经排序序列之和，然后将待排序数组复制到该数组中
- 设定两个指针，最初位置分别为两个已经排序序列的起始位置
- 比较复制数组中两个指针所指向的元素，选择相对小的元素放入到原始待排序数组中，并移动指针到下一位置
- 重复步骤3直到某一指针达到序列尾
- 将另一序列剩下的所有元素直接复制到原始数组末尾
合并的过程和方法：
设置三个工作指针i，j，k，其中i和j指向两个待排序序列中当前需要比较的两个元素，k指向辅助数组B中待放置元素的位置。比较A[i]和A[j]的大小关系，如果A[i]<A[j]，则B[k]=A[i]，同时将指针i和k分别推进一步；反之，B[k]=A[j]，同时将指针j和k分别推进一步。如此反复，直到其中的一个序列为空。最后，将非空序列中的剩余元素按原次序全部放到辅助数组B的尾部。
伪码描述如下：
void merge(int a[], int low, int high) {
int i, j, k;
int *B = new int [high-low+1];
int mid = low + (high-low) / 2;
i = low; j = mid + 1; k = 0;
while(i <= mid && j <=high) { // 两个子序列非空，将较小的一个移到B中
if (a[i] < a[j]) B[k++] = a[i++];
else B[k++] = a[j++];
while(i <= mid) B[k++] = a[i++]; // 将非空序列中的剩余元素放到B尾部
while(j <= high) B[k++] = a[j++];
for (k=0, i=low; i <= high; i++, k++) a[i] = B[k]; // 将B中0～（high-low)复制到a中low～high
}
这样，合并排序的伪代码描述为：
void mergeSort(int a[], int low, int high) {
if (low >= high) return;
int middle = (high + low) / 2;
mergeSort(a, low, middle);
mergeSort(a, middle + 1, high);
merge(a, low, high);
}
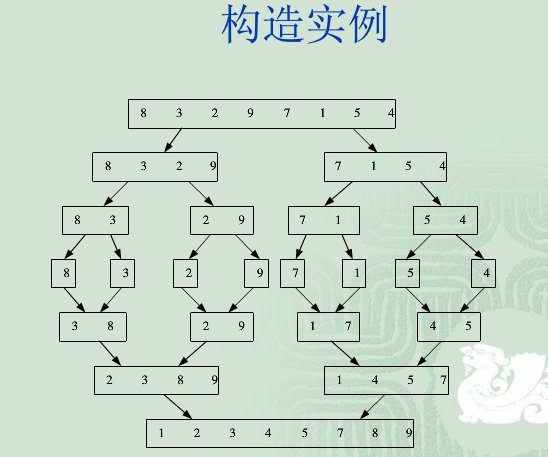
实例运行过程如图示：
