数据结构——排序
排序算法的评价指标
-
时间复杂度
-
空间复杂度
-
稳定性:排序表中相同的两个元素经过该排序算法时无论怎样,排序后这两个元素的相对位置始终没有变化,则称这个排序算法是稳定的;否则为不稳定的。
(稳定算法不一定比不稳定的算法好)
排序算法的分类
- 内部排序:数据都在内存中。(注重更低的时间、空间复杂度)
- 外部排序:数据量太大,无法全部放入内存中。(重更低的时间、空间复杂度的同时,还要注重磁盘的读写次数)
内部排序
插入排序
直接插入排序
时间复杂度:
- 最坏\(O(n^2)\);
- 最好\(O(n)\);
- 平均\(O(n^2)\)
空间复杂度:\(O(1)\)
稳定
算法思想
每次将扫描到的元素插入到前面已经排好序的子序列中
代码样例
//由小到大排序
void Insert_Sort(int num[],int n){
for(int i=1 ;i < n; i++){
if(num[i] < num[i-1]){
int temp = num[i];
int j;
for(j = i-1; j >= 0; j--){
if(temp < num[j]){
num[j+1] = num[j];
}
else{
break;
}
}
num[j+1] = temp;
}
}
}
折半插入排序
- 时间复杂度:
- 最坏\(O(n^2)\);
- 最好\(O(n)\);
- 平均\(O(n^2)\)
算法思想
直接插入排序的优化,利用折半查找找出需要插入元素的位置。同时为保证算法稳定性,当mid值等于要插入元素的值时应继续执行折半查找的算法(一从小到大为例使\(low=mid+1\))直到\(low>high\)为止,之后将其插入到low位置即可。
代码样例
//由小到大排序
void Half_Insert_Sort(int num[],int n){
for(int i=1 ;i < n; i++){
if(num[i] < num[i-1]){
int temp = num[i];
int low = 0,high = i-1, mid;
while(low <= high){
mid = (low+high)/2;
if(num[mid] >= temp)
high = mid - 1;
else{
low = mid + 1;
}
}
for(int j = i-1; j >= low; j--){
num[j+1] = num[j];
}
num[low] = temp;
}
}
}
链表的插入排序
- 时间复杂度:
- 最坏\(O(n^2)\);
- 最好\(O(n)\);
- 平均\(O(n^2)\)
减少了查找后移动的步骤
代码样例
//由小到大排序
void LinkList_Insert_Sort(LinkList *L){
Node *p,*r,*s;
*p = L->next;
while(p->next != NULL){
*r = p->next;
if(r->data < p->data){
p->next = r->next;
*s = L;
while(s->next->data <= r->data){
s = s->next;
}
r-next = s->next->data;
s->next = r;
}
}
}
希尔排序
时间复杂度:无法用数学确切证明
- 最坏当间距等于1时退化为直接插入排序\(O(n^2)\);
- 当
n在某一个范围内为\(O(n^{1.3})\)空间复杂度:\(O(1)\)
不稳定,仅适用于顺序表
算法思想
将排序的列表每次以某间距组成新的子表,在各自的子表内进行直接排序。其中每次间隔不断减小(如间隔为上次间隔的一半)
代码样例
//由小到大排序
void Shell_Sort(int num[],int n){
for(int d = n/2; d >= 1; d/=2){
for(int i = d; i < n; i++){//为了便于实现代码,每次对子表两个位置进行插入排序,之后对下一个子表相应位置进行插入排序
cout << i << endl;
if(num[i-d] > num[i]){
int temp = num[i];
int j;
for(j = i-d; j >= 0; j-=d){
if(temp < num[j]){
num[j+d] = num[j];
}
else{
break;
}
}
num[j+d] = temp;
}
}
}
}
交换排序
冒泡排序
时间复杂度:
- 最好\(O(n)\);
- 最坏\(O(n^2)\)
空间复杂度:\(O(1)\)
稳定
算法思想
从到尾或者从尾到头两两相互比较交换位置
代码样例
//由小到大排序,大的往后冒
void Bubble_Sort(int num[],int n){
for(int i=0; i < n-1; i++){
for(int j=0; j < n-1; j++){
if(num[j+1] < num[j]){
int temp = num[j];
num[j] = num[j+1];
num[j+1] = temp;
}
}
}
}
★★★快速排序
时间复杂度:\(O({n}\times{递归层数})\);把每次递归调用依次列出来可以看到是一个二叉树,所以\(递归层数=二叉树高度\)
- 最坏(左右划分不均匀)\(O(n^2)\);
- 最好(左右划分不均匀)\(O(nlog_{2}n)\)
- 平均(左右划分不均匀)\(O(nlog_{2}n)\)
空间复杂度:\(O(递归层数)\);
- 最坏(左右划分不均匀)\(O(n)\)
- 最好(左右划分均匀)\(O(log_{2}{n})\)
不稳定
算法思想
以某一数为基准,将比基数基数大和比基数小的分别放在基数两边。之后对左右两边的子序列递归调用该方法
代码样例
void Quick_Sort(int num[], int left, int right){
if(left >= right)
return;
int temp=num[left];
int i = left;
int j = right;
while(i != j){
while(temp <= num[j] && i < j){
j--;
}
while(temp >= num[i] && i < j){
i++;
}
if(i < j){
int t = num[i];
num[i] = num[j];
num[j] = t;
}
}
//基准数归位
num[left] = num[i];
num[i] = temp;
Quick_Sort(num,left,i-1);//递归调用
Quick_Sort(num,i+1,right);
}
选择排序
简单选择排序
时间复杂度:\(O(n^2)\)
空间复杂度:\(O(1)\)
不稳定
算法思想
在待排序序列中每次找到最小(或最大)的元素放在有序的序列中
代码样例
void Simple_Select_Sort(int num[], int n){
for(int i=0; i < n-1; i++){
int min_pos = i;
for(int j=i+1; j < n; j++){
if(num[j] < num[min]){
min_pos = j
}
}
if(min != i){
int temp = num[i];
nun[i] = num[min_pos];
num[min_pos] = temp;
}
}
}
★★★堆排序
时间复杂度:\(O(nlog_{2}{n})\)
空间复杂度:\(O(1)\)
不稳定
算法思想
同简单选择排序,但其通过堆来实现。
堆细分为大根堆和小根堆,在逻辑上是完全二叉树的顺序存储。其中大根堆即\({根节点}\ge{左、右子节点}\);小根堆即\({根节点}\le{左、右子节点}\)。
堆排序Heap_Sort具体分为三部:
-
第一步:建立初始堆
Build_Heap。 -
第二步:交换根节点与最后元素的位置
Swap。 -
第三步:维护堆
Heapify。
大根堆得到的为递增序列,小根堆得到的是递减序列。
代码样例
//从小到大排序,建立大根堆
void Swap(int i,int j){
int temp = i;
i = j;
j = temp;
}
void Heapify(int num[], int n; int i){
if(i >= n){
return ;
}
int c1 = 2 * i + 1;
int c2 = 2 * i + 2;
int max_pos = i;
if(num[c1] > num[max] && c1 < n){
max_pos = c1;
}
if(num[c2] > num[max] && c2 < n){
max_pos = c2;
}
if(max != i){
Swap(num[max],num[i]);
Heapify(num,n,max);
}
}
void Build_Max_Heap(int num[],int n){
int last_node = n-1;
int parent = (last_node - 1)/2;
for(int i=parent; i >= 0; i--){
Heapify(int num, int n, int i)
}
}
void Heap_Sort(int num,int n){
Build_Max_Heap(num,n);
for(int i=n-1; i >= 0; i--){
Swap(num[i],num[0]);
Heapify(num, i, 0);
}
}
堆的插入和删除
向堆中插入新元素时,应插入到堆底后面;
删除元素时,需要将堆底最后一项移动到删除的位置上。
归并排序(二路归并排序)
时间复杂度:归并树是倒立二叉树
- \(O(nlog_{2}{n})\)
空间复杂度:主要来自于辅助数组
- \(O(n)\)
稳定
算法思想
把两个或者多个已经有序的序列合成一个有序的序列
代码样例
int *temp_num = (int *)malloc(n*sizeof(int));
void Merge(int num,int left, int mid, int high){
int i,j,k;
for(k=low; k <= high; k++){
temp_num[k] = num[k];
}
for(i=low, j=mid+1,k=left; i <= mid && j <= right; k++){
if(temp_mun[i] <= temp_num[k]){
num[k] = temp_num[i++];
}else{
num[k] = temp_num[j++];
}
}
while(i <= mid){
num[k++]=temp_num[i++];
}
while(j <= right){
num[k++]=temp_num[j++];
}
}
void Merge_Sort(int num[], int left,int right){
if(left < right){
int mid = (left+right)/2;
Merge_Sort(num,left,mid);//左边递归调用
Merge_Sort(num,mid+1,right);//右边递归调用
Merge(num,left,mid,right);左右两路进行归并
}
}
更多路见下文外部排序中的K路归并排序
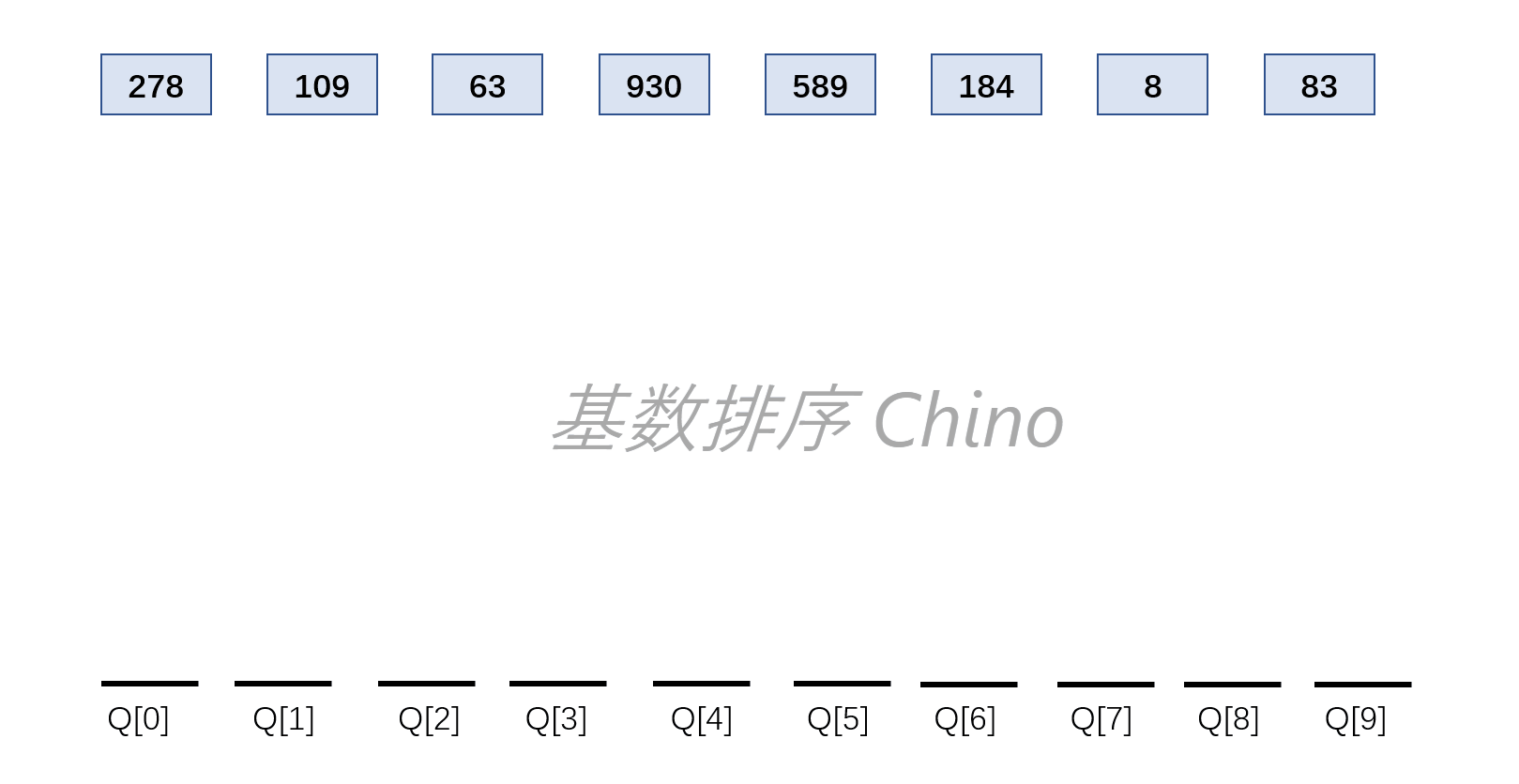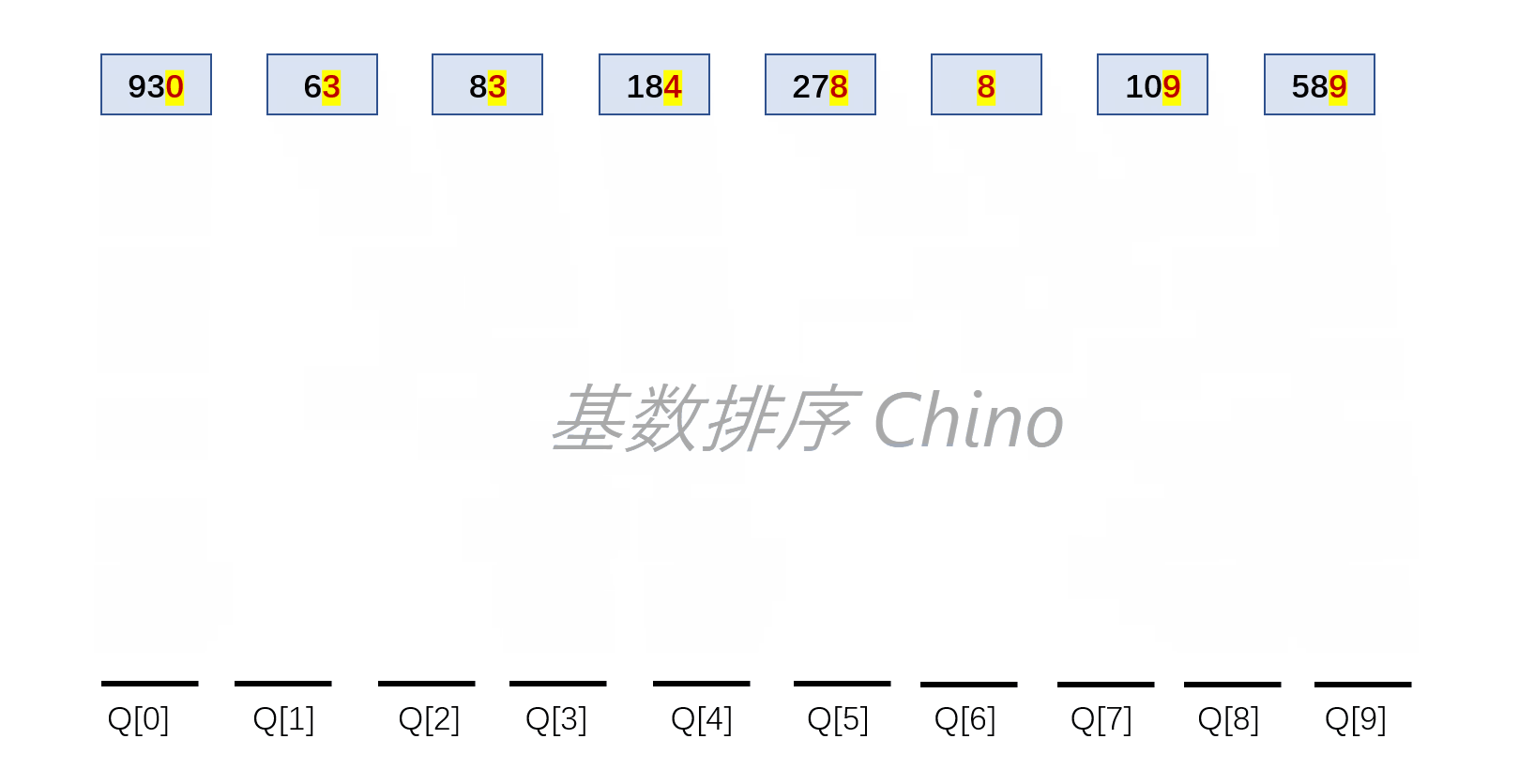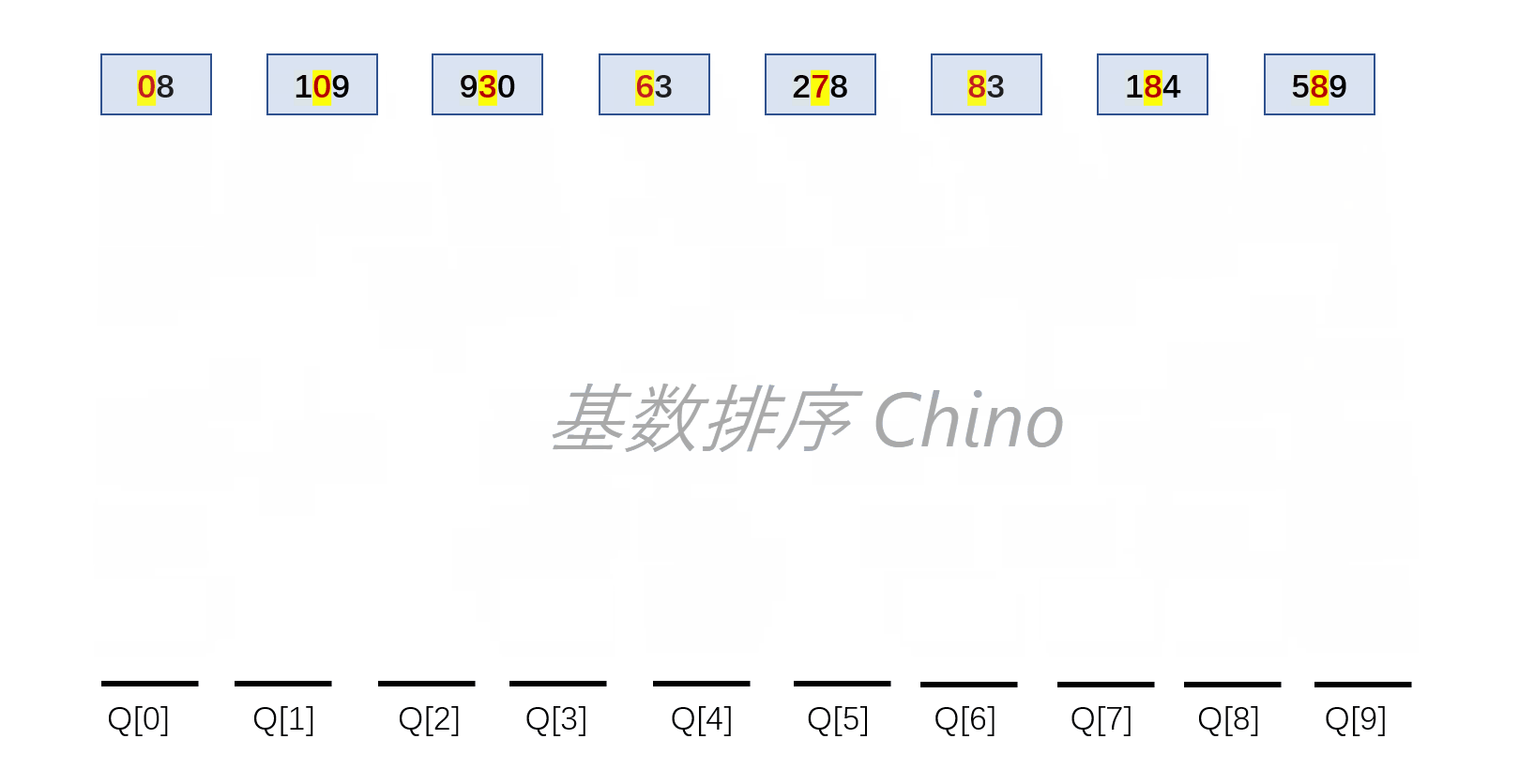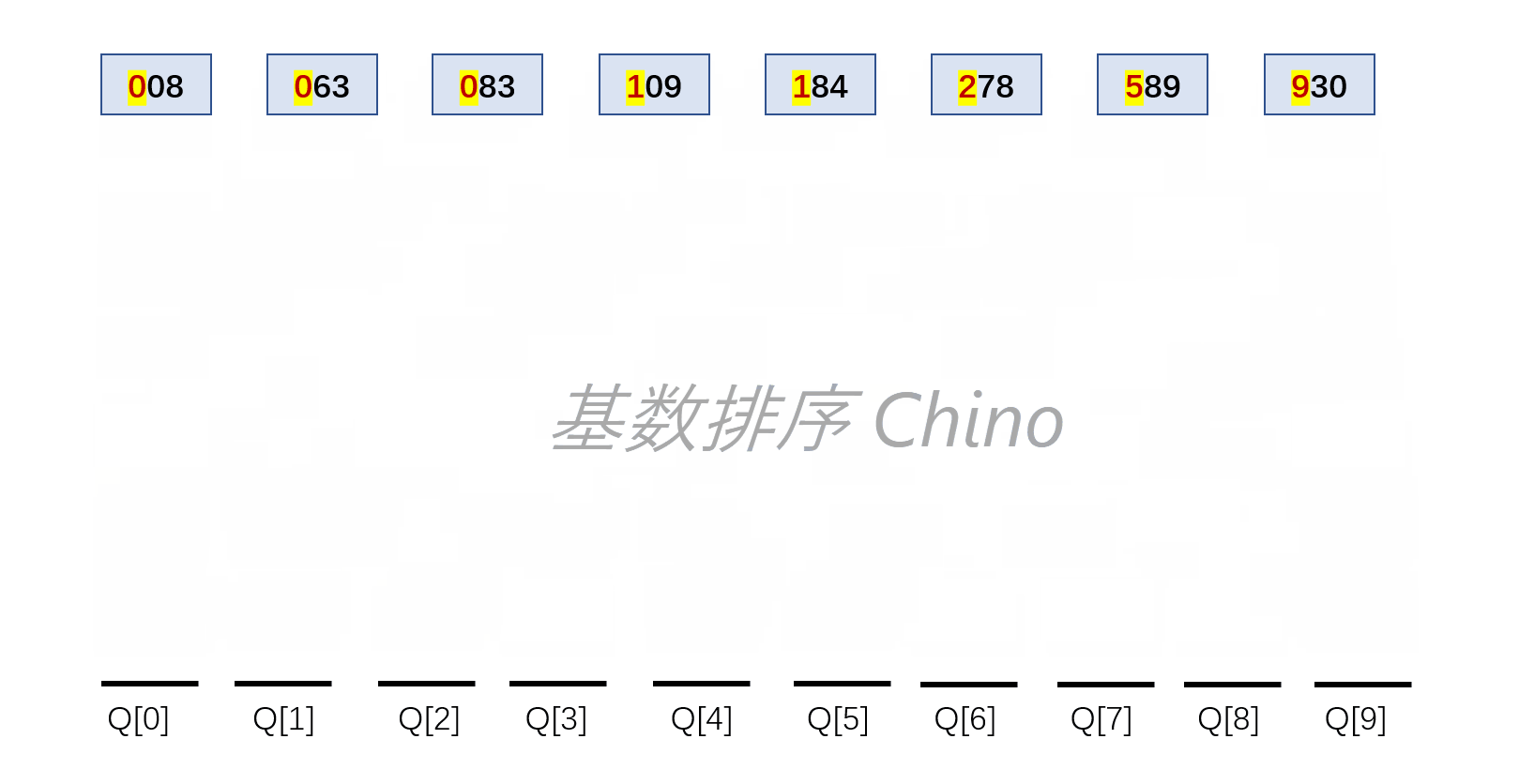
基数排序
时间复杂度:
- \(O(d\times(n+r))\)
空间复杂度:
- \(O(r)\)
稳定
算法思想
将待排序元素的关键字拆成d组,之后根据关键字做d躺的“分配”和“收集”
- 适合用于:
- 数组元素的关键字可以方便拆分成
d组,且d比较小; - 待排序元素
n比较大; - 每组关键字的范围
r比较小;
- 数组元素的关键字可以方便拆分成
见下图例子