（补题 POJ 3013） Big Christmas Tree

原题链接戳我~

题目描述

给你一个图，每个顶点和边都有权值。问能否构建出一棵树，如果能，请计算出代价最小的方案，如果不能请输出"-1"

代价的计算方法：所有边（该边的所有子节点的和\(\times\)该边的权值）的和（语文不好233333，只能解释到这了看不懂请看下面解题思路的样例~）

Sample Input

2
2 1
1 1
1 2 15
7 7
200 10 20 30 40 50 60
1 2 1
2 3 3
2 4 2
3 5 4
3 7 2
3 6 3
1 5 9

Sample Output

15
1210

解题思路

最短路+注意数据过大以及INF需要开到超过0x3f3f3f3f

我们就拿样例中的第二组数来推导一下公式

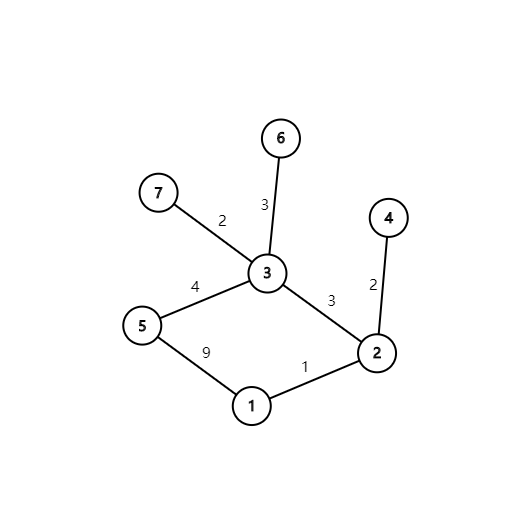
通过样例我们不难看出，只需要删除1号点与5号点之间的9这条边然后进行建树 （如下图）

\(1\times(60+40+50+20+30+10)+2\times30+3\times(40+60+50)+4\times40+2\times60+3\times50\)

经过整理可得出（下角标为对应的节点编号）

\(60_{(7)}\times(1+3+2)+40_{(5)}\times(1+3+4)+50_{(6)}\times(1+3+3)+20_{(3)}\times(1+3)+30_{(4)}\times(1+2)+10_{(2)}\times1+200_{(1)}\times0\)

不难看出权值为每个店点到根节点1的最短路径乘上这个点的权值，加下来就要套用最短路的板子了，这个地方的最短路我用的是SPFA

代码样例

#include<cstdio>
#include<cstring>
#include<stack>
#include<queue>

#define INF 1E16
using namespace std;

typedef long long ll;
bool visit[50005];
ll d[50005];
int head[50005];
int N,M;
int aa[50005];

struct node{
	int x,w,next;
}edge[150005];
int cnt = 0;
void add ( int u, int v, int w ) {
	edge[cnt].x = v, edge[cnt].w = w, edge[cnt].next = head[u]; head[u] = cnt++; 
}

void spfa()
{
	int i,k;
	queue<int>S;
	while(!S.empty())
	S.pop(); 
	memset(visit,0,sizeof(visit));
	for(i=2;i<=N;i++) d[i]=INF;
	d[1]=0;
	S.push(1);
	visit[1]=1;
	while(!S.empty()){
		k=S.front();
		S.pop();
		visit[k]=0;
		for(i=head[k]; i!=-1; i=edge[i].next){
			if(d[edge[i].x]>edge[i].w+d[k]){
				d[edge[i].x]=edge[i].w+d[k];
				if(!visit[edge[i].x]){
					S.push(edge[i].x);
					visit[edge[i].x]=1;
				}
			}
		}
	}
	int flag = 0;
	for(i = 1; i <= N; i++){
		if(d[i] == INF){
			flag = 1;
			break;			
		}
	}
	if(flag == 1){
		printf("No Answer\n");
	}
	else{
		ll sum = 0;
		for(i = 1; i <= N; i++){
			sum += d[i]*aa[i];
		}
		printf("%lld\n",sum);
	}     
}

int main()
{
	int T,x,w,v,i;
	scanf("%d",&T);
	while(T--){		
		scanf("%d %d",&N,&M);
		memset(head,-1,sizeof(head));
		
		for(i = 1; i <= N; i++){
			scanf("%lld",&aa[i]);
		}

		cnt = 0;
		for ( i = 1; i <= M; i++ ) {
			scanf("%d%d%d",&x,&w,&v);
			add( x, w, v );
			add( w, x, v );
		}

		// for(i=1;i<=M;i++){
		// scanf("%d%d%d",&x,&w,&v);
		// // edge[i].x = w, edge[i].w = v, edge[i].next = head[x]; head[x] = i; 
		// // edge[i].x=w;
		// // edge[i].w=v;
		// // edge[i].next=head[x];
		// // head[x]=i;
		// }

		spfa();
	}
return 0;
}