最短路问题
*加载本页面时,公式可能未渲染(显示乱码)请刷新该页面重试
单源最短路
Dijkstra算法(不带负权,单源最短路)
(这里干讲不好说,所以直接上模板题来分析一下)
时间复杂度\(O(N^2)\)(朴素)\(O((M+N)logN)\)(优化后)
空间复杂度\(O(M)\)
与最小生成树中的Prime算法大体相同,注意区分这两个算法
模板题
[1] POJ-2387 Til the Cows Come Home
Description
Bessie is out in the field and wants to get back to the barn to get as much sleep as possible before Farmer John wakes her for the morning milking. Bessie needs her beauty sleep, so she wants to get back as quickly as possible.
Farmer John's field has N (2 <= N <= 1000) landmarks in it, uniquely numbered 1..N. Landmark 1 is the barn; the apple tree grove in which Bessie stands all day is landmark N. Cows travel in the field using T (1 <= T <= 2000) bidirectional cow-trails of various lengths between the landmarks. Bessie is not confident of her navigation ability, so she always stays on a trail from its start to its end once she starts it.
Given the trails between the landmarks, determine the minimum distance Bessie must walk to get back to the barn. It is guaranteed that some such route exists.
Input
* Line 1: Two integers: T and N
* Lines 2..T+1: Each line describes a trail as three space-separated integers. The first two integers are the landmarks between which the trail travels. The third integer is the length of the trail, range 1..100.
Output
* Line 1: A single integer, the minimum distance that Bessie must travel to get from landmark N to landmark 1.
Sample Input
5 5
1 2 20
2 3 30
3 4 20
4 5 20
1 5 100
Sample Output
90
Hint
INPUT DETAILS:
There are five landmarks.
OUTPUT DETAILS:
Bessie can get home by following trails 4, 3, 2, and 1.
分析
测试样例转化成图(如下)
.png)
我们先将二维数组初始化为最大值(INF),然后存入图。在程序中图的二维数组存储如下
| 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1 | 0 | 20 | ∞ | ∞ | ∞ |
| 2 | ∞ | 0 | 30 | ∞ | ∞ |
| 3 | ∞ | ∞ | 0 | 20 | ∞ |
| 4 | ∞ | ∞ | ∞ | 0 | 20 |
| 5 | 100 | ∞ | ∞ | ∞ | 0 |
接下来用vis这个数组来标记知道最短路的点(如果为最短路就标记为1,否则为0),先把dis数组里面全部初始化为从1点到相应点的距离每次用如下代码判断是否为最短路如果不是则更新最短距离
for(int j=1; j <= n; j++){
if(dis[te]+map_[te][j] < dis[j] && vis[j] == 0)
dis[j]=dis[te]+map_[te][j];
}
代码样例
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <clocale>
using namespace std;
const int maxn=2005,inf=0x3f3f3f3f;
int t,n;
int map_[maxn][maxn],dis[maxn],vis[maxn];
void Dijkstra(){
memset(vis,0,sizeof(vis));
memset(dis,0,sizeof(dis));
for(int i=1; i <= n; i++)
dis[i] = map_[1][i];
for(int i=1; i <= n; i++){
int mi=inf,te;
for(int j=1; j <= n; j++)
if(vis[j] == 0 && dis[j] < mi){
mi=dis[j];
te=j;
}
vis[te]=1;
for(int j=1; j <= n; j++){
if(dis[te]+map_[te][j] < dis[j] && vis[j] == 0)
dis[j]=dis[te]+map_[te][j];
}
}
cout << dis[n] << endl;
}
int main() {
cin >> t >> n;
// memset(map_,-1,sizeof(map_));
for(int i=1; i <= n; i++)
for(int j=1; j <= n; j++){
if(i == j)
map_[i][j]=0;
else
map_[i][j]=map_[j][i]=inf;
}
for(int i=1; i <= t; i++) {
int from, to, val;
cin >> from >> to >> val;
if(map_[from][to] > val)
map_[from][to]=map_[to][from]=val;
}
Dijkstra();
return 0;
}
Bellman-Ford算法(负权)
这个思路相对于这里面中最简单的了同时适用范围也很广(就是效率有点低,时间复杂度较高)。
时间复杂度\(O(M)\)
空间度杂度\(O(MN)\)
思路
核心代码
for(int i=1; i <= m; i++)
if(dis[v[i]] > dis[u[i]] + w[i])
dis[v[i]] = dis[u[i]] + w[i];
(代码中u[i],v[i],w[i]分别表示第i条边的起点,终点,距离)上述代码意思为看看能否通过u[i]->v[i] (权值为w[i]),使得1号顶点到v[i]号顶点的距离变短(同松弛)。
判环应用
每松弛一次时把每条边都更新一下,所以在没有形成回路的条件下n个点进行n-1次松弛后就完成了最短路的寻找(本思路还以判断是否形成环路,下面我只放了可以用这种思路实现的例题)。
模板题
[1] POJ-3259 Wormholes
虫洞是很奇特的,因为它是一个单向通道,可让你进入虫洞的前达到目的地!他的N(1≤N≤500)个农场被编号为1..N,之间有M(1≤M≤2500)条路径,W(1≤W≤200)个虫洞。FJ作为一个狂热的时间旅行的爱好者,他要做到以下几点:开始在一个区域,通过一些路径和虫洞旅行,他要回到最开时出发的那个区域出发前的时间。也许他就能遇到自己了:)。为了帮助FJ找出这是否是可以或不可以,他会为你提供F个农场的完整的图(1≤F≤5)。所有的路径所花时间都不大于10000秒,所有的虫洞都回到不大于10000秒之前。
Input
第1行:一个整数F表示接下来会有F个农场说明。 每个农场第一行:分别是三个空格隔开的整数:N,M和W 第2行到M+1行:三个空格分开的数字(S,E,T)描述,分别为:需要T秒走过S和E之间的双向路径。两个区域可能由一个以上的路径来连接。 第M +2到M+ W+1行:三个空格分开的数字(S,E,T)描述虫洞,描述单向路径,S到E且回溯T秒。
Output
F行,每行代表一个农场 每个农场单独的一行,” YES”表示能满足要求,”NO”表示不能满足要求。
Sample Input
2
3 3 1
1 2 2
1 3 4
2 3 1
3 1 3
3 2 1
1 2 3
2 3 4
3 1 8
Sample Output
NO
YES
Hint
For farm 1, FJ cannot travel back in time.
For farm 2, FJ could travel back in time by the cycle 1->2->3->1, arriving back at his starting location 1 second before he leaves. He could start from anywhere on the cycle to accomplish this.
解题思路
模板题,松弛一遍然后再从头找一遍(相同点的时间为0)看能否还还有让时间变得更短的路径如果有则说明存在;否则说明不存在。
代码样例
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
using namespace std;
const int maxn=(int)1e4+5;
const int inf=0x3f3f3f3f;
struct node{
int s,e,t;
}edge[maxn];
int n,m,w,cont;
int dis[maxn];
bool bellman() {
memset(dis, inf, sizeof(dis));
dis[1] = 0;
int oj;
for (int i = 1; i < n; i++) {
oj = 0;
for (int j = 0; j < cont; j++) {
int u,v,w;
u=edge[j].s;
v=edge[j].e;
w=edge[j].t;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
oj = 1;
}
}
if (oj == 0)
break;
}
for (int j = 0; j < cont; j++){
int u,v,w;
u=edge[j].s;
v=edge[j].e;
w=edge[j].t;
if (dis[v] > dis[u] + w)
return true;
}
return false;
}
int main(){
int f;
cin >> f;
while(f--) {
cont=0;
cin >> n >> m >> w;
for(int i=1; i <= m; i++) {
int ts, te, tt;
cin >> ts >> te >> tt;
edge[cont].s =ts;
edge[cont].e =te;
edge[cont].t =tt;
cont++;
edge[cont].s =te;
edge[cont].e =ts;
edge[cont].t =tt;
cont++;
}
for(int i=1; i <= w; i++){
int ts, te, tt;
cin >> ts >> te >> tt;
edge[cont].s =ts;
edge[cont].e =te;
edge[cont].t =-tt;
cont++;
}
if(bellman())
cout << "YES" << endl;
else
cout << "NO" << endl;
}
return 0;
}
SPFA算法(队列优化的Bellman-Ford算法)
时间复杂度(最坏打算)\(O(NM)\)
空间复杂度\(O(M)\)
思路
Bellman-Ford算法上文中我们提及了其算法的复杂度比较高,原因是我们不管点的最短路是否发生了变化都将它们松弛一下,现在想上去里面一些不必要的过程——只对最短路发生了变化的点进行松弛操作。本算法就是这种优化的一个方法,即用一个队列来记录那些最短路发上变化的点。
在原来的算法上加入队列,每次选队首的点u,对顶点u的所有出边进行松弛操作。假设有u,v比原来录入的距离短且v不在队列里面(用一个数组来判断知否重复),就把v放在队尾。直到u的所有出边松弛完毕后将u移除队列,然后多次循环。
举个数据样例
5 7
1 2 2
1 5 10
2 3 3
2 5 7
3 4 4
4 5 5
5 3 6
来一个图
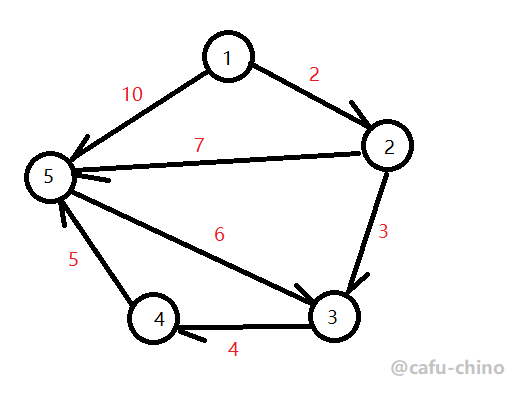
我们仍然用dis这个数组来保存1顶点到各个点的距离,初始时dis[1]=1,其余为无穷大。接下来将1这个点入队

接着是1->2找最小距离,2入队

依次进行
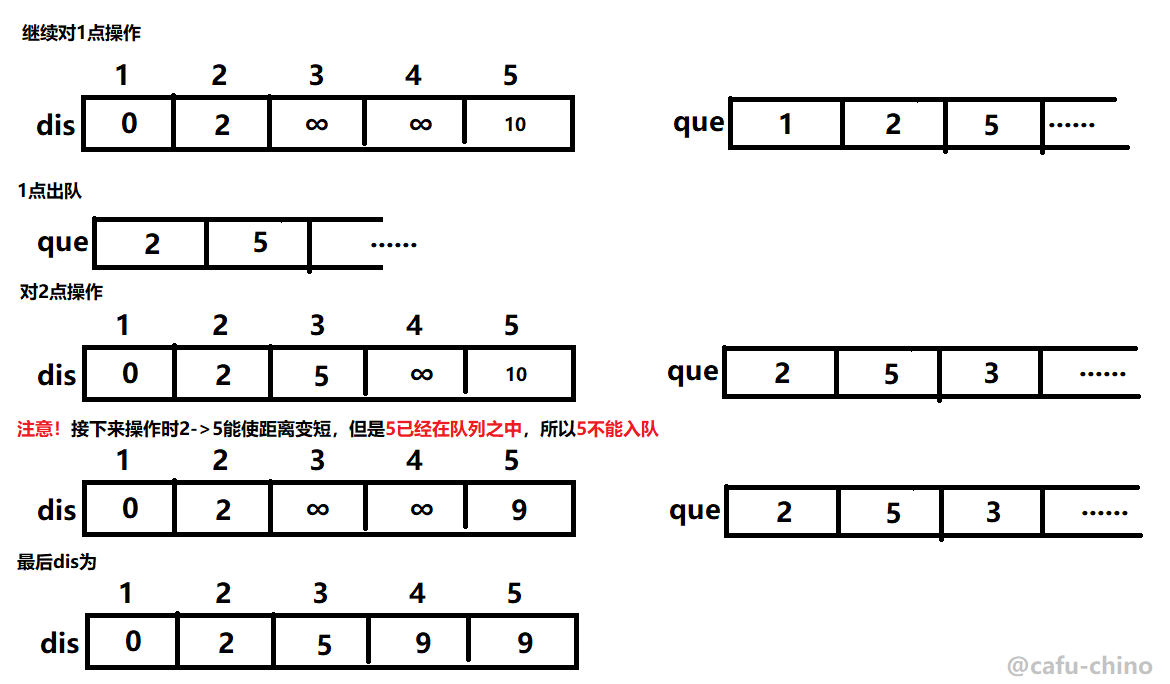
模板题
[1] POJ - 3159 Candies
Description
在幼儿园的时候,Flymouse是班上的班长。有时班主任会给班上的孩子们带来一大袋糖果,让他们分发。所有的孩子都非常喜欢糖果,经常比较他们和别人买的糖果的数量。一个孩子A可以有这样的想法,尽管可能是另一个孩子B在某些方面比他好,因此他有理由比他应得更多的糖果,但无论他实际得到多少糖果,他都不应该得到比B少的一定数量的糖果,否则他会感到不满意,去喝头茶。雪儿抱怨飞鼠的偏态分布。 当时史努比和Flymouse共享了类。Flymouse总是把他的糖果和史努比的比较,他想在让每个孩子都满意的同时,尽可能地把糖果的数量差异化。现在他又从班主任那里得到了一袋糖果,他能从中得到最大的区别是什么?
Input
输入包含单个测试用例。测试用例以两个整数n和m开始,分别不超过30000和150000。n是班上的孩子数,孩子数从1到n。snoopy和flymouse总是分别是1和n。然后按照m行,每一行依次包含三个整数a、b和c,这意味着孩子a相信孩子b永远不会比他得到更多的c糖果。
Output
只输出一行所需的最大差异。保证差异是有限的。
Sample Input
2 2
1 2 5
2 1 4
Sample Output
5
Hint
32位有符号整数类型可以执行所有算术运算。
解题思路
这道题虽然可以用SPFA去解,但是会碰到一个问题:如果正向用队列去求解的话会超时。在经历一遍又一遍的WA之后借鉴了dalao们的解法思路:用堆栈代替队列反向来求。
代码样例
#include<cstdio>
#include<cstring>
#include<stack>
#define INF 0x3f3f3f3f
using namespace std;
struct node{
int x,w,next;
}edge[150005];
bool visit[30005];
int d[30005],head[30005];
int N,M;
void spfa()
{
int i,k;
stack<int>S;
memset(visit,0,sizeof(visit));
for(i=2;i<=N;i++) d[i]=INF;
d[1]=0;
S.push(1),visit[1]=1;
while(!S.empty()){
k=S.top();
S.pop();
visit[k]=0;
for(i=head[k];i!=-1;i=edge[i].next){
if(d[edge[i].x]>edge[i].w+d[k]){
d[edge[i].x]=edge[i].w+d[k];
if(!visit[edge[i].x]){
S.push(edge[i].x);
visit[edge[i].x]=1;
}
}
}
}
printf("%d\n",d[N]);
}
int main()
{
int x,w,v,i;
while(scanf("%d%d",&N,&M)!=EOF){
memset(head,-1,sizeof(head));
for(i=1;i<=M;i++){
scanf("%d%d%d",&x,&w,&v);
edge[i].x=w;
edge[i].w=v;
edge[i].next=head[x];
head[x]=i;
}
spfa();
}
return 0;
}
全局最短路
Floyd-Warshall算法(五行代码算法)
这是最短路中关键代码最固定的算法了(仅仅只有5行);但是也是时间复杂度最高的一个复杂度$${\rm{O}}\left( {{{\rm{N}}^3}} \right)$$
空间复杂度\({\rm{O}}\left( {{{\rm{N}}^2}} \right)\),类似于动态规划(同一个人提出的)适合在稠密图中使用。
思路
即从一条边开始,不断增加中转节点(比如开始通过中间节点c,如果原本a->b的距离比a->c->b大,则更新a->b之间的距离;之后通过c,d两点,如果a->b之间的距离(即之前步骤的a->c->b的距离)比a->c->d->b大则更新a->b之间的距离。。。。。。)
核心代码
for(int k=1; k <= n; k++) //代表通过的中间节点
for(int i=1; i <= n; i++)
for(int j=1; j <= n; j++){
if(map_[i][j] > map_[i][k]+map_[k][j])
map_[i][j]=map_[i][k]+map_[k][j];
}
模板题
[1] POJ-2253 Frogger
湖中有n块石头,编号从1到n,有两只青蛙,Bob在1号石头上,Alice在2号石头上,Bob想去看望Alice,但由于水很脏,他想避免游泳,于是跳着去找她。但是Alice的石头超出了他的跳跃范围。因此,Bob使用其他石头作为中间站,通过一系列的小跳跃到达她。两块石头之间的青蛙距离被定义为两块石头之间所有可能路径上的最小必要跳跃距离,某条路径的必要跳跃距离即这条路径中单次跳跃的最远跳跃距离。你的工作是计算Alice和Bob石头之间的青蛙距离。
Input
多实例输入
先输入一个整数n表示石头数量,当n等于0时结束。
接下来2-n+1行依次给出编号为1到n的石头的坐标xi , yi。
2 <= n <= 200
0 <= xi , yi <= 1000
Output
先输出"Scenario #x", x代表样例序号。
接下来一行输出"Frog Distance = y", y代表你得到的答案。
每个样例后输出一个空行。
(ps:wa有可能是精度问题,g++不对可以用c++尝试,都不对就是代码问题)
Sample Input
2
0 0
3 4
3
17 4
19 4
18 5
0
Sample Output
Scenario #1
Frog Distance = 5.000
Scenario #2
Frog Distance = 1.414
解题思路
知道x、y点的数据,直接利用两点之间的距离公式(\(D=\sqrt{((x_1-x_2)^2+(y_1-y_2)^2}\))找到个点之间的距离之后直接套模板就OK了。
代码样例
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int maxn=1005,inf=0x3f3f3f3f;
double map_[maxn][maxn];
int x[maxn],y[maxn];
int main() {
int n,t=1;
while(cin >> n){
if(n == 0)
break;
memset(map_,0.0,sizeof(map_));
for(int i=0; i < n; i++){
map_[i][i]=0.0;
cin >> x[i] >> y[i];
for(int j=0; j < i; j++)
map_[i][j]=map_[j][i]=sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j]));
}
for(int k=0;k < n;k++)
for(int i=0;i < n;i++)
for(int j=0;j < n; j++)
if(map_[i][j]-map_[i][k]>0.0&&map_[i][j]-map_[k][j]>0.0){
if(map_[i][k]-map_[k][j] > 0.00)
map_[i][j]=map_[j][i]=map_[i][k];
else
map_[i][j]=map_[j][i]=map_[k][j];
}
printf("Scenario #%d\nFrog Distance = %.3f\n\n",t++,map_[0][1]);
}
return 0;
}
[2] POJ-3660 Cow Contest
有n(1<=n<=100)个学生参加编程比赛。
给出m条实力信息。(1<=M<=4500)
其中每一条的格式为 A B (1<=A<=N,1<=B<=N,A!=B) 意思是A的实力比B强。
如果A比B强且B比C强,那么A一定比C强。
问最后有多少名学生可以确定他的排名。
保证输入信息不存在矛盾
Input
第一行n和m。以下m行 A B 表示A实力比B强。
Output
输出答案
Sample Input
5 5
4 3
4 2
3 2
1 2
2 5
Sample Output
2
代码样例
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int maxn=110;
int dis[maxn][maxn];
int f[maxn];
int main() {
int n,m;
cin >> n >> m;
memset(dis, 0, sizeof(dis));
memset(f, 0, sizeof(f));
for (int i = 1; i <= m; i++) {
int from, to;
cin >> from >> to;
dis[from][to] = 1;
}
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
for (int k = 0; k <= n; k++)
if (dis[j][i] && dis[i][k])
dis[j][k] = 1;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
f[i] += dis[i][j];
f[j] += dis[i][j];
}
int ans = 0;
for (int i = 1; i <= n; i++)
if (f[i] == n - 1)
ans++;
cout << ans << endl;
return 0;
}
*[3] (2019南京ICPC网络赛) Holy Grail
给出一个有向图,6询问,回答由s点到t点添加的边的权值
Input
t组数据,下一行为点数n,边数m,接下来是m行为起点是x终点y的有向边、权值为w,最后6行为添加边的起止点s,t。
Output
添加边的权值每个答案各占一行
Sample Input
1
10 15
4 7 10
7 6 3
5 3 3
1 4 11
0 6 20
9 8 25
3 0 9
1 2 15
9 0 27
5 2 0
7 3 -5
1 7 21
5 0 1
9 3 16
1 8 4
4 1
0 3
6 9
2 1
8 7
0 4
Sample Output
-11
-9
-45
-15
17
7
思路
由于数据比较小所以这里采用弗洛伊德算法点之间有向的距离等于反方向取负值,但由于这里依次增加边所以要用6次弗洛伊德。这里需注意超时问题用了剪枝。也有大佬直接用6-1弗洛伊德次过了的。
代码样例
#include <bits/stdc++.h>
using namespace std;
const int inf = 1e9 + 1;
int map_[1005][1005];
int main()
{
int T;
cin >> T;
while (T--)
{
int n, m;
cin >> n >> m;
memset(map_, inf, sizeof(map_));
for (int i = 0; i < n; i++)
map_[i][i] = 0;
for (int i = 0; i < m; i++)
{
int s, t, val;
cin >> s >> t >> val;
map_[s][t] = val;
}
for (int i = 0; i < 6; i++)
{
int s, t;
cin >> s >> t;
for (int k = 0; k < n; k++)
for (int i = 0; i < n; i++) //代表通过的中间节点
for (int j = 0; j < n; j++)
{
if (i == s && j == t)
break;
else
map_[i][j] = min(map_[i][j], map_[i][k] + map_[k][j]);
}
map_[s][t] = -map_[t][s];
cout << map_[s][t] << endl;
}
}
return 0;
}
Johnson算法(稀疏图)
(因为目前用的不是太多,所以略了~)
相关注释
**松弛操作*:更新两点的最短路径; 原来有a、b两点相连,现在有一点v到b的距离更短,则把a点换成v点,使得v、b连接在一起。这样就像缓解橡皮筋紧绷的压力那样使其变得松弛,即松弛操作。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号