错排公式浅谈(推导+应用)
给出一个已经排好的长度为n的数列,问全部排错一共有多少排法?
典型利用错排公式去解决问题,
(搜一下)我们不难知道错排公式递推式为
\[D(n)=(n-1)(D(n-1)+D(n-2))
\]
特殊地,D(1) = 0, D(2) = 1.
进一步的化简即可得出
\[D(n) = n! [(-1)^2/2! + … + (-1)^{(n-1)}/(n-1)!+(-1)^n/n!]
\]
推导
首先先来解释一下递推公式(分布乘法):
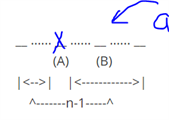
假设这组数列中有两个数a,b以及他们原来的位置(A),(B);
现在将a,b单独取出来看;
第一步错排a:去除最初存在的位置还剩下n-1个位置满足a错排的要求,即n-1
第二步排b:这里有两种情况:
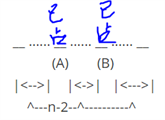
1、b在a位置上:这里只有1种剩下的n-2项再进行上述的错排,即1 * D(n-2)
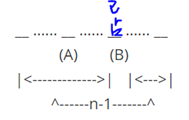
2、b不在a位置上:这里相当于n-1项再进行上述的错排,即D(n-1)
综上即可得出递推公式
\[D(n)=(n-1)(D(n-1)+D(n-2))
\]
之后进行整理:
\[D(n)=n*D(n-1)+n*D(n-2)-D(n-1)-D(n-2)
\]
递推可得
\[D(n)-n*D(n-1)=-[D(n-1)-(n-1)*D(n-2)]················1项
\]
\[D(n-1)-(n-1)D(n-2)=-[D(n-2)-(n-2)*D(n-3)]·········2项
\]
\[D(n-2)-(n-2)D(n-3)=-[D(n-3)-(n-3)*D(n-4)]·········3项
\]
\[D(n-3)-(n-3)D(n-4)=-[D(n-4)-(n-4)*D(n-5)]·········4项
\]
\[······
\]
\[D(3)-3*D(2)=-[D(2)-2*D(1)]······························n-2项
\]
同时设D(n)=n!*Nn
错项相消得
\[N(n)-N(1)=1/2!-1/3!+1/4!+······+(-1)^{(n-1)}/(n-1)!+(-1)^n/(n)!
\]
移项进一步整理(特殊的N(1)=0,N(2)=0)即可得出
\[D(n) = n! [(-1)^2/2! + … + (-1)^{(n-1)}/(n-1)!+(-1)^n/n!]
\]
应用
(懒得复制,上链接)
要计算概率=全不中奖组合数/所有组合数;
全不中奖组合数采用上面推导的错排公式即可求解
代码样例
#include <bits/stdc++.h>
using namespace std;
int main()
{
long long f[21]= {0};
f[1]=0;
f[2]=1;
for(int i=3; i<21; i++)
f[i]=(i-1)*(f[i-1]+f[i-2]);
int t,n;
cin >> t;
for(int i=0; i < t; i++)
{
cin >> n;
long long sum=1;
for(int j=2; j<=n; j++)
sum*=j;
double b=100.0*f[n]/sum;
printf("%.2f%%\n",b);
}
return 0;
}
这道题先用排列组合计算出所有m个找错新娘的新郎的组合数,之后乘以利用错排公式计算出的数据;
代码样例
#include <bits/stdc++.h>
using namespace std;
#define maxn 21
long long ci(int m,int n)
{
long long sum1=1,sum2=1;
for(int j=2; j <= m; j++)
sum1*=j;
for(int j=n; j > n-m; j--)
sum2*=j;
return sum2/sum1;
}
int main()
{
long long f[maxn]={0};
f[1]=0;
f[2]=1;
for(int i=3; i < maxn; i++)
f[i]=(i-1)*(f[i-1]+f[i-2]);
int c;
cin >> c;
for(int i=1; i <= c; i++)
{
int n,m;
cin >> n >> m;
printf("%lld\n",ci(m,n)*f[m]);
}
return 0;
}