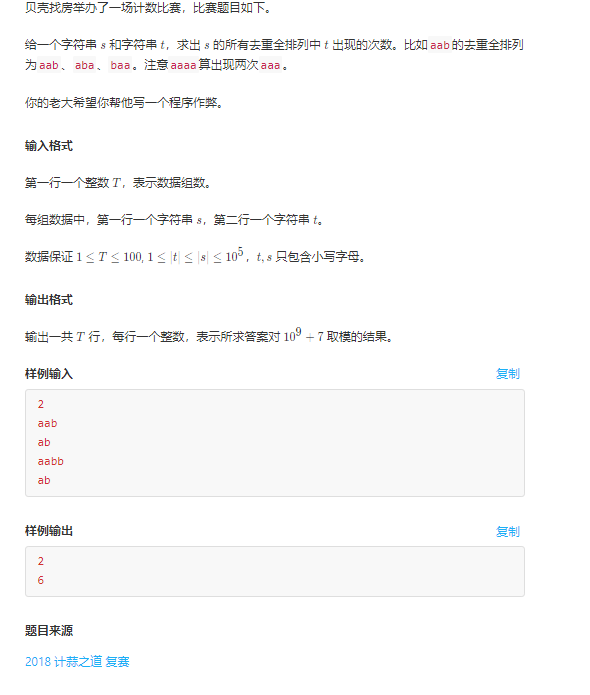
计蒜之道2018 复赛 G（排列组合）

link

思路：没注意串的大小有1e5，写了发枚举并线性匹配发现超时了。这种问题往往要逆推！题目让我们考虑str的去重全排列串中pattern的匹配次数，我们可以发现，只要str中有pattern的字母，那么，str在排列的过程中至少会出现1次的pattern。于是，根据乘法分步原理，我们优先把str中凑成pattern的字母筛掉，剩余字母进行全排列，假设剩余字母位len，那么这些字母会出现len+1个空位，利用插空法把pattern插入到这些空位中。同时，要对排列数进行去重，根据排除法依次算出每个字母的数量，分别除以这些数字的阶乘即可。

枚举+线性匹配（超时）：

#include<bits/stdc++.h>
 using namespace std;

char str[100005], res[100005], pattern[100005];
int vis[100005], prefix[100005];
int len1, len2, cnt;

void get_prefix_table (int n) {
    int i = 0, len = -1;
    prefix[0] = -1;
    while (i < n) {
        if(len == -1 || pattern[i] == pattern[len]) {
            i++;
            len++;
            prefix[i] = len;
        }else {
            len = prefix[len];
        }
    }
}

int kmp_search (int n, int m) {
    int ans = 0, i = 0, j = 0;
    while (i < n) {
        if(j == -1 || res[i] == pattern[j]) {
            i++;
            j++;
        }else {
            j = prefix[j];
        }
        if(j == m) {
            ans++;
            j = prefix[j];
        }
    }
    return ans;
}
 
void DFS(int idx) {
    if (idx == len1) {
        res[len1] = 0;
        cnt = ( cnt + kmp_search(len1, len2) ) % 1000000007;
        return ;
    }
    int i, j;
    for (i = 0; i < len1; i++) {
        if (!vis[i]) {
            for (j = i + 1; j < len1; j++) {
                if (vis[j] && str[j] == str[i])
                    break;
            }
            if (j == len1) {
                vis[i] = 1;
                res[idx] = str[i];
                DFS(idx+1);
                vis[i] = 0;
            }
        }
    }
}
 
int main() {
    int t;
    scanf("%d", &t);
    getchar();
    while (t-- && scanf("%s%s", str, pattern)) {
        getchar();
        cnt = 0;
        len1 = strlen(str);
        len2 = strlen(pattern);
        get_prefix_table (len2);        
        sort(str, str+len1);
        DFS(0);
        printf("%d\n", cnt);
    }
    return 0;
}

排列+逆元

#include <bits/stdc++.h>
using namespace std;
#define repU(i, a, b) for (int i = a; i <= b; i++)
#define repD(i, a, b) for (int i = a; i >= b; i--)
#define fast_io ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
#define LL long long
#define Ldb long double
#define Mo 1000000007
const int maxn = (int)1e5+5;

int t;
int vist[26];
char str[maxn], pattern[maxn];

LL inv(LL a) {
	LL ans = 1, b = Mo - 2;
	a %= Mo;
	while (b) {
		if (b & 1) ans = ans * a % Mo;
		a = a * a % Mo;
		b >>= 1;
	}
	return ans;
}

LL calc(LL a) {
	LL ans = 1;
	repU(i, 2, a)	ans = ans * i % Mo;
	return ans;
}

int main() {
	fast_io;
	cin >> t;
	while (t-- && cin >> str >> pattern) {
		memset(vist, 0, sizeof(vist));
		int len1 = strlen(str);
		int len2 = strlen(pattern);
		
		repU(i, 0, len1 - 1) vist[str[i] - 'a']++;
		bool flag = false;
		repU(i, 0, len2 - 1) {
			if (vist[pattern[i] - 'a'] == 0) { //发现pattern的某个字母未出现
				cout << 0 << endl;
				flag = true;
				break;
			}
			vist[pattern[i] - 'a']--;
		}
		if (flag) continue;
		
		len1 -= len2; //扣除掉pattern的剩余字母进行去重全排列，最后把pattern通过插空的策略还原
		LL ans = 1;
		repU(i, 0, 25) {
			ans = ans * calc(vist[i]) % Mo;
		}
		cout << ( ( calc(len1) * inv(ans) ) % Mo ) * (len1 + 1) % Mo << endl;
	}
	return 0;
}