Luogu P4059 找爸爸
找爸爸
题目描述
小A最近一直在找自己的爸爸，用什么办法呢，就是DNA比对。
小A有一套自己的DNA序列比较方法，其最终目标是最大化两个DNA序列的相似程度，具体步骤如下：
-
给出两个DNA序列，第一个长度为\(n\)，第二个长度为\(m\)。
-
在两个序列的任意位置插入任意多的空格，使得两个字符串长度相同
-
逐位进行匹配，如果两个序列相同位置上的字符都不是空格，假设第一个是\(x\)，第二个是\(y\)，那么他们的相似程度由\(d(x,y)\)定义。对于两个序列中任意一段极长的长度为\(k\)的连续空格，我们定义这段空格的相似程度为\(g(k)=-A-B(k-1)\)。
那么最终两个序列的相似程度就是所有的\(d(x,y)\)加上所有的极长空格段的相似程度之和。
现在小A通过某种奥妙重重的方式得到了小B的DNA序列中的一段，他想请你帮他算一下小A的DNA序列和小B的DNA序列的最大相似程度。
输入格式
输入第\(1\)行一个字符串，表示小A的DNA序列。
输入第\(2\)行一个字符串，表示小B的DNA序列。
接下来\(4\)行，每行\(4\)个整数，用空格隔开，表示\(d\)数组，具体顺序如下所示。
d(A,A) d(A,T) d(A,G) d(A,C)
d(T,A) d(T,T) d(T,G) d(T,C)
d(G,A) d(G,T) d(G,G) d(G,C)
d(C,A) d(C,T) d(C,G) d(C,C)
最后一行两个用空格隔开的正整数\(A,B\)，意义如题中所述。
输出格式
输出共一行，表示两个序列的最大相似程度。
样例 #1
样例输入 #1
ATGG
ATCC
5 -4 -4 -4
-4 5 -4 -4
-4 -4 5 -4
-4 -4 -4 5
2 1
样例输出 #1
4
提示
样例解释
首先，将序列补成如下形式（"-"代表空格）
ATGG--
AT--CC
然后所有\(d(x,y)\)的和为\(d(A,A)+d(T,T)=10\)
所有极长连续空格段的相似程度之和为\(g(2)+g(2)=-6\)
总和为\(4\)，可以验证，这是相似程度最大的情况。
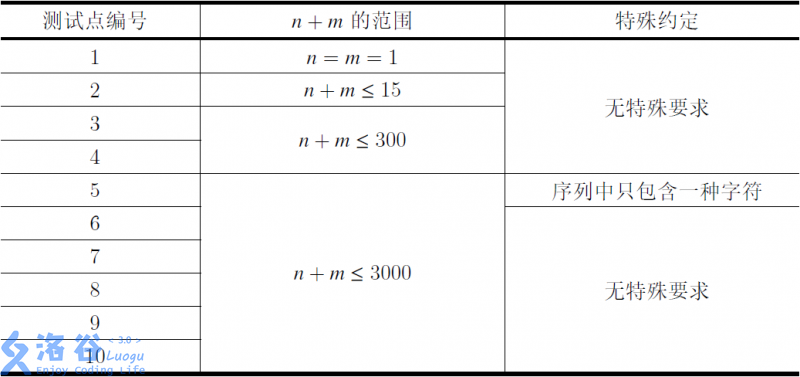
对于所有测试点，有\(0< B<A \le 1000, -1000\le d(x,y)\le 1000,d(x,y)=d(y,x)\)，序列只包含\({A,T,G,C}\)四种字符。
SOLUTION
首先我们考虑每个位置上的字符：
- 如果两个都为字符，那么它的贡献是给定的一个值
- 如果一个是空格一个是字符，那么他的贡献需要考虑他是的前一个是否也是空格
- 如果是第一个空格，则贡献为 \(-a\)
- 如果不是第一个空格，则贡献为 \(-b\)
- 如果连个都为空格，那么他的贡献不会增加，因此我们舍弃这种情况。
因此我们对于某个位置，只需要记录它的前一个位置的情况即可。
可以定义 \(f[i][j][0/1/2]\) 分别表示 \(A\) 使用了 \(i\) 个字符 \(B\) 使用了 \(j\) 个字符 并且最后一对字符为：
- 0 均为字符
- 1 \(A\)为空格，\(B\)为字符
- 2 \(B\)为空格，\(A\)为字符
然后进行状态转移即可
CODE
#include <bits/stdc++.h>
using namespace std;
#define rep(i, b, s) for(int i = (b); i <= (s); ++ i)
#define dec(i, b, s) for(int i = (b); i >= (s); -- i)
#define YES cout << "YES" << "\n"; return
#define NO cout << "NO" << "\n"; return
using ll = long long;
#ifdef LOCAL
#include <debugger>
#else
#define debug(...) 42
#endif
template <typename T> void chkmax(T &x, T y) { x = max(x, y); }
template <typename T> void chkmin(T &x, T y) { x = min(x, y); }
constexpr ll inf = 1e18;
map<pair<char, char>, int> mp;
void solve() {
string s1, s2; cin >> s1 >> s2;
int n = s1.size(), m = s2.size();
s1 = " " + s1;
s2 = " " + s2;
vector<char> all{'A', 'T', 'G', 'C'};
for(int i = 0; i < 4; i ++ ) {
for(int j = 0; j < 4; j ++ ) {
int x; cin >> x;
mp[{all[i], all[j]}] = x;
}
}
// cout << mp[{'G', 'C'}] << "\n";
ll x, y; cin >> x >> y;
vector<vector<array<ll, 3> > > f(n + 1, vector<array<ll, 3> >(m + 1, {-inf, -inf, -inf}));
for(int i = 1; i <= n || i <= m; ++ i ) {
if(i <= m) {
f[0][i][1] = -x - y * (i - 1);
}
if(i <= n) {
f[i][0][2] = -x - y * (i - 1);
}
}
f[0][0][0] = 0;
//f[i][j][0] 表示s1匹配了i个， s2匹配了j个，并且当前状态为两个字符
//f[i][j][1] 表示s1匹配了i个， s2匹配了j个，并且当前状态为s1是空格，s2是字符
//f[i][j][2] 表示s1匹配了i个， s2匹配了j个，并且当前状态为s1是字符，s2是空格
for (int i = 1; i <= n; i ++ ) {
for (int j = 1; j <= m; j ++ ) {
//
//
f[i][j][0] = max({f[i - 1][j - 1][0], f[i - 1][j - 1][1], f[i - 1][j - 1][2]}) + mp[{s1[i], s2[j]}];
f[i][j][1] = max({f[i][j - 1][0] - x, f[i][j - 1][1] - y, f[i][j - 1][2] - x});
f[i][j][2] = max({f[i - 1][j][0] - x, f[i - 1][j][1] - x, f[i - 1][j][2] - y});
// f[i][j][1] = max({f[i - 1][j][0], f[i - 1][j][2]});
// f[i][j][2] = max({f[i][j - 1][0], f[i][j - 1][1]});
// printf("%d %d -> %lld %lld %lld\n", i, j, f[i][j][0], f[i][j][1], f[i][j][2]);
// printf("f[%d][%d][%d] = %lld\n", i, j, )
}
}
// cout << f[1][1][1] << "\n";
cout << max({f[n][m][0], f[n][m][1], f[n][m][2]}) << "\n";
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T = 1; //cin >> T;
while(T -- ) solve();
return 0;
}
