斐波那契数列-递归优化

斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家莱昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：0、1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列被以递推的方法定义：F(1)=1, F(2)=1, F(n)=F(n - 2)+F(n - 1)

递归实现

function fib(n) {
  if (n === 1 || n === 2) return 1
  return fib(n-1) + fib(n-2)
}

递归的缺点：
在递归执行的时候，会调用一个又一个的函数，每次调用函数的时候都会压入调用栈，直到得到一个返回值，才会一级一级的出栈，比如：同事A让同事B帮忙解决一个问题，B又找同事C帮忙，如果C能够解决问题告诉B，B得到答案（出栈），B再告诉A，A得到答案（出栈），未解决问题之前，A和B都压入了调用栈，如果调用的函数太多，而栈的内存有限，就会出现栈溢出

递归的另一个缺点就是重复计算，插入代码console.log(`fib2(${n-1}) + fib2(${n-2})`)运行fib(5)

"fib2(4) + fib2(3)"
"fib2(3) + fib2(2)"
"fib2(2) + fib2(1)"
"fib2(2) + fib2(1)"

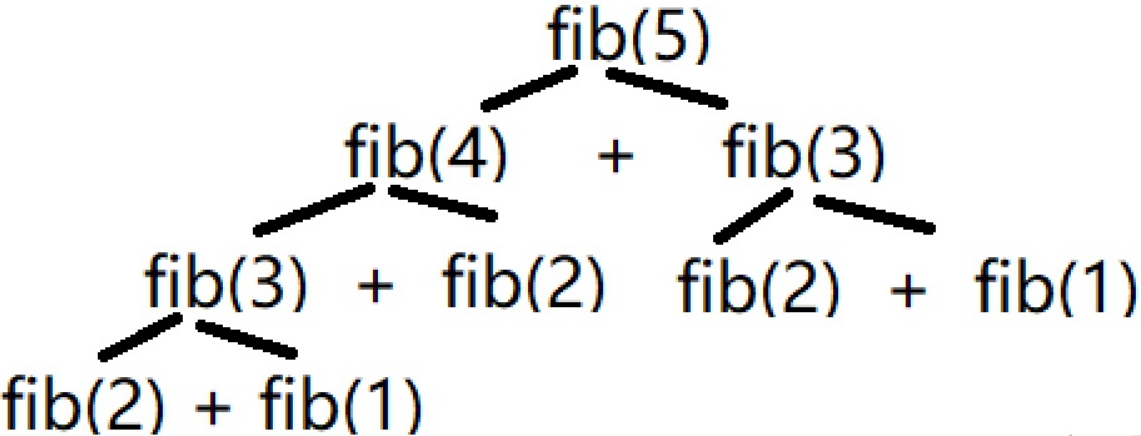
递归优化

1. 非递归实现

function fn(n) {
  let last1 = 1, last2 = 1, temp
  for(let i = 3; i <=n; i++) {
    temp = last1 + last2
    last1 = last2
    last2 = temp
  }
  return last2
}

2. 用空间换效率

function fib(n) {
  let arr = [0, 1, 1]
  for(let i=3; i<=n; i++) {
    arr[i] = arr[i-1] + arr[i-2]
  }
  return arr[n]
}

3. 使用缓存提升效率
   定义一个缓存数组，存储已经计算过的数列，每次计算前看看数组里有没有，如果有直接用，如果没有就计算，然后存在数组，以便下一次计算使用

function fib(n) {
  let cache = [0, 1, 1]
  function _fib(n) {
    if(cache[n]) return cache[n]
    cache[n] = _fib(n-1) + _fib(n-2)
    return cache[n]
  }
  return _fib(n)
}