A*算法详解 BZOJ 1085骑士精神

转载1：A*算法入门

http://www.cppblog.com/mythit/archive/2009/04/19/80492.aspx

在看下面这篇文章之前，先介绍几个理论知识，有助于理解A*算法。

 

启发式搜索：启发式搜索就是在状态空间中的搜索对每一个搜索的位置进行评估，得到最好的位置，再从这个位置进行搜索直到目标。这样可以省略大量无畏的搜索路径，提到了效率。在启发式搜索中，对位置的估价是十分重要的。采用了不同的估价可以有不同的效果。

估价函数：从当前节点移动到目标节点的预估费用；这个估计就是启发式的。在寻路问题和迷宫问题中，我们通常用曼哈顿（manhattan）估价函数（下文有介绍）预估费用。

A*算法与BFS：可以这样说，BFS是A*算法的一个特例。对于一个BFS算法，从当前节点扩展出来的每一个节点（如果没有被访问过的话）都要放进队列进行进一步扩展。也就是说BFS的估计函数h永远等于0，没有一点启发式的信息，可以认为BFS是“最烂的”A*算法。

选取最小估价：如果学过数据结构的话，应该可以知道，对于每次都要选取最小估价的节点，应该用到最小优先级队列（也叫最小二叉堆）。在C++的STL里有现成的数据结构priority_queue，可以直接使用。当然不要忘了重载自定义节点的比较操作符。

A*算法的特点：A*算法在理论上是时间最优的，但是也有缺点：它的空间增长是指数级别的。

IDA*算法：这种算法被称为迭代加深A*算法，可以有效的解决A*空间增长带来的问题，甚至可以不用到优先级队列。如果要知道详细：google一下。

 

A*寻路初探（转载）

 

作者：Patrick Lester

译者：Panic2005年

 

译者序：很久以前就知道了A*算法，但是从未认真读过相关的文章，也没有看过代码，只是脑子里有个模糊的概念。这次决定从头开始，研究一下这个被人推崇备至的简单方法，作为学习人工智能的开始。

这篇文章非常知名，国内应该有不少人翻译过它，我没有查找，觉得翻译本身也是对自身英文水平的锻炼。经过努力，终于完成了文档，也明白的A*算法的原理。毫无疑问，作者用形象的描述，简洁诙谐的语言由浅入深的讲述了这一神奇的算法，相信每个读过的人都会对此有所认识（如果没有，那就是偶的翻译太差了--b）。

现在是年月日的版本，应原作者要求，对文中的某些算法细节做了修改。

原文链接：http://www.gamedev.net/reference/articles/article2003.asp

原作者文章链接：http://www.policyalmanac.org/games/aStarTutorial.htm

以下是翻译的正文

会者不难，A*(念作A星)算法对初学者来说的确有些难度。这篇文章并不试图对这个话题作权威的陈述。取而代之的是，它只是描述算法的原理，使你可以在进一步的阅读中理解其他相关的资料。最后，这篇文章没有程序细节。你尽可以用任意的计算机程序语言实现它。如你所愿，我在文章的末尾包含了一个指向例子程序的链接。压缩包包括C++和Blitz Basic两个语言的版本，如果你只是想看看它的运行效果，里面还包含了可执行文件。我们正在提高自己。让我们从头开始。。。

 

序：搜索区域

假设有人想从A点移动到一墙之隔的B点，如下图，绿色的是起点A，红色是终点B，蓝色方块是中间的墙。

[图-1]

你首先注意到，搜索区域被我们划分成了方形网格。像这样，简化搜索区域，是寻路的第一步。这一方法把搜索区域简化成了一个二维数组。数组的每一个元素是网格的一个方块，方块被标记为可通过的和不可通过的。路径被描述为从A到B我们经过的方块的集合。一旦路径被找到，我们的人就从一个方格的中心走向另一个，直到到达目的地。

这些中点被称为“节点”。当你阅读其他的寻路资料时，你将经常会看到人们讨论节点。为什么不把他们描述为方格呢？因为有可能你的路径被分割成其他不是方格的结构。他们完全可以是矩形，六角形，或者其他任意形状。节点能够被放置在形状的任意位置－可以在中心，或者沿着边界，或其他什么地方。我们使用这种系统，无论如何，因为它是最简单的。

开始搜索

正如我们处理上图网格的方法，一旦搜索区域被转化为容易处理的节点，下一步就是去引导一次找到最短路径的搜索。在A*寻路算法中，我们通过从点A开始，检查相邻方格的方式，向外扩展直到找到目标。

我们做如下操作开始搜索：

 

   1，从点A开始，并且把它作为待处理点存入一个“开启列表”。开启列表就像一张购物清单。尽管现在列表里只有一个元素，但以后就会多起来。你的路径可能会通过它包含的方格，也可能不会。基本上，这是一个待检查方格的列表。

   2，寻找起点周围所有可到达或者可通过的方格，跳过有墙，水，或其他无法通过地形的方格。也把他们加入开启列表。为所有这些方格保存点A作为“父方格”。当我们想描述路径的时候，父方格的资料是十分重要的。后面会解释它的具体用途。

   3，从开启列表中删除点A，把它加入到一个“关闭列表”，列表中保存所有不需要再次检查的方格。在这一点，你应该形成如图的结构。在图中，暗绿色方格是你起始方格的中心。它被用浅蓝色描边，以表示它被加入到关闭列表中了。所有的相邻格现在都在开启列表中，它们被用浅绿色描边。每个方格都有一个灰色指针反指他们的父方格，也就是开始的方格。

[图-2]

接着，我们选择开启列表中的临近方格，大致重复前面的过程，如下。但是，哪个方格是我们要选择的呢？是那个F值最低的。

路径评分

选择路径中经过哪个方格的关键是下面这个等式：F = G + H

这里：

    * G = 从起点A，沿着产生的路径，移动到网格上指定方格的移动耗费。

    * H = 从网格上那个方格移动到终点B的预估移动耗费。这经常被称为启发式的，可能会让你有点迷惑。这样叫的原因是因为它只是个猜测。我们没办法事先知道路径的长度，因为路上可能存在各种障碍(墙，水，等等)。虽然本文只提供了一种计算H的方法，但是你可以在网上找到很多其他的方法。

我们的路径是通过反复遍历开启列表并且选择具有最低F值的方格来生成的。文章将对这个过程做更详细的描述。首先，我们更深入的看看如何计算这个方程。

正如上面所说，G表示沿路径从起点到当前点的移动耗费。在这个例子里，我们令水平或者垂直移动的耗费为，对角线方向耗费为。我们取这些值是因为沿对角线的距离是沿水平或垂直移动耗费的的根号（别怕），或者约.414倍。为了简化，我们用和近似。比例基本正确，同时我们避免了求根运算和小数。这不是只因为我们怕麻烦或者不喜欢数学。使用这样的整数对计算机来说也更快捷。你不就就会发现，如果你不使用这些简化方法，寻路会变得很慢。

既然我们在计算沿特定路径通往某个方格的G值，求值的方法就是取它父节点的G值，然后依照它相对父节点是对角线方向或者直角方向(非对角线)，分别增加和。例子中这个方法的需求会变得更多，因为我们从起点方格以外获取了不止一个方格。

H值可以用不同的方法估算。我们这里使用的方法被称为曼哈顿方法，它计算从当前格到目的格之间水平和垂直的方格的数量总和，忽略对角线方向，然后把结果乘以10。这被称为曼哈顿方法是因为它看起来像计算城市中从一个地方到另外一个地方的街区数，在那里你不能沿对角线方向穿过街区。很重要的一点，我们忽略了一切障碍物。这是对剩余距离的一个估算，而非实际值，这也是这一方法被称为启发式的原因。想知道更多？你可以在这里找到方程和额外的注解。

F的值是G和H的和。第一步搜索的结果可以在下面的图表中看到。F,G和H的评分被写在每个方格里。正如在紧挨起始格右侧的方格所表示的，F被打印在左上角，G在左下角，H则在右下角。

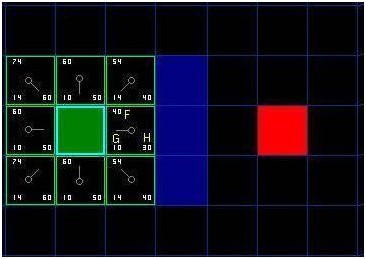
[图-3]

现在我们来看看这些方格。写字母的方格里，G = 10。这是因为它只在水平方向偏离起始格一个格距。紧邻起始格的上方，下方和左边的方格的G值都等于。对角线方向的G值是。

H值通过求解到红色目标格的曼哈顿距离得到，其中只在水平和垂直方向移动，并且忽略中间的墙。用这种方法，起点右侧紧邻的方格离红色方格有格距离，H值就是。这块方格上方的方格有格距离(记住，只能在水平和垂直方向移动)，H值是。你大致应该知道如何计算其他方格的H值了～。每个格子的F值，还是简单的由G和H相加得到

继续搜索

为了继续搜索，我们简单的从开启列表中选择F值最低的方格。然后，对选中的方格做如下处理：

   4，把它从开启列表中删除，然后添加到关闭列表中。

   5，检查所有相邻格子。跳过那些已经在关闭列表中的或者不可通过的(有墙，水的地形，或者其他无法通过的地形)，把他们添加进开启列表，如果他们还不在里面的话。把选中的方格作为新的方格的父节点。

   6，如果某个相邻格已经在开启列表里了，检查现在的这条路径是否更好。换句话说，检查如果我们用新的路径到达它的话，G值是否会更低一些。如果不是，那就什么都不做。

      另一方面，如果新的G值更低，那就把相邻方格的父节点改为目前选中的方格（在上面的图表中，把箭头的方向改为指向这个方格）。最后，重新计算F和G的值。如果这看起来不够清晰，你可以看下面的图示。

好了，让我们看看它是怎么运作的。我们最初的格方格中，在起点被切换到关闭列表中后，还剩格留在开启列表中。这里面，F值最低的那个是起始格右侧紧邻的格子，它的F值是。因此我们选择这一格作为下一个要处理的方格。在紧随的图中，它被用蓝色突出显示。

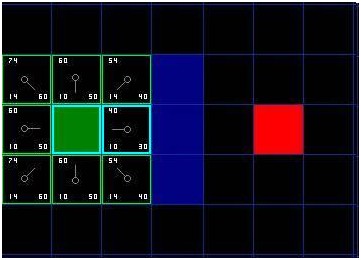
[图-4]

首先，我们把它从开启列表中取出，放入关闭列表(这就是他被蓝色突出显示的原因)。然后我们检查相邻的格子。哦，右侧的格子是墙，所以我们略过。左侧的格子是起始格。它在关闭列表里，所以我们也跳过它。

其他格已经在开启列表里了，于是我们检查G值来判定，如果通过这一格到达那里，路径是否更好。我们来看选中格子下面的方格。它的G值是。如果我们从当前格移动到那里，G值就会等于(到达当前格的G值是，移动到上面的格子将使得G值增加)。因为G值大于，所以这不是更好的路径。如果你看图，就能理解。与其通过先水平移动一格，再垂直移动一格，还不如直接沿对角线方向移动一格来得简单。

当我们对已经存在于开启列表中的个临近格重复这一过程的时候，我们发现没有一条路径可以通过使用当前格子得到改善，所以我们不做任何改变。既然我们已经检查过了所有邻近格，那么就可以移动到下一格了。

于是我们检索开启列表，现在里面只有7格了，我们仍然选择其中F值最低的。有趣的是，这次，有两个格子的数值都是。我们如何选择？这并不麻烦。从速度上考虑，选择最后添加进列表的格子会更快捷。这种导致了寻路过程中，在靠近目标的时候，优先使用新找到的格子的偏好。但这无关紧要。（对相同数值的不同对待，导致不同版本的A*算法找到等长的不同路径）那我们就选择起始格右下方的格子，如图：

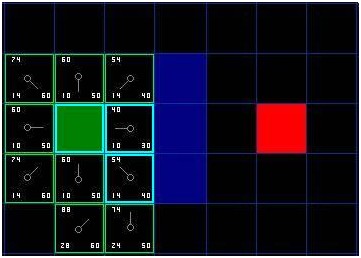
[图-5]

这次，当我们检查相邻格的时候，发现右侧是墙，于是略过。上面一格也被略过。我们也略过了墙下面的格子。为什么呢？因为你不能在不穿越墙角的情况下直接到达那个格子。你的确需要先往下走然后到达那一格，按部就班的走过那个拐角。(注解：穿越拐角的规则是可选的。它取决于你的节点是如何放置的。)

这样一来，就剩下了其他格。当前格下面的另外两个格子目前不在开启列表中，于是我们添加他们，并且把当前格指定为他们的父节点。其余格，两个已经在关闭列表中（起始格，和当前格上方的格子，在表格中蓝色高亮显示),于是我们略过它们。最后一格，在当前格的左侧，将被检查通过这条路径，G值是否更低。不必担心，我们已经准备好检查开启列表中的下一格了。

我们重复这个过程，直到目标格被添加进关闭列表(注解)，就如在下面的图中所看到的。

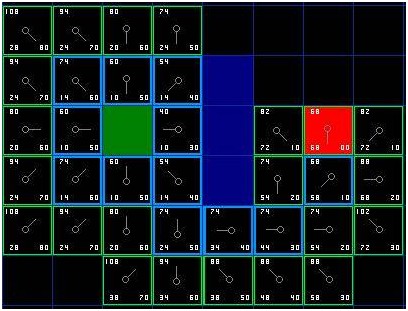
[图-6]

注意，起始格下方格子的父节点已经和前面不同的。之前它的G值是，并且指向右上方的格子。现在它的G值是，指向它上方的格子。这在寻路过程中的某处发生，当应用新路径时，G值经过检查变得低了－于是父节点被重新指定，G和F值被重新计算。尽管这一变化在这个例子中并不重要，在很多场合，这种变化会导致寻路结果的巨大变化。

那么，我们怎么确定这条路径呢？很简单，从红色的目标格开始，按箭头的方向朝父节点移动。这最终会引导你回到起始格，这就是你的路径！看起来应该像图中那样。从起始格A移动到目标格B只是简单的从每个格子（节点）的中点沿路径移动到下一个，直到你到达目标点。就这么简单。

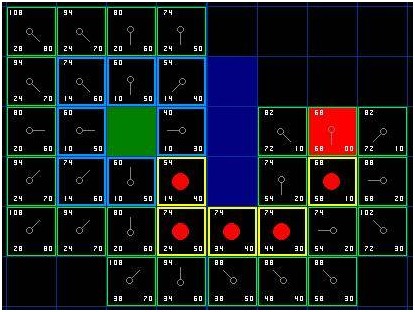
[图-7]

A*方法总结

好，现在你已经看完了整个说明，让我们把每一步的操作写在一起：

   1，把起始格添加到开启列表。

   2，重复如下的工作：

      a) 寻找开启列表中F值最低的格子。我们称它为当前格。

      b) 把它切换到关闭列表。

      c) 对相邻的格中的每一个？

          * 如果它不可通过或者已经在关闭列表中，略过它。反之如下。

          * 如果它不在开启列表中，把它添加进去。把当前格作为这一格的父节点。记录这一格的F,G,和H值。

          * 如果它已经在开启列表中，用G值为参考检查新的路径是否更好。更低的G值意味着更好的路径。如果是这样，就把这一格的父节点改成当前格，并且重新计算这一格的G和F值。如果你保持你的开启列表按F值排序，改变之后你可能需要重新对开启列表排序。

      d) 停止，当你

          * 把目标格添加进了关闭列表(注解)，这时候路径被找到，或者

          * 没有找到目标格，开启列表已经空了。这时候，路径不存在。

   3.保存路径。从目标格开始，沿着每一格的父节点移动直到回到起始格。这就是你的路径。

 

(注解:在这篇文章的较早版本中，建议的做法是当目标格（或节点）被加入到开启列表，而不是关闭列表的时候停止寻路。这么做会更迅速，而且几乎总是能找到最短的路径，但不是绝对的。当从倒数第二个节点到最后一个（目标节点）之间的移动耗费悬殊很大时－例如刚好有一条河穿越两个节点中间，这时候旧的做法和新的做法就会有显著不同。)

 

题外话

离题一下，见谅，值得一提的是，当你在网上或者相关论坛看到关于A*的不同的探讨，你有时会看到一些被当作A*算法的代码而实际上他们不是。要使用A*，你必须包含上面讨论的所有元素－－特定的开启和关闭列表，用F,G和H作路径评价。有很多其他的寻路算法，但他们并不是A*，A*被认为是他们当中最好的。Bryan Stout在这篇文章后面的参考文档中论述了一部分，包括他们的一些优点和缺点。有时候特定的场合其他算法会更好，但你必须很明确你在作什么。好了，够多的了。回到文章。

 

实现的注解

现在你已经明白了基本原理，写你的程序的时候还得考虑一些额外的东西。下面这些材料中的一些引用了我用C++和Blitz Basic写的程序，但对其他语言写的代码同样有效。

1.其他单位(避免碰撞)：如果你恰好看了我的例子代码，你会发现它完全忽略了其他单位。我的寻路者事实上可以相互穿越。取决于具体的游戏，这也许可以，也许不行。如果你打算考虑其他单位，希望他们能互相绕过，我建议你只考虑静止或那些在计算路径时临近当前单位的单位，把它们当前的位置标志为可通过的。对于临近的运动着的单位，你可以通过惩罚它们各自路径上的节点，来鼓励这些寻路者找到不同的路径(更多的描述见#2).

如果你选择了把其他正在移动并且远离当前寻路单位的那些单位考虑在内，你将需要实现一种方法及时预测在何时何地碰撞可能会发生，以便恰当的避免。否则你极有可能得到一条怪异的路径，单位突然转弯试图避免和一个已经不存在的单位发生碰撞。

当然，你也需要写一些碰撞检测的代码，因为无论计算的时候路径有多完美，它也会因时间而改变。当碰撞发生时，一个单位必须寻找一条新路径，或者，如果另一个单位正在移动并且不是正面碰撞，在继续沿当前路径移动之前，等待那个单位离开。

这些提示大概可以让你开始了。如果你想了解更多，这里有些你可能会觉得有用的链接：

    *自治角色的指导行为：Craig Reynold在指导能力上的工作和寻路有些不同，但是它可以和寻路整合从而形成更完整的移动和碰撞检测系统。

    *电脑游戏中的长短距指导：指导和寻路方面著作的一个有趣的考察。这是一个pdf文件。

    *协同单位移动：一个两部分系列文章的第一篇，内容是关于编队和基于分组的移动，作者是帝国时代(Age of Empires)的设计者Dave Pottinger.

    *实现协同移动：Dave Pottinger文章系列的第二篇。

2. 不同的地形损耗：在这个教程和我附带的程序中，地形只能是二者之－可通过的和不可通过的。但是你可能会需要一些可通过的地形，但是移动耗费更高－沼泽，小山，地牢的楼梯，等等。这些都是可通过但是比平坦的开阔地移动耗费更高的地形。类似的，道路应该比自然地形移动耗费更低。

这个问题很容易解决，只要在计算任何地形的G值的时候增加地形损耗就可以了。简单的给它增加一些额外的损耗就可以了。由于A*算法已经按照寻找最低耗费的路径来设计，所以很容易处理这种情况。在我提供的这个简单的例子里，地形只有可通过和不可通过两种，A*会找到最短，最直接的路径。但是在地形耗费不同的场合，耗费最低的路径也许会包含很长的移动距离－就像沿着路绕过沼泽而不是直接穿过它。

一种需额外考虑的情况是被专家称之为“influence mapping”的东西（暂译为影响映射图）。就像上面描述的不同地形耗费一样，你可以创建一格额外的分数系统，并把它应用到寻路的AI中。假设你有一张有大批寻路者的地图，他们都要通过某个山区。每次电脑生成一条通过那个关口的路径，它就会变得更拥挤。如果你愿意，你可以创建一个影响映射图对有大量屠杀事件的格子施以不利影响。这会让计算机更倾向安全些的路径，并且帮助它避免总是仅仅因为路径短(但可能更危险)而持续把队伍和寻路者送到某一特定路径。

另一个可能得应用是惩罚周围移动单位路径上得节点。A*的一个底限是，当一群单位同时试图寻路到接近的地点，这通常会导致路径交叠。以为一个或者多个单位都试图走相同或者近似的路径到达目的地。对其他单位已经“认领”了的节点增加一些惩罚会有助于你在一定程度上分离路径，降低碰撞的可能性。然而，如果有必要，不要把那些节点看成不可通过的，因为你仍然希望多个单位能够一字纵队通过拥挤的出口。同时，你只能惩罚那些临近单位的路径，而不是所有路径，否则你就会得到奇怪的躲避行为例如单位躲避路径上其他已经不在那里的单位。还有，你应该只惩罚路径当前节点和随后的节点，而不应处理已经走过并甩在身后的节点。

3. 处理未知区域：你是否玩过这样的PC游戏，电脑总是知道哪条路是正确的，即使它还没有侦察过地图？对于游戏，寻路太好会显得不真实。幸运的是，这是一格可以轻易解决的问题。

答案就是为每个不同的玩家和电脑（每个玩家，而不是每个单位－－那样的话会耗费大量的内存）创建一个独立的“knownWalkability”数组，每个数组包含玩家已经探索过的区域，以及被当作可通过区域的其他区域，直到被证实。用这种方法，单位会在路的死端徘徊并且导致错误的选择直到他们在周围找到路。一旦地图被探索了，寻路就像往常那样进行。

4. 平滑路径：尽管A*提供了最短，最低代价的路径，它无法自动提供看起来平滑的路径。看一下我们的例子最终形成的路径（在图）。最初的一步是起始格的右下方，如果这一步是直接往下的话，路径不是会更平滑一些吗？有几种方法来解决这个问题。当计算路径的时候可以对改变方向的格子施加不利影响，对G值增加额外的数值。也可以换种方法，你可以在路径计算完之后沿着它跑一遍，找那些用相邻格替换会让路径看起来更平滑的地方。想知道完整的结果，查看Toward More Realistic Pathfinding，一篇(免费，但是需要注册)Marco Pinter发表在Gamasutra.com的文章

5. 非方形搜索区域：在我们的例子里，我们使用简单的D方形图。你可以不使用这种方式。你可以使用不规则形状的区域。想想冒险棋的游戏，和游戏中那些国家。你可以设计一个像那样的寻路关卡。为此，你可能需要建立一个国家相邻关系的表格，和从一个国家移动到另一个的G值。你也需要估算H值的方法。其他的事情就和例子中完全一样了。当你需要向开启列表中添加新元素的时候，不需使用相邻的格子，取而代之的是从表格中寻找相邻的国家。

类似的，你可以为一张确定的地形图创建路径点系统，路径点一般是路上，或者地牢通道的转折点。作为游戏设计者，你可以预设这些路径点。两个路径点被认为是相邻的如果他们之间的直线上没有障碍的话。在冒险棋的例子里，你可以保存这些相邻信息在某个表格里，当需要在开启列表中添加元素的时候使用它。然后你就可以记录关联的G值（可能使用两点间的直线距离），H值（可以使用到目标点的直线距离），其他都按原先的做就可以了。Amit Patel 写了其他方法的摘要。另一个在非方形区域搜索RPG地图的例子，查看我的文章Two-Tiered A* Pathfinding。(译者注：译文： A*分层寻路)

6. 一些速度方面的提示：当你开发你自己的A*程序，或者改写我的，你会发现寻路占据了大量的CPU时间，尤其是在大地图上有大量对象在寻路的时候。如果你阅读过网上的其他材料，你会明白，即使是开发了星际争霸或帝国时代的专家，这也无可奈何。如果你觉得寻路太过缓慢，这里有一些建议也许有效：

    * 使用更小的地图或者更少的寻路者。

    * 不要同时给多个对象寻路。取而代之的是把他们加入一个队列，把寻路过程分散在几个游戏周期中。如果你的游戏以周期每秒的速度运行，没人能察觉。但是当大量寻路者计算自己路径的时候,他们会发觉游戏速度突然变慢。

    * 尽量使用更大的地图网格。这降低了寻路中搜索的总网格数。如果你有志气，你可以设计两个或者更多寻路系统以便使用在不同场合，取决于路径的长度。这也正是专业人士的做法，用大的区域计算长的路径，然后在接近目标的时候切换到使用小格子/区域的精细寻路。如果你对这个观点感兴趣，查阅我的文章Two-Tiered A* Pathfinding。(译者注：译文:A*分层寻路)

    * 使用路径点系统计算长路径，或者预先计算好路径并加入到游戏中。

    * 预处理你的地图，表明地图中哪些区域是不可到达的。我把这些区域称作“孤岛”。事实上，他们可以是岛屿或其他被墙壁包围等无法到达的任意区域。A*的下限是，当你告诉它要寻找通往那些区域的路径时，它会搜索整个地图，直到所有可到达的方格/节点都被通过开启列表和关闭列表的计算。这会浪费大量的CPU时间。可以通过预先确定这些区域（比如通过flood-fill或类似的方法)来避免这种情况的发生,用某些种类的数组记录这些信息，在开始寻路前检查它。

    * 在一个拥挤的类似迷宫的场合，把不能连通的节点看作死端。这些区域可以在地图编辑器中预先手动指定，或者如果你有雄心壮志，开发一个自动识别这些区域的算法。给定死端的所有节点可以被赋予一个唯一的标志数字。然后你就可以在寻路过程中安全的忽略所有死端，只有当起点或者终点恰好在死端的某个节点的时候才需要考虑它们。

7. 维护开启列表：这是A*寻路算法最重要的组成部分。每次你访问开启列表，你都需要寻找F值最低的方格。有几种不同的方法实现这一点。你可以把路径元素随意保存，当需要寻找F值最低的元素的时候，遍历开启列表。这很简单，但是太慢了，尤其是对长路径来说。这可以通过维护一格排好序的列表来改善，每次寻找F值最低的方格只需要选取列表的首元素。当我自己实现的时候，这种方法是我的首选。

在小地图。这种方法工作的很好，但它并不是最快的解决方案。更苛求速度的A*程序员使用叫做二叉堆的方法，这也是我在代码中使用的方法。凭我的经验，这种方法在大多数场合会快～倍，并且在长路经上速度呈几何级数提升(10倍以上速度)。如果你想了解更多关于二叉堆的内容，查阅我的文章，Using Binary Heaps in A* Pathfinding。(译者注：译文：在A*寻路中使用二叉堆)

另一个可能的瓶颈是你在多次寻路之间清除和保存你的数据结构的方法。我个人更倾向把所有东西都存储在数组里面。虽然节点可以以面向对象的风格被动态的产生，记录和保存，我发现创建和删除对象所增加的大量时间，以及多余的管理层次减慢的整个过程的速度。但是，如果你使用数组，你需要在调用之间清理数据。这中情形你想做的最后一件事就是在寻路调用之后花点时间把一切归零，尤其是你的地图很大的时候。

我通过使用一个叫做whichList(x,y)的二维数组避免这种开销，数组的每个元素表明了节点在开启列表还是在关闭列表中。尝试寻路之后，我没有清零这个数组。取而代之的是，我在新的寻路中重置onClosedList和onOpenList的数值，每次寻路两个都+5或者类似其他数值。这种方法，算法可以安全的跳过前面寻路留下的脏数据。我还在数组中储存了诸如F,G和H的值。这样一来，我只需简单的重写任何已经存在的值而无需被清除数组的操作干扰。将数据存储在多维数组中需要更多内存，所以这里需要权衡利弊。最后，你应该使用你最得心应手的方法。

8. Dijkstra的算法：尽管A*被认为是通常最好的寻路算法(看前面的“题外话”),还是有一种另外的算法有它的可取之处-Dijkstra算法。Dijkstra算法和A*本质是相同的，只有一点不同，就是Dijkstra算法没有启发式(H值总是)。由于没有启发式，它在各个方向上平均搜索。正如你所预料，由于Dijkstra算法在找到目标前通常会探索更大的区域，所以一般会比A*更慢一些。

那么为什么要使用这种算法呢？因为有时候我们并不知道目标的位置。比如说你有一个资源采集单位，需要获取某种类型的资源若干。它可能知道几个资源区域，但是它想去最近的那个。这种情况，Dijkstra算法就比A*更适合，因为我们不知道哪个更近。用A*，我们唯一的选择是依次对每个目标许路并计算距离，然后选择最近的路径。我们寻找的目标可能会有不计其数的位置，我们只想找其中最近的，而我们并不知道它在哪里，或者不知道哪个是最近的。

转载2：

http://www.cnblogs.com/iwtwiioi/p/3889052.html

初识A*算法

　　写这篇文章的初衷是应一个网友的要求，当然我也发现现在有关人工智能的中文站点实在太少，我在这里抛砖引玉，希望大家都来热心的参与。

　　还是说正题，我先拿A*算法开刀，是因为A*在游戏中有它很典型的用法，是人工智能在游戏中的代表。

　　A*算法在人工智能中是一种典型的启发式搜索算法，为了说清楚A*算法，我看还是先说说何谓启发式算法。

一、何谓启发式搜索算法

　　在说它之前先提提状态空间搜索。状态空间搜索，如果按专业点的说法就是将问题求解过程表现为从初始状态到目标状态寻找这个路径的过程。通俗点说，就是在解一个问题时，找到一条解题的过程可以从求解的开始到问题的结果（好象并不通俗哦）。由于求解问题的过程中分枝有很多，主要是求解过程中求解条件的不确定性，不完备性造成的，使得求解的路径很多这就构成了一个图，我们说这个图就是状态空间。问题的求解实际上就是在这个图中找到一条路径可以从开始到结果。这个寻找的过程就是状态空间搜索。

　　常用的状态空间搜索有深度优先和广度优先。广度优先是从初始状态一层一层向下找，直到找到目标为止。深度优先是按照一定的顺序前查找完一个分支，再查找另一个分支，以至找到目标为止。这两种算法在数据结构书中都有描述，可以参看这些书得到更详细的解释。

　　前面说的广度和深度优先搜索有一个很大的缺陷就是他们都是在一个给定的状态空间中穷举。这在状态空间不大的情况下是很合适的算法，可是当状态空间十分大，且不预测的情况下就不可取了。他的效率实在太低，甚至不可完成。在这里就要用到启发式搜索了。

　　启发式搜索就是在状态空间中的搜索对每一个搜索的位置进行评估，得到最好的位置，再从这个位置进行搜索直到目标。这样可以省略大量无畏的搜索路径，提到了效率。在启发式搜索中，对位置的估价是十分重要的。采用了不同的估价可以有不同的效果。我们先看看估价是如何表示的。

　　启发中的估价是用估价函数表示的，如：

　　f(n) = g(n) + h(n)

　　其中f(n)是节点n的估价函数，g(n)实在状态空间中从初始节点到n节点的实际代价，h(n)是从n到目标节点最佳路径的估计代价。在这里主要是h(n)体现了搜索的启发信息，因为g(n)是已知的。如果说详细点，g(n)代表了搜索的广度的优先趋势。但是当h(n)>>g(n)时，可以省略g(n),而提高效率。这些就深了，不懂也不影响啦！我们继续看看何谓A*算法。

二、初识A*算法

　　启发式搜索其实有很多的算法，比如：局部择优搜索法、最好优先搜索法等等。当然A*也是。这些算法都使用了启发函数，但在具体的选取最佳搜索节点时的策略不同。象局部择优搜索法，就是在搜索的过程中选取“最佳节点”后舍弃其他的兄弟节点，父亲节点，而一直得搜索下去。这种搜索的结果很明显，由于舍弃了其他的节点，可能也把最好的节点都舍弃了，因为求解的最佳节点只是在该阶段的最佳并不一定是全局的最佳。最好优先就聪明多了，他在搜索时，便没有舍弃节点（除非该节点是死节点），在每一步的估价中都把当前的节点和以前的节点的估价值比较得到一个“最佳的节点”。这样可以有效的防止“最佳节点”的丢失。那么A*算法又是一种什么样的算法呢？其实A*算法也是一种最好优先的算法。只不过要加上一些约束条件罢了。由于在一些问题求解时，我们希望能够求解出状态空间搜索的最短路径，也就是用最快的方法求解问题，A*就是干这种事情的！我们先下个定义，如果一个估价函数可以找出最短的路径，我们称之为可采纳性。A*算法是一个可采纳的最好优先算法。A*算法的估价函数可表示为：

　　f'(n) = g'(n) + h'(n)

　　这里，f'(n)是估价函数，g'(n)是起点到终点的最短路径值，h'(n)是n到目标的最断路经的启发值。由于这个f'(n)其实是无法预先知道的，所以我们用前面的估价函数f(n)做近似。g(n)代替g'(n)，但g(n)>=g'(n)才可（大多数情况下都是满足的，可以不用考虑），h(n)代替h'(n)，但h(n)<=h'(n)才可（这一点特别的重要）。可以证明应用这样的估价函数是可以找到最短路径的，也就是可采纳的。我们说应用这种估价函数的最好优先算法就是A*算法。哈！你懂了吗？肯定没懂！接着看！

　　举一个例子，其实广度优先算法就是A*算法的特例。其中g(n)是节点所在的层数，h(n)=0，这种h(n)肯定小于h'(n)，所以由前述可知广度优先算法是一种可采纳的。实际也是。当然它是一种最臭的A*算法。

　　再说一个问题，就是有关h(n)启发函数的信息性。h(n)的信息性通俗点说其实就是在估计一个节点的值时的约束条件，如果信息越多或约束条件越多则排除的节点就越多，估价函数越好或说这个算法越好。这就是为什么广度优先算法的那么臭的原因了，谁叫它的h(n)=0，一点启发信息都没有。但在游戏开发中由于实时性的问题，h(n)的信息越多，它的计算量就越大，耗费的时间就越多。就应该适当的减小h(n)的信息，即减小约束条件。但算法的准确性就差了，这里就有一个平衡的问题。可难了，这就看你的了！

　　好了我的话也说得差不多了，我想你肯定是一头的雾水了，其实这是写给懂A*算法的同志看的。哈哈！你还是找一本人工智能的书仔细看看吧！我这几百字是不足以将A*算法讲清楚的。只是起到抛砖引玉的作用，希望大家热情参与嘛！

　　预知A*算法的应用，请看姊妹篇《深入A*算法》。

 

深入A*算法

深入A*算法

一、前言

　　在这里我将对A*算法的实际应用进行一定的探讨，并且举一个有关A*算法在最短路径搜索的例子。值得注意的是这里并不对A*的基本的概念作介绍，如果你还对A*算法不清楚的话，请看姊妹篇《初识A*算法》。

　　这里所举的例子是参考AMIT主页中的一个源程序，使用这个源程序时，应该遵守一定的公约。

二、A*算法的程序编写原理

　　我在《初识A*算法》中说过，A*算法是最好优先算法的一种。只是有一些约束条件而已。我们先来看看最好优先算法是如何编写的吧。

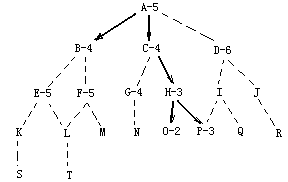
　　如图有如下的状态空间：（起始位置是A，目标位置是P，字母后的数字表示节点的估价值）

　　搜索过程中设置两个表：OPEN和CLOSED。OPEN表保存了所有已生成而未考察的节点，CLOSED表中记录已访问过的节点。算法中有一步是根据估价函数重排OPEN表。这样循环中的每一步只考虑OPEN表中状态最好的节点。具体搜索过程如下：

1）初始状态：　　　　　　　　　　　　　　　　
　OPEN=[A5]；CLOSED=[]；
2）估算A5，取得搜有子节点，并放入OPEN表中；
　OPEN=[B4，C4，D6]；CLOSED=[A5]
3）估算B4，取得搜有子节点，并放入OPEN表中；
　OPEN=[C4，E5，F5，D6]；CLOSED=[B4，A5]
4）估算C4；取得搜有子节点，并放入OPEN表中；
　OPEN=[H3，G4，E5，F5，D6]；CLOSED=[C4，B4，A5]
5）估算H3，取得搜有子节点，并放入OPEN表中；
　OPEN=[O2，P3，G4，E5，F5，D6]；CLOSED=[H3，C4，B4，A5]
6）估算O2，取得搜有子节点，并放入OPEN表中；
　OPEN=[P3，G4，E5，F5，D6]；CLOSED=[O2，H3，C4，B4，A5]
7）估算P3，已得到解；

　　看了具体的过程，再看看伪程序吧。算法的伪程序如下：

Best_First_Search()
{
　Open = [起始节点];
　Closed = [];
　while (Open表非空)
　{
　　从Open中取得一个节点X，并从OPEN表中删除。
　　if (X是目标节点)
　　{
　　　求得路径PATH；
　　　返回路径PATH；
　　}
　　for (每一个X的子节点Y)
　　{
　　　if (Y不在OPEN表和CLOSE表中)
　　　{
　　　　求Y的估价值；
　　　　并将Y插入OPEN表中；
　　　}
　　　//还没有排序
　　　else if (Y在OPEN表中)
　　　{
　　　　if (Y的估价值小于OPEN表的估价值)
　　　　　更新OPEN表中的估价值；
　　　}
　　　else //Y在CLOSE表中
　　　{
　　　　if (Y的估价值小于CLOSE表的估价值)
　　　　{
　　　　　更新CLOSE表中的估价值；
　　　　　从CLOSE表中移出节点，并放入OPEN表中；
　　　　}
　　　}
　　　将X节点插入CLOSE表中；
　　　按照估价值将OPEN表中的节点排序；
　　}//end for
　}//end while
}//end func

　　啊！伪程序出来了，写一个源程序应该不是问题了，依葫芦画瓢就可以。A*算法的程 序与此是一样的，只要注意估价函数中的g(n)的h(n)约束条件就可以了。不清楚的可以看看《初识A*算法》。好了，我们可以进入另一个重要的话题，用 A*算法实现最短路径的搜索。在此之前你最好认真的理解前面的算法。不清楚可以找我。我的Email在文章尾。

三、用A*算法实现最短路径的搜索

　　在游戏设计中，经常要涉及到最短路径的搜索，现在一个比较好的方法就是用A*算法进行设计。他的好处我们就不用管了，反正就是好！^_*

　　注意下面所说的都是以ClassAstar这个程序为蓝本，你可以在这里下载这个程序。这个程序是一个完整的工程。里面带了一个EXE文件。可以先看看。

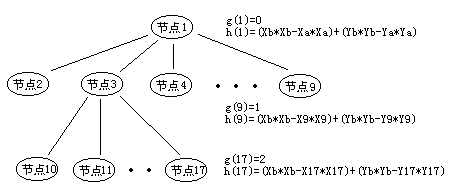
　　先复习一下，A*算法的核心是估价函数f(n)，它包括g(n)和h(n)两部 分。g(n)是已经走过的代价，h(n)是n到目标的估计代价。在这个例子中g(n)表示在状态空间从起始节点到n节点的深度，h(n)表示n节点所在地 图的位置到目标位置的直线距离。啊！一个是状态空间，一个是实际的地图，不要搞错了。再详细点说，有一个物体A，在地图上的坐标是(xa,ya)，A所要 到达的目标b的坐标是(xb,yb)。则开始搜索时，设置一个起始节点1，生成八个子节点2- 9 因为有八个方向。如图：

　　仔细看看节点1、9、17的g(n)和h(n)是怎么计算的。现在应该知道了下面 程序中的f(n)是如何计算的吧。开始讲解源程序了。其实这个程序是一个很典型的教科书似的程序，也就是说只要你看懂了上面的伪程序，这个程序是十分容易 理解的。不过他和上面的伪程序有一些的不同，我在后面会提出来。

　　先看搜索主函数：

void AstarPathfinder::FindPath(int sx, int sy, int dx, int dy)
{
    NODE *Node, *BestNode;
    int TileNumDest;
    //得到目标位置，作判断用
    TileNumDest = TileNum(sx, sy);
    //生成Open和Closed表
    OPEN = ( NODE* )calloc(1,sizeof( NODE ));
    CLOSED=( NODE* )calloc(1,sizeof( NODE ));
    //生成起始节点，并放入Open表中
    Node=( NODE* )calloc(1,sizeof( NODE ));
    Node->g = 0;
    //这是计算h值
    // should really use sqrt().
    Node->h = (dx-sx)*(dx-sx) + (dy-sy)*(dy-sy);
    //这是计算f值，即估价值
    Node->f = Node->g+Node->h;
    Node->NodeNum = TileNum(dx, dy);
    Node->x = dx; Node->y = dy;
    // make Open List point to first node
    OPEN->NextNode=Node;
    for (;;)
    {
        //从Open表中取得一个估价值最好的节点
        BestNode=ReturnBestNode();
        //如果该节点是目标节点就退出
        // if we've found the end, break and finish break;
        if (BestNode->NodeNum == TileNumDest)
        //否则生成子节点
        GenerateSuccessors(BestNode,sx,sy);
    }
    PATH = BestNode;
}

　　再看看生成子节点函数：

void AstarPathfinder::GenerateSuccessors(NODE *BestNode, int dx, int　dy)
{
    int x, y;
    //哦！依次生成八个方向的子节点，简单！
    // Upper-Left
    if ( FreeTile(x=BestNode->x-TILESIZE, y=BestNode->y-TILESIZE) )
        GenerateSucc(BestNode,x,y,dx,dy);
    // Upper
    if ( FreeTile(x=BestNode->x, y=BestNode->y-TILESIZE) )
        GenerateSucc(BestNode,x,y,dx,dy);
    // Upper-Right
    if ( FreeTile(x=BestNode->x+TILESIZE, y=BestNode->y-TILESIZE) )
        GenerateSucc(BestNode,x,y,dx,dy);
    // Right
    if ( FreeTile(x=BestNode->x+TILESIZE, y=BestNode->y) )
        GenerateSucc(BestNode,x,y,dx,dy);
    // Lower-Right
    if ( FreeTile(x=BestNode->x+TILESIZE, y=BestNode->y+TILESIZE) )
        GenerateSucc(BestNode,x,y,dx,dy);
    // Lower
    if ( FreeTile(x=BestNode->x, y=BestNode->y+TILESIZE) )
        GenerateSucc(BestNode,x,y,dx,dy);
    // Lower-Left
    if ( FreeTile(x=BestNode->x-TILESIZE, y=BestNode->y+TILESIZE) )
        GenerateSucc(BestNode,x,y,dx,dy);
    // Left
    if ( FreeTile(x=BestNode->x-TILESIZE, y=BestNode->y) )
        GenerateSucc(BestNode,x,y,dx,dy);
}        

　　看看最重要的函数：

void AstarPathfinder::GenerateSucc(NODE *BestNode,int x, int y, int dx, int dy)
{
    int g, TileNumS, c = 0;
    NODE *Old, *Successor;
    //计算子节点的 g 值
    // g(Successor)=g(BestNode)+cost of getting from BestNode to Successor
    g = BestNode->g+1;
    // identification purposes
    TileNumS = TileNum(x,y);
    //子节点再Open表中吗？
    // if equal to NULL then not in OPEN list, else it returns the Node in Old
    if ( (Old=CheckOPEN(TileNumS)) != NULL )
    {
        //若在
        for( c = 0; c < 8; c++)
        // Add Old to the list of BestNode's Children (or Successors).
            if( BestNode->Child[c] == NULL )
                break;
        BestNode->Child[c] = Old;
        //比较Open表中的估价值和当前的估价值（只要比较g值就可以了）
        // if our new g value is < Old's then reset Old's parent to point to BestNode
        if ( g < Old->g )
        {
            //当前的估价值小就更新Open表中的估价值
            Old->Parent = BestNode;
            Old->g = g;
            Old->f = g + Old->h;
        }
    }
    else
    //在Closed表中吗？
    // if equal to NULL then not in OPEN list, else it returns the Node in Old
    if ( (Old=CheckCLOSED(TileNumS)) != NULL )
    {
        //若在
        for( c = 0; c< 8; c++)
        // Add Old to the list of BestNode's Children (or Successors).
            if ( BestNode->Child[c] == NULL )
                break;
        BestNode->Child[c] = Old;
        //比较Closed表中的估价值和当前的估价值（只要比较g值就可以了）
        // if our new g value is < Old's then reset Old's parent to point to BestNode
        if ( g < Old->g )
        {
            //当前的估价值小就更新Closed表中的估价值
            Old->Parent = BestNode;
            Old->g = g;
            Old->f = g + Old->h;
            //再依次更新Old的所有子节点的估价值
            // Since we changed the g value of Old, we need
            // to propagate this new value downwards, i.e.
            // do a Depth-First traversal of the tree!
            PropagateDown(Old);
        }
    }
    //不在Open表中也不在Close表中
    else
    {
        //生成新的节点
        Successor = ( NODE* )calloc(1,sizeof( NODE ));
        Successor->Parent = BestNode;
        Successor->g = g;
        // should do sqrt(), but since we don't really
        Successor->h = (x-dx)*(x-dx) + (y-dy)*(y-dy);
        // care about the distance but just which branch looks
        Successor->f = g+Successor->h;
        // better this should suffice. Anyayz it's faster.
        Successor->x = x;
        Successor->y = y;
        Successor->NodeNum = TileNumS;
        //再插入Open表中，同时排序。
        // Insert Successor on OPEN list wrt f
        Insert(Successor);
        for( c =0; c < 8; c++)
        // Add Old to the list of BestNode's Children (or Successors).
        if ( BestNode->Child[c] == NULL )
            break;
        BestNode->Child[c] = Successor;
    }
}

　　哈哈！A*算法我懂了！当然，我希望你有这样的感觉！不过我还要再说几句。仔细看 看这个程序，你会发现，这个程序和我前面说的伪程序有一些不同，在GenerateSucc函数中，当子节点在Closed表中时，没有将子节点从 Closed表中删除并放入Open表中。而是直接的重新的计算该节点的所有子节点的估价值（用PropagateDown函数）。这样可以快一些！另当 子节点在Open表和Closed表中时，重新的计算估价值后，没有重新的对Open表中的节点排序，我有些想不通，为什么不排呢？:-(，会不会是一个 小小的BUG。你知道告诉我好吗？

　　好了！主要的内容都讲完了，还是完整仔细的看看源程序吧！希望我所的对你有一点帮助，一点点也可以。如果你对文章中的观点有异议或有更好的解释都告诉我。我的email在文章最后！

 

 

1085: [SCOI2005]骑士精神

Time Limit: 10 Sec  Memory Limit: 162 MB
Submit: 1712  Solved: 937
[Submit][Status][Discuss]

Description

　　在一个5×5的棋盘上有12个白色的骑士和12个黑色的骑士， 且有一个空位。在任何时候一个骑士都能按照骑
士的走法（它可以走到和它横坐标相差为1，纵坐标相差为2或者横坐标相差为2，纵坐标相差为1的格子）移动到空
位上。 给定一个初始的棋盘，怎样才能经过移动变成如下目标棋盘： 为了体现出骑士精神，他们必须以最少的步
数完成任务。

Input

　　第一行有一个正整数T(T<=10)，表示一共有N组数据。接下来有T个5×5的矩阵，0表示白色骑士，1表示黑色骑
士，*表示空位。两组数据之间没有空行。

Output

　　对于每组数据都输出一行。如果能在15步以内（包括15步）到达目标状态，则输出步数，否则输出－1。

Sample Input

2
10110
01*11
10111
01001
00000
01011
110*1
01110
01010
00100

Sample Output

7
-1

/*
这个题目的具体算法是：IDA*算法，
（因为这个题目已经说了最多不超过15步），
所以我们可以用“迭代加深搜索+A*搜索”，
叫做“IDA*算法”（估计函数就相当于给迭代剪枝了）。
*/

 

#include<cstring>
#include<iostream>
using namespace std;
#include<cstdio>
int T;
char mapp[6][6];
int xx[9]={0,-1,-2,-2,-1,1,1,2,2};
int yy[9]={0,-2,-1,1,2,-2,2,1,-1};
void build_ma()
{
    mapp[1][1]=mapp[1][2]=mapp[1][3]=mapp[1][4]=mapp[1][5]=mapp[2][2]=mapp[2][3]=mapp[2][4]=mapp[2][5]=mapp[3][4]=mapp[3][5]=mapp[4][5]='1';
    mapp[2][1]=mapp[3][1]=mapp[3][2]=mapp[4][1]=mapp[4][2]=mapp[4][3]=mapp[4][4]=mapp[5][1]=mapp[5][2]=mapp[5][3]=mapp[5][4]=mapp[5][5]='0';
}
/*int h(char beginn[6][6])
{
    int ret=0;
    for(int i=1;i<=5;++i)
      for(int j=1;j<=5;++j)
      if(beginn[i][j]!=mapp[i][j]) ret++;
    return ret;
}*/
/*一开始h函数是上面的写法，结果错了，估价h必须要小于等于真实的，就是不在对应位置上的骑士数目，不包括“*”，这样有可能大于真实值了。*/
int h(char beginn[6][6])
{
    int ret=0;
    for(int i=1;i<=5;++i)
      for(int j=1;j<=5;++j)
      if((i!=3||j!=3)&&beginn[i][j]!=mapp[i][j]) ret++;
    return ret;
}
void dfs(char beginn[6][6],int step,int &ans)
{
    if(step+h(beginn)>=ans) return;
    else if(!h(beginn))
    {
        ans=min(step,ans);//return;
    }
    int x=0,y=0;
    for(int i=1;i<=5;++i)
    {
     for(int j=1;j<=5;++j)
      if(beginn[i][j]=='*')
      {
          x=i;y=j;break;
      }
      if(x&&y)break;
    }
    for(int i=1;i<=8;++i)
    {
        int x1=x+xx[i],y1=y+yy[i];
        if(x1>5||x1<1||y1>5||y1<1) continue;
        char b[6][6];
        for(int j=1;j<=5;++j)
          for(int k=1;k<=5;++k)
          b[j][k]=beginn[j][k];
        swap(b[x1][y1],b[x][y]);
        dfs(b,step+1,ans);
    }
}
int main()
{
    build_ma();
    scanf("%d",&T);
    for(int i=1;i<=T;++i)
    {
        char beginn[6][6];
        for(int j=1;j<=5;++j)
           scanf("%s",beginn[j]+1);
        int ans=16;
        dfs(beginn,0,ans);
        if(ans>=16) printf("-1\n");
        else printf("%d\n",ans);    
    }
    return 0;
}