线段树练习两题
1.线段树练习1:

输入:n
(n个数)
k
(k 行) 1 k p 将a[k]改为p
2 l r 区间查询
1 /* 2 一开始看错题目了,没有看到要求:“l<=j<=i<=r”的条件 3 这是错误代码: 4 */ 5 /*错误代码: 6 */ 7 #include<iostream> 8 using namespace std; 9 #include<cstdio> 10 #define N 10000 11 #define mid ((l+r)>>1) 12 #define lch (2*k) 13 #define rch ((2*k)+1) 14 struct Jg{ 15 int firs,secn; 16 }; 17 struct Tree{ 18 int minn,maxx; 19 }tree[N<<2]; 20 int n,k,sum[N]; 21 inline int read() 22 { 23 int ret=0,ff=1; 24 char s=getchar(); 25 while(s<'0'||s>'9') 26 { 27 if(s=='-') ff=-1; 28 s=getchar(); 29 } 30 while(s>='0'&&s<='9') 31 { 32 ret=ret*10+s-'0'; 33 s=getchar(); 34 } 35 return ret*ff; 36 } 37 void input() 38 { 39 n=read(); 40 for(int i=1;i<=n;++i) 41 sum[i]=read(); 42 } 43 void update(int k) 44 { 45 tree[k].maxx=max(tree[lch].maxx,tree[rch].maxx); 46 tree[k].minn=min(tree[lch].minn,tree[rch].minn); 47 return; 48 } 49 void build(int k,int l,int r) 50 { 51 if(l==r) 52 { 53 tree[k].minn=tree[k].maxx=sum[l]; 54 return; 55 } 56 build(lch,l,mid); 57 build(rch,mid+1,r); 58 update(k); 59 } 60 void change(int k,int l,int r,int pos,int z) 61 { 62 if(l==r) 63 { 64 tree[k].maxx=tree[k].minn=z; 65 return ; 66 } 67 if(pos<=mid) change(lch,l,mid,pos,z); 68 else change(rch,mid+1,r,pos,z); 69 update(k); 70 } 71 Jg query(int k,int l,int r,int x,int y) 72 { 73 if(x<=l&&r<=y) 74 { 75 return Jg{tree[k].maxx,tree[k].minn};/*这里是必须要返回最大值和最小值的,因为可能都有用,不能只返回max-min,这样是不对的。*/ 76 } 77 int maxxx=-1000000000,minnn=1000000000; 78 Jg A={maxxx,minnn},B={maxxx,minnn}; 79 if(x<=mid) 80 A=query(lch,l,mid,x,y); 81 if(y>mid) 82 B=query(rch,mid+1,r,x,y); 83 return Jg{max(A.firs,B.firs),min(A.secn,B.secn)}; 84 } 85 int main() 86 { 87 input(); 88 build(1,1,n); 89 k=read(); 90 int x,y,z; 91 for(int i=1;i<=k;++i) 92 { 93 x=read();y=read();z=read(); 94 if(x==1) 95 { 96 change(1,1,n,y,z); 97 } 98 else { 99 Jg P=query(1,1,n,y,z); 100 printf("%d\n",P.firs-P.secn); 101 } 102 } 103 return 0; 104 }
解析:

1 /*正确代码:值得注意的一点:就是每个区间初始的ans值必须是最小的,叶子节点上的ans不能是自身,这样是没有正确意义的。 2 */ 3 #include<iostream> 4 using namespace std; 5 #include<cstdio> 6 #define N 10000 7 #define mid ((l+r)>>1) 8 #define lch (2*k) 9 #define rch ((2*k)+1) 10 struct Jg{ 11 int firs,secn,thir; 12 }; 13 struct Tree{ 14 int minn,maxx,ans; 15 }tree[N<<2]; 16 int n,k,sum[N]; 17 inline int read() 18 { 19 int ret=0,ff=1; 20 char s=getchar(); 21 while(s<'0'||s>'9') 22 { 23 if(s=='-') ff=-1; 24 s=getchar(); 25 } 26 while(s>='0'&&s<='9') 27 { 28 ret=ret*10+s-'0'; 29 s=getchar(); 30 } 31 return ret*ff; 32 } 33 void input() 34 { 35 n=read(); 36 for(int i=1;i<=n;++i) 37 sum[i]=read(); 38 } 39 void update(int k) 40 { 41 tree[k].maxx=max(tree[lch].maxx,tree[rch].maxx); 42 tree[k].minn=min(tree[lch].minn,tree[rch].minn); 43 tree[k].ans=max(max(tree[k].ans,tree[rch].maxx-tree[k].minn),max(tree[lch].ans,tree[rch].ans)); 44 return; 45 } 46 void build(int k,int l,int r) 47 { 48 if(l==r) 49 { 50 tree[k].minn=tree[k].maxx=sum[l]; 51 tree[k].ans=-1000000000; 52 return; 53 } 54 build(lch,l,mid); 55 build(rch,mid+1,r); 56 update(k); 57 } 58 void change(int k,int l,int r,int pos,int z) 59 { 60 if(l==r) 61 { 62 tree[k].maxx=tree[k].minn=z; 63 return; 64 } 65 if(pos<=mid) change(lch,l,mid,pos,z); 66 else change(rch,mid+1,r,pos,z); 67 update(k); 68 } 69 Jg query(int k,int l,int r,int x,int y) 70 { 71 if(x<=l&&r<=y) 72 { 73 return Jg{tree[k].maxx,tree[k].minn,tree[k].ans}; 74 } 75 int maxxx=-1000000000,minnn=1000000000; 76 Jg A={maxxx,minnn,maxxx},B={maxxx,minnn,maxxx}; 77 if(x<=mid) 78 A=query(lch,l,mid,x,y); 79 if(y>mid) 80 B=query(rch,mid+1,r,x,y); 81 return Jg{max(A.firs,B.firs),min(A.secn,B.secn),max(B.firs-A.secn,max(A.thir,B.thir))}; 82 } 83 int main() 84 { 85 input(); 86 build(1,1,n); 87 k=read(); 88 int x,y,z; 89 for(int i=1;i<=k;++i) 90 { 91 x=read();y=read();z=read(); 92 if(x==1) 93 { 94 change(1,1,n,y,z); 95 } 96 else { 97 Jg P=query(1,1,n,y,z); 98 printf("%d\n",P.thir); 99 } 100 } 101 return 0; 102 }
2.线段树练习2:布尔数组

输入:
1 输入:n 2 (n个数) 3 k 4 (k 行) 1 k p 将a[k]改为p 5 2 l r 区间查询
解析:

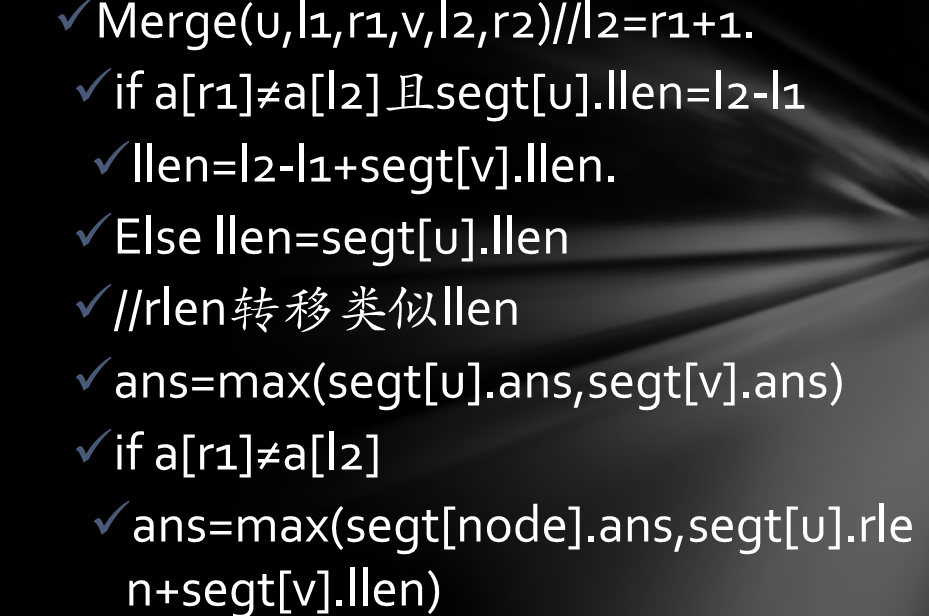
代码:
1 /* 2 这道题目的关键就是这个递推关系 3 */ 4 #define N 100000 5 #include<iostream> 6 #include<cstdio> 7 #define lch (k<<1) 8 #define rch ((k<<1)+1) 9 #define mid ((l+r)>>1) 10 using namespace std; 11 struct Jg{ 12 int llen,rlen,ans; 13 }; 14 struct Tree{ 15 int llen,rlen,ans; 16 }segt[N<<2]; 17 int n,k,sum[N]; 18 void input() 19 { 20 scanf("%d",&n); 21 for(int i=1;i<=n;++i) 22 scanf("%d",&sum[i]); 23 } 24 void update(int k,int l,int r) 25 { 26 if(sum[mid]!=sum[mid+1]&&segt[lch].llen==mid+1-l) 27 segt[k].llen=mid+1-l+segt[rch].llen; 28 else segt[k].llen=segt[lch].llen; 29 if(sum[mid]!=sum[mid+1]&&segt[rch].rlen==r-mid) 30 segt[k].rlen=r-mid+segt[lch].rlen; 31 else segt[k].rlen=segt[rch].rlen; 32 segt[k].ans=max(segt[lch].ans,segt[rch].ans); 33 if(sum[mid]!=sum[mid+1]) 34 segt[k].ans=max(segt[k].ans,segt[rch].llen+segt[lch].rlen); 35 36 } 37 void build_segt(int k,int l,int r) 38 { 39 if(l==r) 40 { 41 segt[k].ans=segt[k].llen=segt[k].rlen=1; 42 return; 43 } 44 build_segt(lch,l,mid); 45 build_segt(rch,mid+1,r); 46 update(k,l,r); 47 } 48 void change(int k,int l,int r,int pos,int z) 49 { 50 if(l==r) 51 { 52 sum[pos]=z; 53 return; 54 } 55 if(pos<=mid) 56 change(lch,l,mid,pos,z); 57 else change(rch,mid+1,r,pos,z); 58 update(k,l,r); 59 } 60 Jg query(int k,int l,int r,int x,int y) 61 { 62 if(x<=l&&r<=y) 63 { 64 return Jg{segt[k].llen,segt[k].rlen,segt[k].ans}; 65 } 66 if(x>mid) 67 return query(rch,mid+1,r,x,y); 68 if(y<=mid) return query(lch,l,mid,x,y); 69 Jg B=query(rch,mid+1,r,x,y); 70 Jg A=query(lch,l,mid,x,y); 71 int llen,rlen,ans;/*注意这里的A,B区间不一定是规则的区间,有可能是几个区间拼凑在一起,但是一定有A与B相邻*/ 72 /*这道题目的关键就是这个递推关系*/ 73 if(sum[mid]!=sum[mid+1]&&A.llen==mid+1-x) 74 llen=mid+1-l+B.llen; 75 else llen=A.llen; 76 if(sum[mid]!=sum[mid+1]&&B.rlen==r-mid) 77 rlen=r-mid+A.rlen; 78 else rlen=B.rlen; 79 ans=max(A.ans,B.ans); 80 if(sum[mid]!=sum[mid+1]) 81 ans=max(ans,B.llen+A.rlen); 82 return Jg{llen,rlen,ans}; 83 } 84 int main() 85 { 86 input(); 87 build_segt(1,1,n); 88 scanf("%d",&k); 89 int x,y,z; 90 for(int i=1;i<=n;++i) 91 { 92 scanf("%d%d%d",&x,&y,&z); 93 if(x==1) 94 { 95 change(1,1,n,y,z); 96 } 97 else { 98 Jg P=query(1,1,n,y,z); 99 printf("%d\n",P.ans); 100 } 101 } 102 return 0; 103 }



