模型--排队论模型

排队论模型

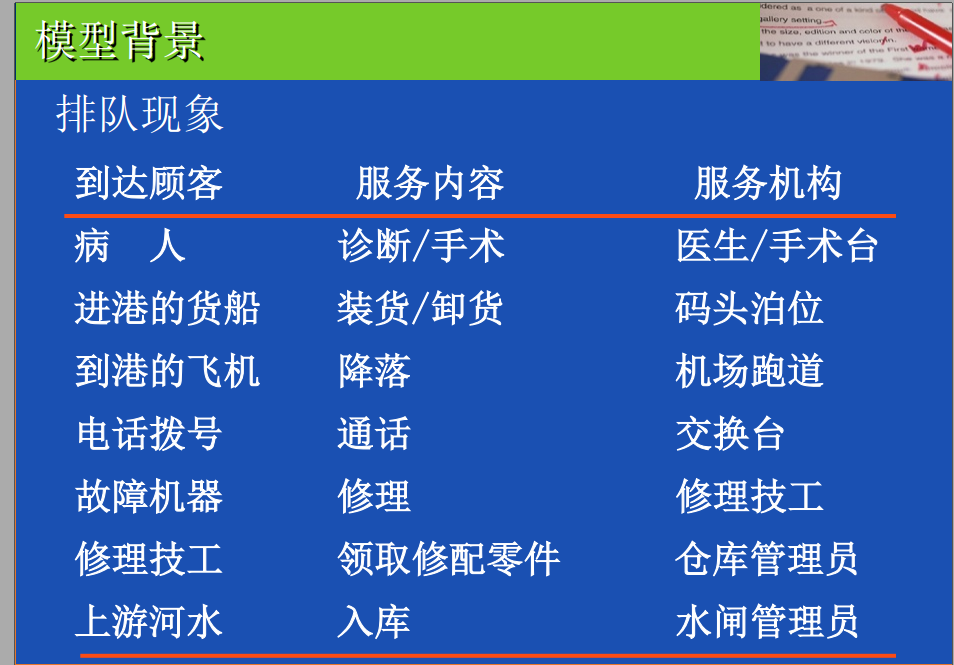
如何处理用户呼叫数量和电话线路数的关系

模型介绍

顾客的到达和服务时间都有随机性
排队过程通常是一个随机过程，所以排队论又称为"随机服务系统模型"

排队服务过程

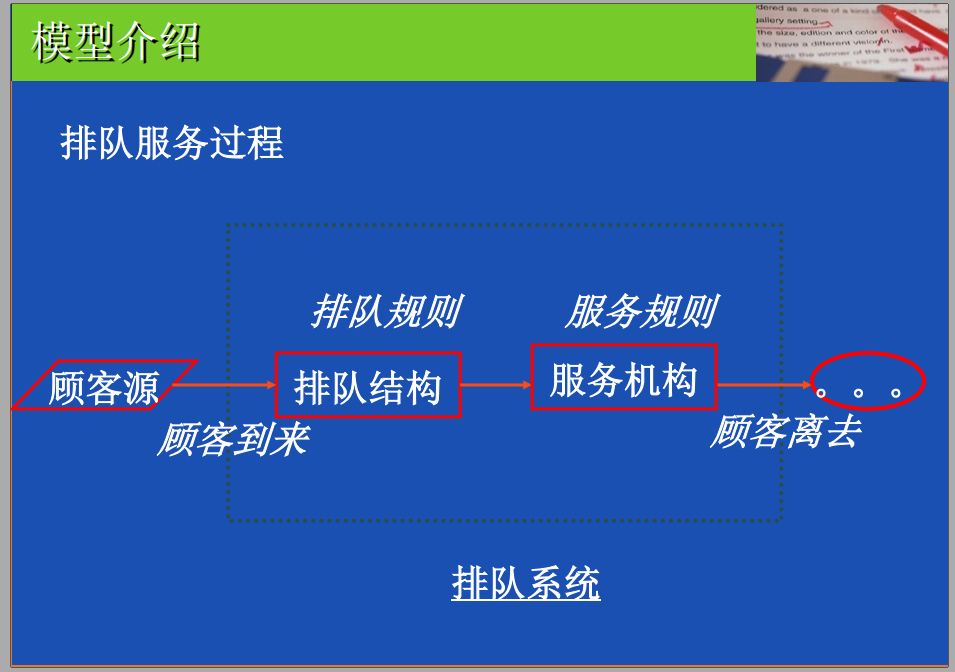
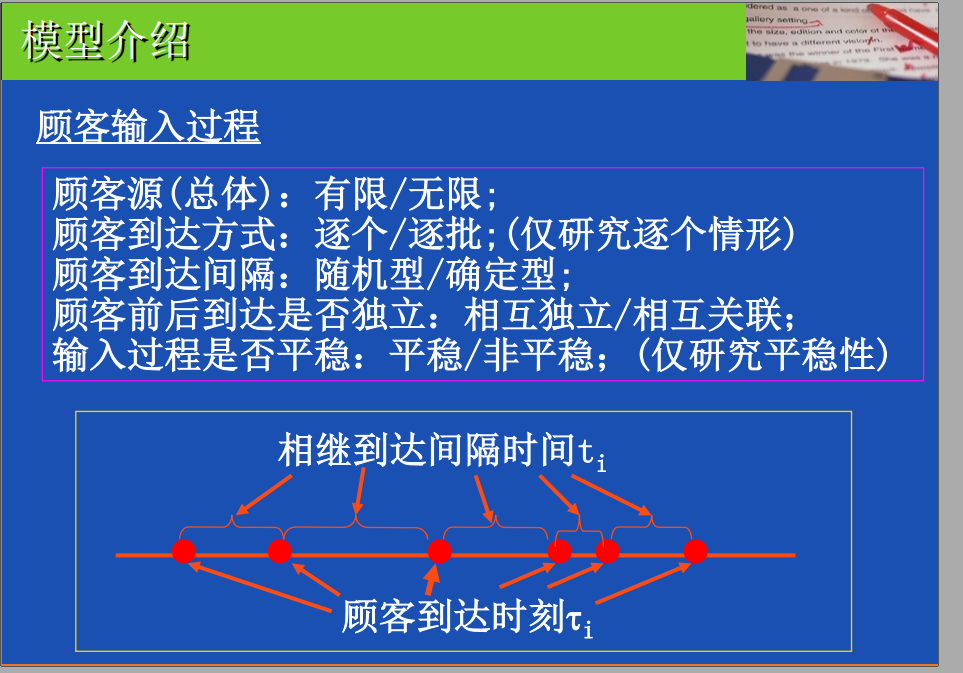
用户输入的情况

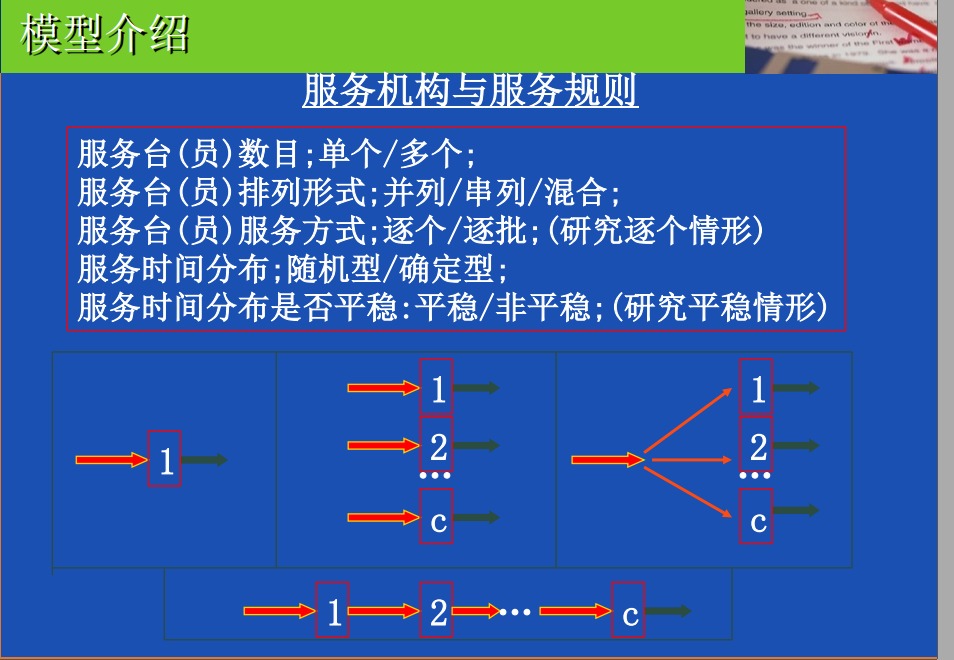
排队结构和排队规则

参数介绍

稳态概率长时间后 人数概率不再随着时间变化 新店开业的概率和长时间的不一样

评价指标，用来评价排队系统的优劣

队长: 人数的期望
排队长: 等待人数的期望

逗留时间: 一个顾客在系统总时间的期望 = 逗留时间 + 服务时间
等待时间: 一个顾客等待时间的期望

忙期:指服务机构由一个空闲时间到另一个空闲时间的 时间长度
忙期服务量: 一个忙期内系统的平均完成顾客数
损失率: 指顾客到达排排队系统 未接收服务离去的概率
服务强度： p = 入/su

用户的到达时间 可以使用泊松分布来模拟

单服务台负指数分布 M/M/1排队系统

条件:

模型计算

模型举例

入: 每小时到达人数 u: 每小时可服务人数

稳态概率 == 1-服务强度

Ls 队长
Lq 排队长
Ws 平均逗留时间(总时间) Ws = Wq + 服务时间
Wq 平均等候时间

多服务台单队模型 M/M/S S个服务台

模型计算
P 的角标是 当前总人数 为0是计算当前没有人的概率

N >= S代表了需要排队的概率

案例分析

利用上面的公式：
1. 计算了每个工作台服务强度
2. 计算了没有人的概率
3. 计算了排队长
4. 计算了队长
5. 计算了逗留时间
6. 计算了排队时间
7. 计算必须等待的概率 及每个工作台都被占满

案例分析

由题目可知:
本模型属于 MMS模型
S = 3，入:每小时到达人数 0.9 * 60 u：每小时可服务人数 0.4 * 60
p = 入/u = 2.25 p* = 2.25/3 = 3/4 < 1 p*工作强度
P0(一个人也没有） = 0.0748
排队长计算: Lq = 1.7
队长计算 Ls = 3.95
排队时间 Wq = 1.89
逗留时间 Wq = 4.39
等待的概率 Pn>=3 = 0.57